Самоорганизация в неравновесных системах

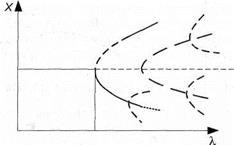
Рассмотрим простую симметричную бифуркацию, приведенную на рис. 5. Выясним, как возникает самоорганизация и какие процессы происходят, когда ее порог оказывается превзойденным.

В равновесном или слабо равновесном состоянии существует лишь одно однородное стационарное состояние А без какой-либо упорядоченности. Пусть X — некоторая главная переменная, например концентрация одного из исходных веществ. Рассмотрим, как изменяется состояние системы с возрастанием значения управляющего параметра λ (этим управляющим параметром может быть концентрация другого вещества, от которого зависит ход реакции). При некотором значении λ = λ_с система достигает порога устойчивости. Обычно данное критическое значение называют точкой биффуркации. В точке В однородное стационарное хаотическое термодинамическое состояние становится неустойчивым относительно флуктуации. При переходе через критическое состояние λ_с существуют три coстояния, в которых может находиться система: два устойчивых (С и D) и одно неустойчивое (Е). Эта ситуация напоминает бегуна, который, выбежав из дома, достиг пересечения трех дорог. Прямая дорога продолжается через шаткий мостик. Если бегун продолжит путь через мостик, он может потерять устойчивость и упасть на одну из двух твердых дорог.

Рис. 5. Простая симметричная бифуркация

Возникает естественный вопрос,: по какому пути пойдет дальнейшее развитие системы после того, как она достигла точки бифуркации? У системы есть выбор: она может отдать предпочтение одной из двух возможностей самоорганизации, соответствующих двум неравномерным распределениям концентрации X в пространстве, определяемых ветвями С и D бифуркационной диаграммы.

Одно из этих пространственных распределений зеркально симметрично другому. Каким образом система выбирает между правой и левой ветвями? В этом выборе неизбежно присутствует элемент случайности. Уравнения не в состоянии предсказать, по какой траектории пойдет эволюция системы. Мы сталкиваемся со случайными явлениями, подобными исходу бросания игральной кости или монеты. Можно ожидать, что в половине случаев система окажется в одном положении, а в половине – в другом. Теперь можно предположительно ответить на вопрос: почему в живом нарушена симметрия? Все молекулы белка, ДНК, сахаров и т.д. закручены в левую сторону. Ответ таков: диссимметрия обусловлена единичным случайным событием. После того, как выбор сделан, вступают в действие автокаталитические процессы, и левосторонняя структура порождает новые, только левосторонние структуры.

На рис. 6 показана система, которая может находиться в большом числе устойчивых и неустойчивых состояний.

Таким образом, в сильно неравновесных системах процессы самоорганизации сводятся к тонкому взаимодействию между случайностью и необходимостью, между флуктуациями и детерминистскими иконами. Вблизи точек бифуркации основную роль играют флуктуации или случайные элементы, тогда как в интервалах между точками бифуркаций доминируют детерминистские закономерности.

Рис. 6. Устойчивые и неустойчивые состояния системы

Следует особо подчеркнуть различие между равновесным (статистическим) хаосом, который может вызвать лишь небольшие отклонения-флуктуации от состояния равновесия, и динамическим хаосом и неравновесных системах, обладающих значительным избытком свободной энергии. Этот динамический созидающий хаос и служит источником всего того порядка, который мы наблюдаем в окружающем нас мире неживой и живой природы. Так, жизнь на Земле зародилась в сильно неравновесной среде, а возникшие организмы стали жить и эволюционировать, потребляя свободную энергию, поступающую к нам извне (в конечном счете, энергию Солнца).

В заключение подведем некоторые итоги.

Самоорганизация — это процесс, в ходе которого создается, воспроизводится или совершенствуется организация сложной динамической системы. Процессы самоорганизации могут иметь место только в системах, обладающих высоким уровнем сложности и большим количеством элементов, связи между которыми имеют не жесткий, а вероятностный характер. Основные свойства самоорганизующих систем — открытость, нелинейность, диссипативность. Теория самоорганизации имеет дело с открытыми нелинейными диссипативными системами, далекими от равновесия.

Свойства самоорганизации обнаруживают объекты самой различной природы: живая клетка, организм, биологическая популяция, биогеоценоз, человеческий коллектив и т.д. Процессы самоорганизации осуществляются за счет перестройки существующих и образования новых связей между элементами системы. Отличительная особенность процессов самоорганизации – их целенаправленный, но вместе с тем и естественный, спонтанный характер: эти процессы протекают при взаимодействии системы с окружающей средой, в той или иной мере автономны и относительно независимы от нее.

Поиск по сайту: