 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Параметри розподілу випадкових похибок
Числові характеристики випадкових похибок Математичне сподівання М[х] визначається як початковий момент першого порядку кривої розподілу:
Вираз для математичного сподівання похибки вимірювань є таким:
Cистематична похибка визначається як відхилення математичного сподівання результатів спостережень від істинного значення вимірюваної величини:
а випадкова похибка - це різниця між результатом однократногоспостереження і математичним сподіванням результатів:
(7.14) для кожного однократного спостереження, істинне значення вимірюваної величини визначається таким чином:
В загальному випадку, коли в результаті однократного спостереження невідомі обидві складові похибки вимірювання, результат вимірювання може бути представлений тільки в такому вигляді:
Параметри розподілу випадкових похибок Початковим моментом r-го порядку випадкової величини х є число, яке визначається таким чином:
яке ще можна назвати математичним сподіванням r-ої степені випадкової величини х. Найчастіше як параметр розподілу випадкових величин використовується початковий момент першого порядку
який називається математичним сподіванням випадкової величини. Для дискретної випадкової величини математичне сподівання (вибірковий початковий момент першого порядку) визначається так:
де В практиці визначення параметрів розподілу в деяких випадках використовують початковий момент другого порядку
який для дискретних величин має назву вибіркового моменту другого порядку і який визначають таким чином:
Початкові моменти вищих порядків практично не використовуються для характеристики розподілу випадкових величин. Для вивчення розподілу випадкових величин користуються рядом числових характеристик: міри положення і міри розсіювання. Центральним моментом k-гo порядку (k-им центральним моментом) випадкової величини х називається математичне сподівання k-ої степені її відхилення від математичного сподівання М[х]:
Перший центральний момент завжди дорівнює нулю:
В практиці визначення параметрів розподілу широко використовується центральний момент другого порядку, який ще називається дисперсією:
Для дискретних величин вибірковий центральний момент другого порядку визначають так:
Зa допомогою середнього квадратичного відхилення у можна оцінити ймовірність того, що при однократному спостереженні випадкова похибка Δ по абсолютному значенню не буде більшою від деякого наперед заданого значення ε . Це можна здійснити за допомогою нерівності П.Чебишева, яка має такий вигляд:
Допустимо, наприклад, що
Дисперсією називається математичне сподівання квадрату відхилення випадкової величини від математичного сподівання цієї величини. Дисперсія є характеристикою розсіювання значень результатів спостережень відносно математичного сподівання М[х]. Однак дисперсія є незручною для оцінки розсіювання як міра розсіювання, так як має розмірність квадрату випадкової величини, міру розсіювання значень відносно математичного сподівання використовують середнє квадратичне відхилення (СКВ) σ, за яке приймають додатне значення кореня квадратного від дисперсії тобто
Третій центральний момент т3, розраховується таким чином:
а для дискретної випадкової величини вибірковий центральний момент третього порядку визначають так:
використовують для оцінки асиметрії кривої розподілу за допомогою коефіцієнта асиметрії
Центральний момент четвертого порядку, визначається таким чином:
а для дискретної випадкової величини так:
використовують для оцінки плосковершинності або гостровершинності кривої розподілу за допомогою коефіцієнта ексцесу, який в свою чергу розраховують так:
Для нормального закону розподілу keкс=0, для гостровершинної кривої розподілу keкс>0, а для плосковершинної keкс<0 (рис. 7.5). Між центральними і початковими моментами є такі залежності, які мають практичне застосування:
Рис 7.4 Залежність форми кривих розподілу від коефіцієнтаасиметрії Рис. 7.5. Залежність форми кривої розподілувід коефіцієнта ексцесу Закон розподілу суми незалежних випадкових величин Зміна форми законів розподілу при утворенні композиції показана на рис. 7-2.
Поиск по сайту: |
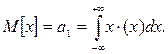 (7.10)
(7.10)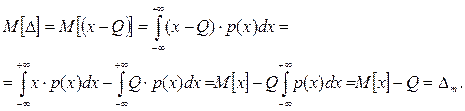 (7.11)
(7.11)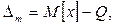 (7.12)
(7.12)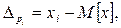 (7.13)
(7.13) (7.14)
(7.14)
 (7.14)
(7.14) (7.15)
(7.15)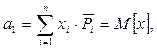 (3.16)
(3.16) – ймовірність появи випадкового значення хі яку визначають як 1/п, якщо п-загальна кількість спостережень, або як відношення кількості однакових спостережень в кожній із п таких груп до загальної кількості спостережень.
– ймовірність появи випадкового значення хі яку визначають як 1/п, якщо п-загальна кількість спостережень, або як відношення кількості однакових спостережень в кожній із п таких груп до загальної кількості спостережень.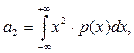 (7.17)
(7.17) (7.18)
(7.18)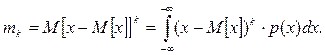 (7.19)
(7.19)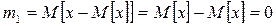
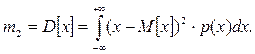 (7.20)
(7.20) (7.21).
(7.21). (3.26)
(3.26)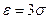 . Тоді ймовірність того, що при однократному спостереженні випадкова похибка не буде більшою від
. Тоді ймовірність того, що при однократному спостереженні випадкова похибка не буде більшою від  , буде такою:
, буде такою:
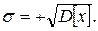
 (7.22)
(7.22) (7.23)
(7.23) (7.24)
(7.24) (7.25)
(7.25) (7.26)
(7.26) (7.27)
(7.27) (7.28)
(7.28) 

 , що мають розподіли p1(х) і p2(х), називається композицієюі виражається інтегралом згортки:
, що мають розподіли p1(х) і p2(х), називається композицієюі виражається інтегралом згортки: 
