 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение площадей аналитическим способом по результатам измерений на местности. Точность вычисления площадей аналитическим способомСтр 1 из 2Следующая ⇒
Тема 3.1. Способы определения площадей Характеристика способов определения площадей землевладений, контуров угодий Составление различного рода проектов, связанных с использованием земельной территории, изучение ее природных богатств, учет и инвентаризация земель требуют определения площадей. В зависимости от хозяйственного назначения участков и массивов, их размеров, конфигурации и вытянутости, наличия планово-картографического материала, топографических условий местности применяются следующие способы определения площадей. Аналитический, когда площадь вычисляется по результатам измерений линий и углов на местности или по их функциям – координатам вершин фигур. Графический - площади вычисляется по результатам измерений линий и углов (транспортиром) или по координатам точек на плане (карте). Механический – площади определяются на плане при помощи специальных приборов (планиметров, картометров) и приспособлений (палеток, ротометров и др..). Иногда эти способы применяют комбинированно; например, часть линейных величин для вычисления площади измеряют на плане, а часть берут из результатов измерений на местности, или при вычислении площади по координатам для одних точек принимают вычисленные (аналитические) значения координат по результатам измерений на местности, а для других точек координаты получают измерением на плане (графические). Наиболее точным является аналитический способ, так как на точность вычисления площади этим способом влияют только погрешности измерений на местности. Способ применяют для вычисления площадей землепользований, полей севооборотов, когда по границам их проложены теодолитные ходы и полигоны, а так же при обмере участков. Менее точен графический способ, так как помимо погрешностей измерений на местности на точность вычисленной площади влияют погрешности составления плана и определения площади по плану. Способ применяют для определения площадей землепользований, полей севооборотов и контуров угодий, ограниченных ломаными линиями, при этом, чем меньше площадь участка, тем с большей относительной погрешностью определяется его площадь, для больших площадей точность этого способа приближается к точности, получаемой аналитическим способом. Наименее точным является механический способ. Определение площадей аналитическим способом по результатам измерений на местности. Точность вычисления площадей аналитическим способом Для измерения площадей участков по результатам измерения линий и углов на местности применяют формулы геометрии, тригонометрии и аналитической геометрии. Рассмотрим наиболее употребительные из них. Для учета площадей занятых строениями, усадьбами, площадей вспашки, посева, участки разбивают на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции. Площади участков определяют как суммы площадей отдельных фигур, вычисляемых по линейным элементам (высотам и основаниям) по общеизвестным формулам геометрии. При учете вспашки, посева, уборки урожая площади определяют также по длине маршрута агрегата и ширине его захвата. Если по границам участка проложен теодолитный ход, то площадь всего участка или его части можно вычислить по следующим формулам: Треугольник (рис.3.1, а). Определим его площадь по двум сторонам S1 и S 2 и углу β2, заключенному между ними. Из рисунка видим, что
но
Подставив значение h в (3.1) получим
Рисунок 3.1 – Схемы определения площадей геометрических фигур
Четырехугольник. Зная четыре стороны S1, S 2, S3, S 4 и два противоположных угла β2 и β4 (рис.3.1,б), на основании формулы (3.2) получим
Если в четырехугольнике известны три стороны S1, S 2, S3 и два угла β2 и β3, заключенные между этими сторонами (рис.3.1, в), то площадь можно вычислить по формуле
Пятиугольник (3.1, г). По пяти сторонам и трем углам β2, β4, β5 на основании формул (3.2) и (3.4) получим
Такого же вида формулы можно получить для любого n - угольника, только с увеличением числа вершин n прогрессивно увеличивается количество слагаемых в формуле, поэтому при n >6 целесообразно вычислять площади по координатам вершин полигона, пользуясь формулами:
и
Чтобы площадь получилась положительной, номера точек полигона записывают в столбец ведомости всегда по ходу часовой стрелки. Число произведений в сумме равно числу точек. Если площадь фигуры вычисляется по результатам измерений на местности, то точность вычисления площади можно рассчитать пользуясь теорией погрешности некоррелированных измерений
Такую же формулу получим и для определения точности вычисления площади прямоугольника, параллелограмма и трапеции, у которой измеряется высота и средняя линия. Если приближенно считать, что измерение линий на местности производится с относительной погрешностью
Поиск по сайту: |
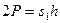 (3.1)
(3.1) .
. (3.2)
(3.2)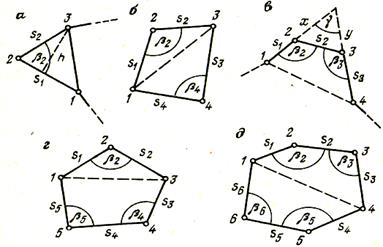
 (3.3)
(3.3)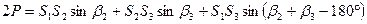 . (3.4)
. (3.4) . (3.5)
. (3.5) ,
,  (3.6)
(3.6) .
.  . (3.8)
. (3.8) , то
, то  ,
, 