 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Последовательность расчета режима трансформатора
1.Расчет токов и напряжений для номинального режима и опытов холостого хода и короткого замыкания: - токи и напряжения
2. Параметры схемы замещения - полная Т-образная схема замещения
Рисунок 2.1 - Полная электрическая схема замещения приведенного трансформатора - параметры схемы замещения
3. Расчет номинального режима трансформатора по полной схеме замещения символическим методом при заданном φ2 - сопротивления нагрузки
- сопротивления вторичной цепи
- общее сопротивление вторичной цепи и ветви намагничивания
- общее сопротивление схемы замещения
- ток первичной обмотки
- ЭДС в обмотках
- приведенный ток вторичной обмотки
- приведенное и реальное напряжения на нагрузке
- падение напряжения при работе трансформатора в номинальном режиме
4. Построение полной векторной диаграммы (рисунок 2.2) 4.1. В произвольном направлении, например, вправо от точки «0» откладывается вектор магнитного потока 4.2. С отставанием от вектора 4.3. Вектор тока холостого хода
4.4. Ток во вторичной цепи I′2 определяется из соотношения
где и отстает от вектора ЭДС на угол ψ2
4.5. Вектор напряжения на нагрузке
Таким образом, из конца вектора
Рисунок 2.2 – Полная векторная диаграмма приведенного трансформатора
4.6. Положение и величину тока
Для этого к концу вектора 4.7. Построение вектора
При этом векторы падения напряжения 4.8. Угол φ1 определяет фазовый сдвиг между напряжением
5. Построение упрощенной векторной диаграммы трансформатора (рисунок 2.4) Упрощенная векторная диаграмма является отражением упрощенной схемы замещения (рисунок 2.3) и графическим решением уравнения электрического равновесия
Рисунок 2.3 – Упрощенная схема замещения приведенного трансформатора
Порядок построения 5.1. От исходной точки «0» в произвольном направлении (например, вверх) откладывается вектор 5.2. Под углом φ2к вектору тока в сторону опережения (для активно-индуктивной нагрузки) проводится направление вектора напряжения - 5.3. В масштабе напряжения строится прямоугольный треугольник АВС со сторонами АВ=I1нxk, ВС=I1нrk, АС=I1нZk, называемый треугольником короткого замыкания.
Рисунок 2.4 – Упрощенная векторная диаграмма приведенного трансформатора
5.4. Величина отрезка ОС при таком построении равна напряжению U′2н, а угол АОД равен φ1. Действительное напряжение на нагрузке равно
5.5. Сравнить значения напряжений U2н, полученных из расчета полной схемы замещения и из построения упрощенной векторной диаграммы. 6. Построение упрощенных ВД для различных по характеру нагрузок
Повторить описанные выше построения ВД для других углов нагрузки из трех (
Рисунок 2.5 - Упрощенная векторная диаграмма при различных значениях угла φ2
Порядок построения: - из точки «О», как из центра проводится дуга окружности радиусом, равным в принятом масштабе величине напряженияU1; - под угломφ2проводится направление вектора вторичного напряжения -U′2 (φ2>0 - при активно-индуктивной нагрузке, φ2=0 - при чисто активной нагрузке, φ2<0 - при активно-ёмкостной нагрузке); - во всех случаях треугольник к.з. располагается таким образом, чтобы вершина А была на дугеU1, вершина С – на направлении вектора Точки C, C1 и C2 определяют величину U′2 при соответствующемφ2.
Если треугольник АВС поместить в положение ОВ′С′, то дуга, проведенная из вершины С′ радиусомU1, пройдет через точки C, C1 и C2 и является, таким образом геометрическим местом конца вектора Из рисунка 2.5 хорошо видно, что при активно-индуктивной нагрузке и чисто активной нагрузкеU′2<U1. При активно-ёмкостной нагрузке вторичное напряжение U′2может стать больше первичногоU1. 7. Построение зависимости ΔU=f(β) (рисунок 2.6).
7.1 Проверить величину ΔU2% по соотношению ΔU2% =β Uк% cos (φ2 - φк) (2.30) для указанных выше значений φ2, принимая коэффициент нагрузки β=1.
Рисунок 2.6 - Зависимости ΔU2 от коэффициента нагрузки β при различных φ2
8. Для ударного тока короткого замыкания
рассчитать амплитудное значение установившегося тока короткого замыкания
и ударный коэффициент Таблица 2.1 - Варианты задания
Примечания: 1. Номер варианта соответствует номеру в классном журнале. 2. В каждой строчке три варианта, каждому варианту соответствует определенный угол, например:
Поиск по сайту: |
 ;
;
 .
.
 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7) (2.8)
(2.8) ; (2.9)
; (2.9)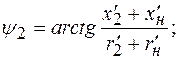 (2.10)
(2.10) ; (2.11)
; (2.11) ; (2.12)
; (2.12) (2.13)
(2.13) (2.14)
(2.14)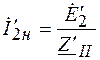 ; (2.15)
; (2.15) ; (2.16)
; (2.16) (2.17)
(2.17) (2.18)
(2.18) .
. откладываются векторы
откладываются векторы  и
и  .
. опережает вектор
опережает вектор  (2.19)
(2.19) , (2.20)
, (2.20) (2.21)
(2.21) . (2.22)
. (2.22) определяется геометрической суммой
определяется геометрической суммой . (2.23)
. (2.23) перпендикулярно току
перпендикулярно току  и в сторону отставания от него откладывается вектор -
и в сторону отставания от него откладывается вектор -  , а из конца этого вектора параллельно току
, а из конца этого вектора параллельно току  . В результате получается вектор вторичного напряжения
. В результате получается вектор вторичного напряжения  и его фазовый сдвиг φ2 относительно тока
и его фазовый сдвиг φ2 относительно тока 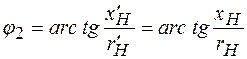 . (2.24)
. (2.24)
 получают в результате графического решения уравнения равновесия токов
получают в результате графического решения уравнения равновесия токов . (2.25)
. (2.25) . Соединив начало координат с концом вектора -
. Соединив начало координат с концом вектора -  .
. производится в соответствии с уравнением равновесия ЭДС
производится в соответствии с уравнением равновесия ЭДС . (2.26)
. (2.26) и
и  необходимо ориентировать перпендикулярно и параллельно вектору тока I1, как показано на рисунке 2.2.
необходимо ориентировать перпендикулярно и параллельно вектору тока I1, как показано на рисунке 2.2. и током
и током  .
. . (2.27)
. (2.27)
 .
. .
. Треугольник АВС располагается на линии -
Треугольник АВС располагается на линии -  , при этом вектор падения напряжения
, при этом вектор падения напряжения  должен опережать вектор
должен опережать вектор  . (2.28)
. (2.28) ) как показано на рисунок 2.5. Оценить изменение напряжения U2н по соотношению
) как показано на рисунок 2.5. Оценить изменение напряжения U2н по соотношению . (2.29)
. (2.29)
 , а катет ВС совпадал по направлению с вектором
, а катет ВС совпадал по направлению с вектором  .
.
 (2.31)
(2.31) (2.32)
(2.32) . (2.33)
. (2.33) .
.