 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Закон сохранения энергии в релятивистском случае
Maple Differential operator, The operator del used in vector analysis and defined as
where i, j, k are unit vectors in the direction of the x-, y- , and z-axes, respectively, and
Векторные поля
C:\Documents and Settings\Alex\Desktop\Лекции 2009\11 лекция 24 11 2009\fieldplot3d 1.mw
C:\Documents and Settings\Alex\Desktop\Лекции 2009\11 лекция 24 11 2009\fieldplot3d 2.mw
Градиент функции есть вектор, направленный в сторону возрастания U, его длина равна частной производной.
Примеры:
C:\Documents and Settings\Alex\Desktop\Лекции 2009\11 лекция 24 11 2009\Grad R.mw
C:\Documents and Settings\Alex\Desktop\Лекции 2009\11 лекция 24 11 2009\Div R.mw
C:\Documents and Settings\Alex\Desktop\Лекции 2009\11 лекция 24 11 2009\Rot R.mw
Законы сохранения
Механическая задача считается решенной, если известно положение движущейся частицы в любой момент времени. Интегрируем.
Закон сохранения импульса
Импульс изолированной системы не изменяется при любых процессах происходящих внутри системы. Закон сохранения импульса для отдельных компонент: В релятивистском случае: так как не существует центра масс, то нельзя интерпретировать движение системы как равномерное и прямолинейное движение центра масс. Т.е. не существует системы отсчета центра масс, в котором импульс равен 0.
Закон сохранения момента импульса Момент импульса Момент силы Продифференцируем момент импульса по времени:
Для изолированной системы:
В инерциальной системе отсчета момент импульса изолированной системы остается постоянным при любых процессах, происходящих внутри системы. У незамкнутых систем может сохраняться не сам момент импульса, а его проекция на некоторую неподвижную ось. Пусть z компонента момента сил равна нулю.
Например, если система движется в вертикальном однородном поле силы тяжести
Закон сохранения энергии в нерелятивистском случае
Пусть m0 движется под действием F.
Умножая (3) на v, получаем:
но Проинтегрируем:
То есть сумма кинетической и потенциальной энергий при движении остается постоянной.
Пример: Одномерное движение.
Закон сохранения энергии в релятивистском случае
Рассуждения относительно работы сил, потенциальности сил и потенциальной энергии справедливы и в случае скоростей, близких к скорости света. Воспользуемся релятивистским уравнением движения.
Дифференцируем левую часть:
То есть, вместо кинетической энергии в результате совершения работы изменяется величина
Если есть поле потенциальных сил U, то
или
То есть, полная энергия равна кинетической энергии и энергии покоя.
Поиск по сайту: |

 ,
, 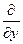 , and
, and  are the respective partial derivatives of the given function of x, y and z. See also gradient, divergence, curl, Laplace operator.
are the respective partial derivatives of the given function of x, y and z. See also gradient, divergence, curl, Laplace operator.

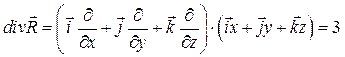
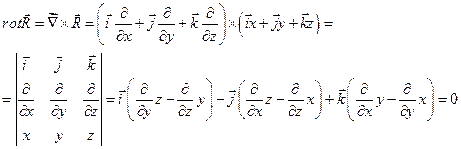


 , тогда
, тогда  .
. .
. .
. ;
;  -уравнение моментов
-уравнение моментов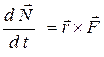 ,
,  ,
,
 , тогда
, тогда  .
.
 (3)
(3)
 или
или 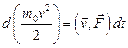 .
.
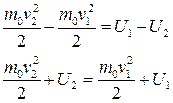






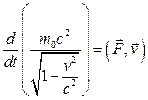



 - полная энергия движущегося тела.
- полная энергия движущегося тела. - Закон сохранения энергии в релятивистском случае.
- Закон сохранения энергии в релятивистском случае. , то есть энергия покоя. Если тело покоится, то его энергия не равна 0. То есть, тело обладает энергией, обусловленной наличием массы.
, то есть энергия покоя. Если тело покоится, то его энергия не равна 0. То есть, тело обладает энергией, обусловленной наличием массы. - масса растет со скоростью. Можно предполагать связь массы и кинетической энергии.
- масса растет со скоростью. Можно предполагать связь массы и кинетической энергии.

 - приращение энергии пропорционально ее релятивистской массы.
- приращение энергии пропорционально ее релятивистской массы.