 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теорема 1. У параллелепипеда противолежащие грани параллельны, и равны.
ТЕМА 10.3. ПАРАЛЛЕЛИПИПЕД И ЕГО СВОЙСТВА. Определение параллелепипеда. Свойства параллелепипеда с доказательствами. Куб. Параллелепи́пед - призма, основанием которой служит параллелограмм. Типы параллелепипеда Различается несколько типов параллелепипедов:
Основные элементы Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро - смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями. Свойства
Основные формулы Прямой параллелепипед Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания Объём V=Sо*h ] Прямоугольный параллелепипед Площадь боковой поверхности Sб=2c(a+b), где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда Площадь полной поверхности Sп=2(ab+bc+ac) Объём V=abc, где a, b, c - измерения прямоугольного параллелепипеда. Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани — параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
Теорема 1. У параллелепипеда противолежащие грани параллельны, и равны.
Доказательство: Рассмотрим какие-нибудь две противолежащие грани параллелепипеда, например Из того, что грани параллелепипеда - параллелограммы, следует, что отрезки
Аналогично доказывается параллельность и равенство любых других противолежащих граней параллелепипеда. Теорема доказана.
Поиск по сайту: |

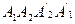 и
и  (рис. 13). Так как все грани параллелепипеда — параллелограммы, то прямая
(рис. 13). Так как все грани параллелепипеда — параллелограммы, то прямая  параллельна прямой
параллельна прямой  , а прямая
, а прямая  параллельна прямой
параллельна прямой 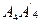 . Отсюда следует, что плоскости рассматриваемых граней параллельны.
. Отсюда следует, что плоскости рассматриваемых граней параллельны. ,
,  ,
,  и
и 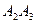 - параллельны и равны. Отсюда заключаем, что грань
- параллельны и равны. Отсюда заключаем, что грань 