|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Енергія електростатичного поля
ПРОВІДНИКИ В ЕЛЕКТРОСТАТИЧНОМУ ПОЛІ Розподіл заряду в провіднику. Зв'язок між напруженістю поля в поверхні провідника й поверхневою густиною заряду
Отже, поверхня провідника при рівновазі зарядів є еквіпотенціальною. При рівновазі зарядів ні в якому місці усередині провідника не може бути надлишкових зарядів – усі вони розподілені по поверхні провідника з деякою густиною σ.
Так як усередині провідника зарядів немає, то потік
тобто вектор електричного зсуву дорівнює поверхневої густині вільних зарядів провідника або
2. Електроємність провідників. Конденсатори ВІДОКРЕМЛЕНИМ називається провідник, віддалений від інших провідників, тіл, зарядів. Потенціал такого провідника прямо пропорційний заряду на ньому
З досвіду випливає, що різні провідники, будучи однаково зарядженими Q1 = Q2здобувають різні потенціали φ1≠ φ2через різну форму, розміри й навколишнього середовища біля провідника (ε). Тому для відокремленого провідника слушна формула
де
Ємність відокремленого провідника дорівнює відношенню заряду q, надавання якого провіднику змінює його потенціал на 1 Вольт.
У системі SI ємність виміряється у Фарадах
Ємність кулі
Розрахуємо ємність плоского конденсатора із площею пластин S, поверхневою густиною заряду σ, діелектричною проникністю ε діелектрика між пластинами, відстанню між пластинами d. Напруженість поля рівна
Використовуючи зв'язок Δφ і Е, знаходимо
ємність плоского конденсатора. Для циліндричного конденсатора:
Для сферичного конденсатора
Так як при деяких значеннях напруги в діелектрику наступає пробій (електричний розряд через шар діелектрика), то для конденсаторів існує пробивна напруга. Пробивна напруга залежить від форми обкладок, властивостей діелектрика і його товщини.
а) паралельне з’єднання
б)послідовне з’єднання
За законом збереження заряду
Енергія електростатичного поля
Електростатичне поле є потенційним. Сили, що діють між зарядами – консервативні сили. Система нерухомих точкових зарядів повинна мати потенційну енергію. Знайдемо потенційну енергію двох нерухомих точкових зарядів q1і q2, що перебувають на відстані r друг від друга Потенційна енергія заряду q2 у поле, створюваному
Аналогічно, потенційна енергія заряду q1 у поле, створюваному зарядом q2, рівна
Видне, що W1 = W2, тоді позначивши потенційну енергію системи зарядів q1 і q2 через W, можна записати
де φi - потенціал, створюваний у тій точці, де перебуває заряд qi, усіма зарядами, крім i-го.
2.Енергія зарядженого відокремленого провідника. Енергію електричного поля зарядженого відокремленого провідника можна визначити, розглянувши сумарну роботу, виконувану по переміщенню невеликих порцій заряду dq з нескінченності на даний провідник. Якщо провідник має заряд q, ємністю С и потенціалом φ, то для того щоб перенести заряд dq з нескінченності на провідник необхідно затратити роботу
Щоб зарядити провідник від нульового потенціалу до потенціалу φ необхідно зробити роботу
Потенційна енергія дорівнює роботі, яку необхідно зробити, щоб зарядити провідник
3. Енергія зарядженого конденсатора. Виразимо енергію конденсатора через величини, що характеризують конденсатор
так як усередині конденсатора поле однорідне, те можна ввести об'ємну густина енергії (об'ємна густина – енергія одиниці об'єму)
Поиск по сайту: |
 Вільні заряди в провіднику здатні переміщатися під дією як завгодно малої сили. Тому для рівноваги зарядів у провіднику повинні виконуватися наступні умови: 1. Напруженість поля усередині провідника повинна дорівнювати нулю
Вільні заряди в провіднику здатні переміщатися під дією як завгодно малої сили. Тому для рівноваги зарядів у провіднику повинні виконуватися наступні умови: 1. Напруженість поля усередині провідника повинна дорівнювати нулю  , тому що
, тому що  т.е. тобто потенціал усередині провідника повинен бути постійним.
т.е. тобто потенціал усередині провідника повинен бути постійним.
 Розглянемо замкнену поверхню у формі циліндра твірні поверхні якого перпендикулярні провіднику. На поверхні провідника розташовані вільні заряди з поверхневою густиноюσ.
Розглянемо замкнену поверхню у формі циліндра твірні поверхні якого перпендикулярні провіднику. На поверхні провідника розташовані вільні заряди з поверхневою густиноюσ. через поверхню циліндра усередині провідника дорівнює нулю. Потік через верхню частину циліндра поза провідником по теоремі Гауса рівний
через поверхню циліндра усередині провідника дорівнює нулю. Потік через верхню частину циліндра поза провідником по теоремі Гауса рівний


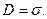

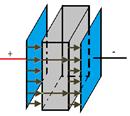 При внесенні незарядженого провідника в зовнішнє електростатичне поле вільні заряди почнуть переміщатися: позитивні - по полю, негативні – проти поля. Тоді з однієї сторони провідника будуть накопичуватися позитивні, а з іншого негативні заряди. Ці заряди називаються ІНДУКОВАНИМИ. Процес перерозподілу зарядів буде відбуватися доти, поки напруженість усередині провідника не стане рівною нулю, а лінії напруженості поза провідником перпендикулярні його поверхні. Індуковані заряди з'являються на провіднику внаслідок зсуву, тобто є поверхневою густиною зміщених зарядів і тому що
При внесенні незарядженого провідника в зовнішнє електростатичне поле вільні заряди почнуть переміщатися: позитивні - по полю, негативні – проти поля. Тоді з однієї сторони провідника будуть накопичуватися позитивні, а з іншого негативні заряди. Ці заряди називаються ІНДУКОВАНИМИ. Процес перерозподілу зарядів буде відбуватися доти, поки напруженість усередині провідника не стане рівною нулю, а лінії напруженості поза провідником перпендикулярні його поверхні. Індуковані заряди з'являються на провіднику внаслідок зсуву, тобто є поверхневою густиною зміщених зарядів і тому що  то тому
то тому 
 ,
, - ємність відокремленого провідника.
- ємність відокремленого провідника.

 між обкладками.
між обкладками.

 .
.

 -
-


 За законом збереження заряду
За законом збереження заряду










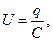






 зарядом q1, рівна
зарядом q1, рівна