 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приклади розв'язання задач
Рішення. Проведемо прямі
Задача (2). У тригранного кута (abc)двогранний кут при ребрі спрямої, двогранний кут при ребрі b дорівнює
Рішення. Опустимо з довільної точки А ребра а перпендикуляр AB на ребро bі перпендикуляр АС на ребро с (рис. 2). По теоремі про три перпендикуляри CB— перпендикуляр до ребра b.
Задача(3). У наклонній призмі проведен перетин, перпендикулярний боковим ребрам, і такий що перетинає всі бокові ребра. Знайдіть бокову поверхню призми, якщо периметр перетину дорівнює р, а бокові ребра рівні l.
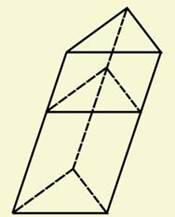
Рішення. Площина проведеного перетину розбиває призму на дві частини (рис. 4). Підвергнемо одну з них паралельному переносу, що з'єднує осови призми. При цьому одержимо пряму призму, у якій основою служить перетин вихідної призми, а бокові ребра дорівнюють l. Ця призма має ту ж боову поверхню, що й вихідна. Таким чином, бокова поверхня вихідної призми дорівнюєpl. Задача(4). Бокове ребро піраміди розділене на чотири рівні частини й через точки ділення проведені площини, паралельні основі. Площа основи дорівнює 400
3адача(5). Доведіть, що бокова поверхня правильної усіченої піраміди дорівнює добутку півсуми периметрів основ на апофему.
Задача (6). Знайдіть двогранні кути правильного тетраедра.
Рішення. Проведемо з вершини S тетраедра висоти SA, SB, SC його граней, що сходяться в цій вершині, і висоту SO тетраедра (рис. 4). Якщо ребро тетраедра позначити через а, то висоти граней будуть рівні Очевидно, двогранні кути при інших ребрах тетраедра такі ж по величині.
Задача (7). Осьовий переріз циліндра — квадрат, площа якого Q. Знайдіть площу основи циліндра.
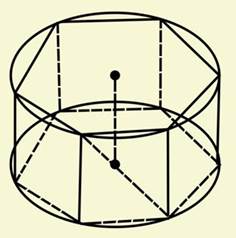
Задача (8). У циліндр вписана правильна шестикутна призма. Знайдіть кут між діагоналлю її бокової грані й віссю циліндра, якщо радіус основи дорівнює висоті циліндра.
Рішення. Бокові грані призми — квадрати, так як сторона правильного шестикутника, вписаного в окружність, дорівнює радіусу (рис. 5). Ребра призми паралельні осі циліндра, тому кут між діагоналлю грані й віссю циліндра дорівнює куту між діагоналлю й боковим ребром. А цей кут дорівнює 45°, так як грані — квадрати.
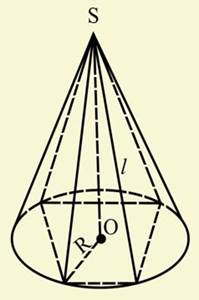
Задача (9). Конус перерізан площиною, що паралельна основі, на відстаніd від вершини. Знайдіть площу перерізу, якщо радіус основи конуса R, а висота H.
Задача (10). У піраміди всі бокові ребра рівні. Доведіть, що вона є вписаною в деякий конус.
Рішення. Опустимо перпендикуляр SO з вершини піраміди на площину основи (рис. 6) і позначимо довжину бокових ребер піраміди через l. Вершини основи віддалені від точки O на одну у ту ж саму відстань
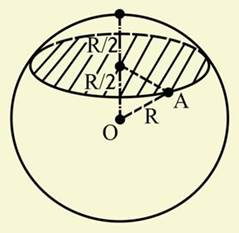
Задача (11). Через середину радіуса кулі проведена перпендикулярна йому площина. Як відноситься площа отриманого перерізу до площі великого кола?
Рішення. Якщо радіус кулі R (рис. 7), то радіус кола в перерізі буде
Задача (12). Доведіть, що центр кулі, описаної біля правильної піраміди, лежить на її осі.
Рішення. Опустимо перпендикуляр ОА із центра кулі О на площину основи піраміди (рис. 10). Нехай X — довільна вершина основи піраміди. По теоремі Піфагора
Задача (13). Куля радіуса R торкається всіх сторін правильного трикутника зі стороною а. Знайдіть відстань від центра кулі до площини трикутника.
Рішення. Нехай A, B, C — точка дотику кулі зі сторонами трикутника (рис. 8). Опустимо із центра О кулі перпендикуляр
Задача (14). Дві рівних кулі радіуса R розташовані так, що центр однієї лежить на поверхні іншої. Знайдіть довжину лінії, по якій перетинаються їхні поверхні.
Рішення. Проведемо переріз через центри куль (рис. 9). Лінія, про яку йде мова в задачі, є окружність (теорема 20.6). Її радіус дорівнює висоті рівностороннього трикутника
Задача (15). Якщо кожне ребро куба збільшити на 2 см, то його об'єм збільшиться на 98 Рішення. Позначимо ребро куба через x, тоді
Задача (16). У прямому паралелепіпеді сторони основиви а й b утворять кут
Рішення. Позначимо висоту через х (рис. 10). Тоді
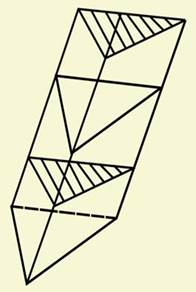
Задача (17). У похилій призмі проведен переріз, перпендикулярний боковим ребрам і перетинаючий всі бокові ребра. Знайдіть об'єм призми, якщо площа перерізу Q, а бокові ребра рівні l.
Рішення. Площина проведеного перерізу розбиває призму на дві частини (рис. 10). Піддамо одну з них паралельному переносу, що сполучає основи призми. При цьому одержимо пряму призму, у якій основою служить переріз вихідної призми, а висота дорівнює l. Ця призма має той же об'єм. Таким чином, об'єм вихідної призми дорівнює Ql.
Задача (18). Знайдіть об'єм усіченої піраміди із площами основ
Рішення. Доповнимо дану усічену піраміду до повної (рис. 11). Нехай х — її висота. Об'єм усіченої піраміди дорівнює різниці об'ємів двох повних пірамід: однієї із площею основи
Задача (19). Через середину висоти піраміди проведена площина, паралельна основі. У якому відношенні вона ділить об'єм піраміди?
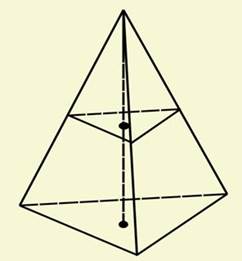
Рішення. Як ми знаємо, проведена площина відтинає подібну піраміду (рис. 12). Коефіцієнт подоби дорівнює відношенню висот, тобто
Задача (20). Знайдіть об'єм усіченого конуса, у якого радіуси основ
Рішення. Доповнимо даний усічений конус до повного (рис. 490). Нехай x — його висота. Об'єм усіченого конуса дорівнює різниці об'ємів двох повних конусів: одного з радіусом основи
Поиск по сайту: |
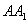 й
й  на ребро кута. Знайдіть довжину відрізка
на ребро кута. Знайдіть довжину відрізка 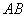 , якщо
, якщо  ,
, 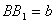 ,
,  і двогранний кут дорівнює
і двогранний кут дорівнює 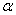 (рис. 1).
(рис. 1).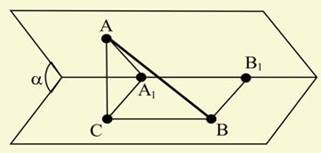
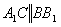 й
й 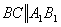 . Чотирикутник
. Чотирикутник 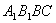 — паралелограм, значить
— паралелограм, значить 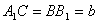 . Пряма
. Пряма 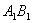 перпендикулярна площині трикутника
перпендикулярна площині трикутника 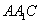 , тому що вона перпендикулярна двом прямим у цій площині
, тому що вона перпендикулярна двом прямим у цій площині  . Отже, паралельна їй пряма
. Отже, паралельна їй пряма 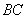 теж перпендикулярна цієї площині. Виходить, трикутник
теж перпендикулярна цієї площині. Виходить, трикутник  — прямокутний із прямим кутом C. По теоремі косинусів
— прямокутний із прямим кутом C. По теоремі косинусів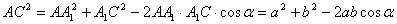 .
.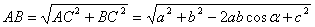 .
.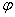 , а плоский кут (bc)дорівнює
, а плоский кут (bc)дорівнює 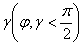 . Знайдіть два інших плоских кути:
. Знайдіть два інших плоских кути:  ,
, 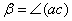 .
.

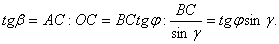
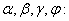
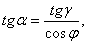
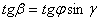 —
—
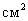 . Знайдіть площі перетинів.
. Знайдіть площі перетинів. 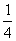 ,
,  і
і 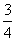 . Площі подібних фігур відносяться як квадрати лінійних розмірів. Тому відносини площ перетинів до площі основи піраміди є
. Площі подібних фігур відносяться як квадрати лінійних розмірів. Тому відносини площ перетинів до площі основи піраміди є 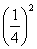 ,
, 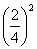 і
і  . Отже площі перетинів рівні
. Отже площі перетинів рівні 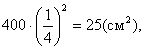
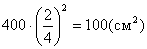 ,
, 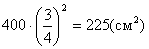 .
.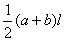 . Площа всіх граней, тобто бокова поверхня, дорівнює —
. Площа всіх граней, тобто бокова поверхня, дорівнює —  , де n — число вершин у основі піраміди, an і bn — периметри основ піраміди.
, де n — число вершин у основі піраміди, an і bn — периметри основ піраміди.
 . З рівності висот SA, SB, SC слідує рівність відрізків OA, OB, OC. А вони перпендикулярні сторонам трикутника в основі тетраедра (по теоремі про три перпендикуляри). Звідси слідує, що точка О є центром окружності, що вписана в основу тетраедра. Отже, відрізки OA, OB, і OC рівні
. З рівності висот SA, SB, SC слідує рівність відрізків OA, OB, OC. А вони перпендикулярні сторонам трикутника в основі тетраедра (по теоремі про три перпендикуляри). Звідси слідує, що точка О є центром окружності, що вписана в основу тетраедра. Отже, відрізки OA, OB, і OC рівні  . Позначимо через
. Позначимо через 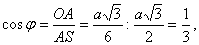
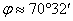 .
. . Вона дорівнює діаметру основи. Тому площа основи дорівнює
. Вона дорівнює діаметру основи. Тому площа основи дорівнює 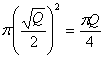 .
.
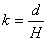 . Тому радіус кола в перерізі
. Тому радіус кола в перерізі 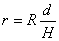 Отже, площа перерізу
Отже, площа перерізу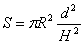 .
.
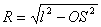 .
.
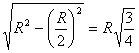 . Відношення площі цього кола до площі великого кола дорівнює
. Відношення площі цього кола до площі великого кола дорівнює 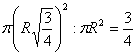 .
.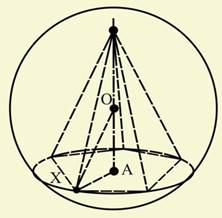

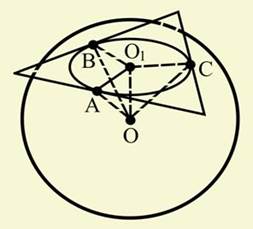
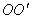 на площину трикутника. ВідрізкиOA, OB і OC перпендикулярні сторонам. По теоремі про три перпендикуляри відрізки
на площину трикутника. ВідрізкиOA, OB і OC перпендикулярні сторонам. По теоремі про три перпендикуляри відрізки 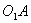 ,
, 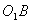 і
і 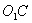 теж перпендикулярні відповідним сторонам трикутника.
теж перпендикулярні відповідним сторонам трикутника.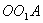 ,
, 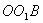 ,
, 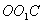 (у них катет загальний, а гіпотенузи дорівнюють радіусу) слідує рівність сторін:
(у них катет загальний, а гіпотенузи дорівнюють радіусу) слідує рівність сторін: 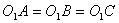 . Отже,
. Отже,  — центр окружності, вписаної в трикутник. Радіус цієї окружності, як ми знаємо, дорівнює
— центр окружності, вписаної в трикутник. Радіус цієї окружності, як ми знаємо, дорівнює  .
.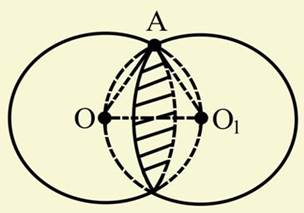
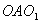 зі сторонами, рівними
зі сторонами, рівними 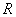 . Висота дорівнює
. Висота дорівнює  . Отже, довжина лінії дорівнює
. Отже, довжина лінії дорівнює  .
. . Чому дорівнює ребро куба?
. Чому дорівнює ребро куба?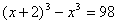 , тобто
, тобто 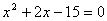 . Рівняння має два корені: x=3, x=-5. Геометричний зміст має тільки не від'ємний корінь. Отже, ребро куба дорівнює 3 см.
. Рівняння має два корені: x=3, x=-5. Геометричний зміст має тільки не від'ємний корінь. Отже, ребро куба дорівнює 3 см.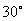 . Бокова поверхня дорівнює S. Знайдіть його об'єм.
. Бокова поверхня дорівнює S. Знайдіть його об'єм.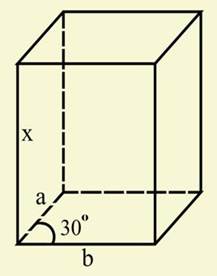


 . Об'єм дорівнює
. Об'єм дорівнює 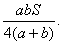
 і
і 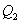 (
( 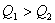 ) і висотою h.
) і висотою h.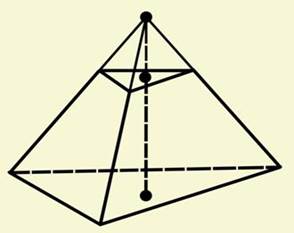
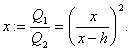
 Об'єм усіченої піраміди дорівнює:
Об'єм усіченої піраміди дорівнює:
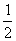 .
.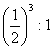 . Отже, площина ділить нашу піраміду на частини, об'єми яких відносяться як
. Отже, площина ділить нашу піраміду на частини, об'єми яких відносяться як 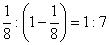 .
.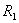 і
і 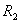 (
( 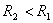 ), а висота h.
), а висота h.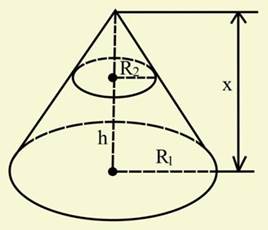
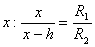 ,
, 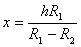 .
.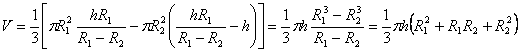 .
.