 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расстояние от точки до плоскости
Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Расстоянием Пусть
Рис. 23 На (рис.23)
Расстояние между параллельными плоскостями. Если плоскости параллельны, то все точки любой из них находятся на одинаковом расстоянии от второй плоскости. Поэтому под расстоянием
тогда
Рис. 24
Угол между плоскостями Две пересекающиеся плоскости образуют четыре двухгранных угла. Любой из этих углов называют углом между данными плоскостями. Пусть плоскости
плоскостей:
В частности, плоскости перпендикулярны тогда и только тогда, когда
Рис. 25 ПРЯМЫЕ В ПРОСТРАНСТВЕ Уравнения прямой. Уравнение прямой, проходящей через данную точку параллельно данному вектору Так как через каждую точку пространства в данном направлении проходит единственная прямая, то так же, как и в случае плоскости, ее векторное параметрическое уравнение имеет вид:
где Пусть в аффинной системе координат
Рис. 26 Исключая из параметрических уравнений (17’) параметр t, приходим к каноническим уравнениям прямой. Если направляющий вектор прямой не имеет нулевых координат, то эти уравнения записываются так:
Если одна из координат вектора
Заметим, что при
Прямая (20) параллельна оси
Поиск по сайту: |
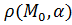 от точки
от точки  до плоскости
до плоскости  называется длина перпендикуляра, опущенного из этой точки на плоскость.
называется длина перпендикуляра, опущенного из этой точки на плоскость. ,
,  , тогда
, тогда

 – перпендикуляр, опущенный из
– перпендикуляр, опущенный из  между параллельными плоскостями будем понимать расстояние от любой точки одной из них до другой плоскости. Пусть параллельные плоскости
между параллельными плоскостями будем понимать расстояние от любой точки одной из них до другой плоскости. Пусть параллельные плоскости  и
и  заданы соответственно уравнениями:
заданы соответственно уравнениями:




 . Поэтому косинус угла
. Поэтому косинус угла  вычисляется по формуле
вычисляется по формуле


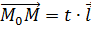 (17)
(17) – направляющий вектор.
– направляющий вектор.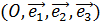 :
:  . Векторное уравнение (17) эквивалентно трем скалярным:
. Векторное уравнение (17) эквивалентно трем скалярным: (17’)
(17’)

 , например
, например  равна нулю, то эти уравнения имеют такой вид:
равна нулю, то эти уравнения имеют такой вид:
 , прямая параллельна плоскости
, прямая параллельна плоскости  . Наконец, если две координаты вектора
. Наконец, если две координаты вектора  равны нулю, то прямая определяется уравнениями:
равны нулю, то прямая определяется уравнениями: ,
,  (20)
(20) .
.