 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Випадкова похибка середнього арифметичного ⇐ ПредыдущаяСтр 2 из 2
Як уже зазначалося, усереднення результатів повторних вимірювань дозволяє зменшити випадкову похибку. Зв'язок середнього квадратичного відхилення випадкової похибки середнього арифметичного
де Таким чином, випадкова похибка середнього арифметичного в Розрахунок довірчих границь випадкової похибки середнього арифметичного проводиться за вказаними вище для випадкової похибки результату одиничного вимірювання формулами з відповідною заміною середнього квадратичного відхилення. Причому, дані формули для середнього арифметичного справедливі навіть в тому випадку, коли результати одиничних вимірювань не розподілені за нормальним законом. Це обумовлено тим, що відповідно до центральної граничної теореми теорії ймовірності незалежно від розподілу результатів одиничних вимірювань середнє арифметичне буде розподілене приблизно за нормальним законом. Розподіл середнього арифметичного тим ближчий до нормального, чим більша кількість результатів використовується під час розрахунку середнього значення. Отже, збільшення числа повторних вимірювань в умовах збіжності та наступна їхня спільна математична обробка (усереднення) дозволяє зменшити випадкову похибку до як завгодно малого значення. Однак, насправді, зменшувати випадкову похибку є сенс лише в тому випадку, якщо вона в сумі з систематичною перевищує допустиму величину. По-друге, навіть коли сумарна похибка перевищує прийнятне значення або необхідно досягти максимально можливої точності, немає сенсу зменшувати випадкову похибку, якщо вона неістотна в порівнянні з систематичною. Неістотною вважається випадкова похибка, яка в три чи більше разів менша від систематичної. В такому разі зменшення випадкової похибки вже не буде впливати на точність результату вимірювання, оскільки домінувати буде систематична похибка.
Поиск по сайту: |
з середнім квадратичним відхиленням випадкової похибки результату одиничного вимірювання 
дається залежністю
,
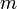-число результатів повторних вимірювань, для яких розраховувалося середнє значення.
раз менша від випадкової похибки результату одиничного вимірювання. Наприклад, якщо випадкову похибку необхідно зменшити в 2 рази, то число результатів повторних вимірювань, за якими буде розраховано середнє значення, необхідно збільшити в 4 рази.