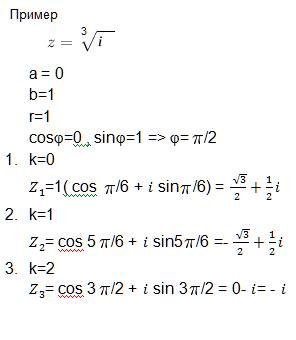|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Действия над комплексными числами
Лекция Комплексные числа. Определение Комплексным числом zназывается выражение
При этом число a называется действительной частьючисла z (a = Re z), а b-мнимой частью(b = Im z). Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным. Определение Числа Определение Два комплексных числа
Определение Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.
Геометрическое изображение комплексного числа. Всякое комплексное число Плоскость на которой изображаются комплексные числа, называются комплексной плоскостью.
OM = (a, b)
При этом величина rназывается модулемкомплексного числа, а угол j-аргументомкомплексного числа.
Аргумент комплексного числа Z ≠ 0 – величина многозначная и определяется с точностью до слагаемого 2
При решение задач чаще всего используют главное значение аргумента. Для комплексного числа z=0 –аргумент не определен.
Тригонометрическая форма комплексного числа.
Из геометрических соображений видно, что
Такая форма записи называется тригонометрической формой записи комплексного числа. Формула Выражение вида Действия над комплексными числами. 1) Сложение и вычитание.
2) Умножение.
3) Деление.
4) Возведение комплексного числа в степень.
где n –целое положительное число.
Это выражение называется формулой Муавра. 5) Извлечение корня из n– ой степени комплексного числа.
Таким образом, корень n– ой степени из комплексного числа имеет n различных значений для k=0,1,...,n-1.
Поиск по сайту: |
 , где a и b– действительные числа,i– мнимая единица, которая определяется соотношением:
, где a и b– действительные числа,i– мнимая единица, которая определяется соотношением:
 и
и 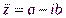 называются комплексно – сопряженными.
называются комплексно – сопряженными. и
и  называются равными, если соответственно равны их действительные и мнимые части:
называются равными, если соответственно равны их действительные и мнимые части:

 можно изобразить точкойM (a, b) и взять a =Re z , а b = Im z комплексного числа.
можно изобразить точкойM (a, b) и взять a =Re z , а b = Im z комплексного числа.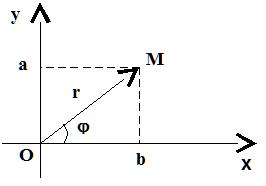 Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При ось Ох будет являться действительной числовой осью, а ось Оу - мнимой осью.
Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При ось Ох будет являться действительной числовой осью, а ось Оу - мнимой осью. Комплексное числотакже можно изобразить на комплексной плоскостив виде радиус-вектора ОМ
Комплексное числотакже можно изобразить на комплексной плоскостив виде радиус-вектора ОМ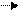 Длина радиус-вектора ОМ называется модулем комплексного числа.
Длина радиус-вектора ОМ называется модулем комплексного числа.



 k,где k целое число.
k,где k целое число.
 главное значение аргумента.
главное значение аргумента.


 . Тогда комплексное число можно представить в виде:
. Тогда комплексное число можно представить в виде:
 называется формулой Эйлера.
называется формулой Эйлера. называется показательной формой записи комплексного числа, где r - модуль комплексного числа, аj-аргументомкомплексного числа
называется показательной формой записи комплексного числа, где r - модуль комплексного числа, аj-аргументомкомплексного числа





 ,
,