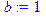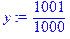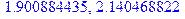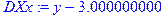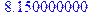|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
по дисциплине «Синергетика»
Отчет по зачетной работе «Моделирование экономического развития» по дисциплине «Синергетика»
Выполнил: студент группы ИН-31 Калиниченко Ю.В. Проверил: преподаватель Шатров А.В.
Задание: составить модель динамики экономики с дополнительными эффективностями. Данная модель описывается следующей системой уравнений:
х(t) – валовый продукт в стоимостном выражении, y(t) – темп роста валового продукта, z(t) – платежеспособный спрос (денежные ресурсы потребителей), Начальные условия X(0)=0 Y(0)=0 С помощью пакета Maple исследуем модель Находим решения x* и y*, исследуем положение равновесия: > dx:=x*y-(k+(1/r1))*x; y1:=k+1/r1;
> dy:=a*x*y + e2*x*y^2 - e1*y^2 - yy*y - b*(x-z);
> x1:=(e1(y1)^2+yy*y1-z*b)/(a*y+e2*y^2-b); >
> DXx:=diff(dx,x);
> DYx:=diff(dx,y);
> DXy:=diff(dy,x);
> DYy:=diff(dy,y);
Находим типовые решения x* и y*: > y:=y1;
> x:=x1;
> DXx;
> DYy;
> DXy;
> DYx;
Анализируем систему уравнений, подставляя различные значения коэффициентов: 1) r1 – время существования продукта (живучесть). Возьмем r1->беск и r2->беск. В этом случае спрос будет только расти и продукт увеличиваться. Равновесие с точки зрения спроса не существует => данный вариант не рассматривается. 2) r1->беск, r2(1..10), k ~ 1, α(темпы роста) ~ 0.1, ε2 – организационные мероприятия. ε2~ ε1 (0..1), β~1 Рассмотрим данную систему в maple: > x:='x'; y:='y'; k:=1; yy:=1; b:=1; a:=0.05; e1:=1; e2:=1; r1:=1000; r2:=1; dx:=x*y-(k+(1/r1))*x; y1:=k+1/r1;
> dy:=a*x*y + e2*x*y^2 - e1*y^2 - yy*y - b*(x-z);
> x1:=(e1(y1)^2+yy*y1-z*b)/(a*y+e2*y^2-b); >
> DXx:=diff(dx,x);
> DYx:=diff(dx,y);
> DXy:=diff(dy,x);
> DYy:=diff(dy,y);
> y:=y1;
> x:=x1;
> DXx;
> DYy;
> DXy;
> DYx;
> solve(z^2-DYy*z-DYx*DYy=0,z);
λ1>0 и λ2>0 – неустойчивый узел, т.к r1->беск (нет износа товаров). График для данной системы: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1+2)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..15,[[x(0)=1,y(0)=0,z(0)=1]],stepsize=.05, scene=[x(t),y(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
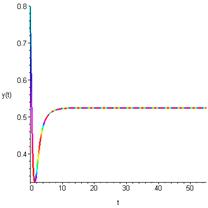
Отдельно рассмотрим графики: График X: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..55,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[t,x(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
График Y: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..55,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[t,y(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
График z: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..55,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[t,z(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
3) Рассмотрим систему уравнений и примем r1 (0..1), r2=(1..10) 4)> x:='x'; 5) y:='y'; 6) k:=1; 7) yy:=1; 8) b:=1; 9) a:=0.05; 10) e1:=1; 11) e2:=1; 12) r1:=0.5; 13) r2:=1; 14) dx:=x*y-(k+(1/r1))*x; 15) y1:=k+1/r1; 16) 17) 18) 19) 20) 21) 22) 23) 24) 25) 26) 27) 28) > dy:=a*x*y + e2*x*y^2 - e1*y^2 - yy*y - b*(x-z); 29) 30) > x1:=(e1(y1)^2+yy*y1-z*b)/(a*y+e2*y^2-b); 31) > 32) 33) > DXx:=diff(dx,x); 34) 35) > DYx:=diff(dx,y); 36) 37) > DXy:=diff(dy,x); 38) 39) > DYy:=diff(dy,y); 40) 41) > y:=y1; 42) 43) > x:=x1; 44) 45) > DXx; 46) 47) > DYy; 48) 49) > DXy; 50) 51) > DYx; 52) 53) > solve(z^2-DYy*z-DYx*DYy=0,z); 54)
λ1<0 и λ2<0 => устойчивый узел Рассмотрим график: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1+2)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..55,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[x(t),y(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
Отдельно рассмотрим графики: x: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1+2)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..5,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[t,x(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
график y: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1+2)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..5,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[t,y(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
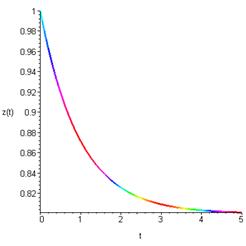
график z: > with(DEtools): > phaseportrait([D(x)(t)=x(t)*y(t)-(1+2)*x(t),D(y)(t)=0.05*x(t)*y(t)+x(t)*y(t)^2-y(t)^2-1*y(t)-x(t)+z(t),D(z)(t)=0.8-z(t)], [x(t),y(t),z(t)],t=0..5,[[x(0)=1,y(0)=0.8,z(0)=1]],stepsize=.05, scene=[t,z(t)],linecolour=sin(t*Pi/2),method=classical[foreuler]);
Вывод: модель динамики экономики с дополнительными эффективностями была проанализирована, были найдены значения коэффициентов, при которых модель становится устойчивой и неустойчивой.
Поиск по сайту: |
 , где
, где показывает уменьшение валового продукта в единицу времени из-за непроизводительных затрат, r1 и k – коэффициенты непроизводительных затрат,
показывает уменьшение валового продукта в единицу времени из-за непроизводительных затрат, r1 и k – коэффициенты непроизводительных затрат,  показывает увеличение темпа работы из-за вовлечения в процесс производства созданного валового продукты и трудового ресурса,
показывает увеличение темпа работы из-за вовлечения в процесс производства созданного валового продукты и трудового ресурса, 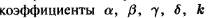 - эффективности соответствующих процессов.
- эффективности соответствующих процессов.