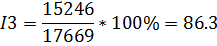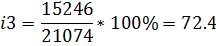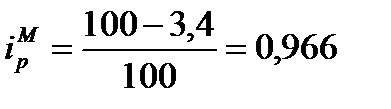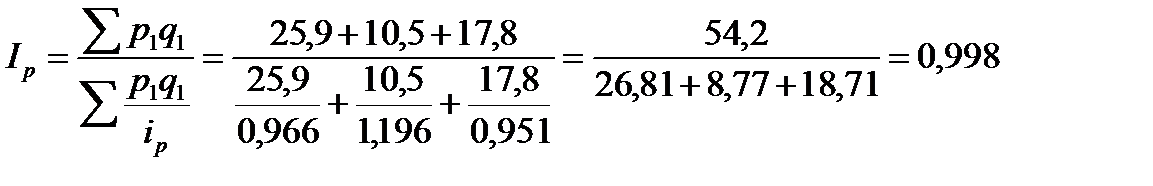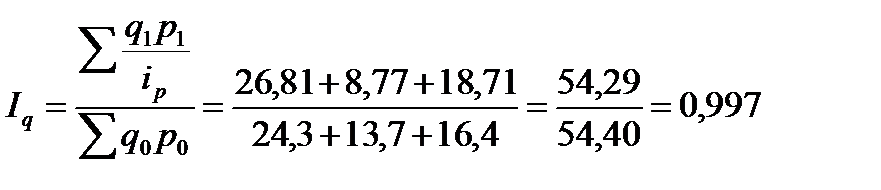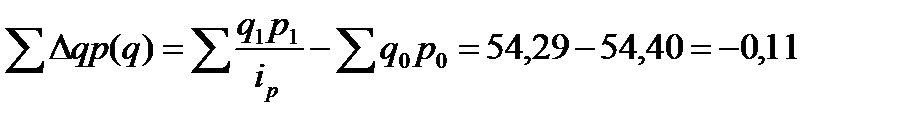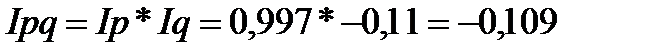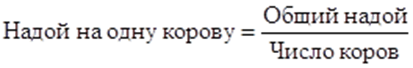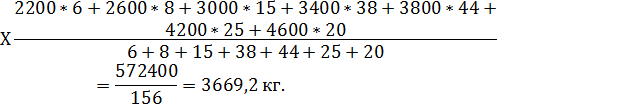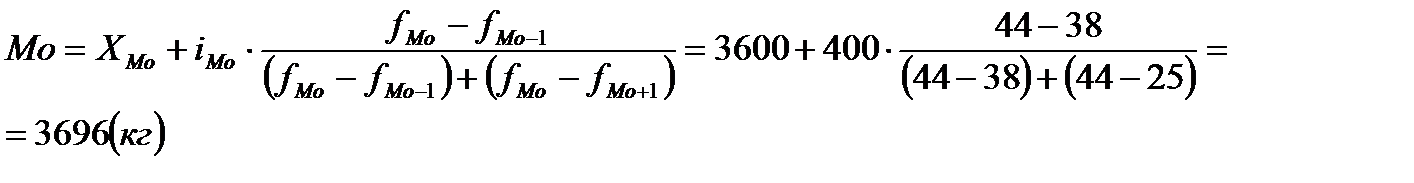|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вопрос №13 «Виды и формы средних величин и методы их расчета» ⇐ ПредыдущаяСтр 2 из 2
Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы. Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой. Используются две категории средних величин: 1. степенные средние: - среднюю арифметическую; - среднюю гармоническую; - среднюю квадратическую; - среднюю геометрическую. 2. структурные средние: - мода; - медиана.
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности. где n - численность совокупности.
В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид:
Где:
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
Где: где n - численность совокупности.
гармоническая взвешенная: Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель. Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической. Простая средняя геометрическая:
взвешенная средняя геометрическая: Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).
- простая средняя квадратическая:
- взвешенная средняя квадратическая:
Выбор средней обусловлен задачами исследования и наличием исходной информации.
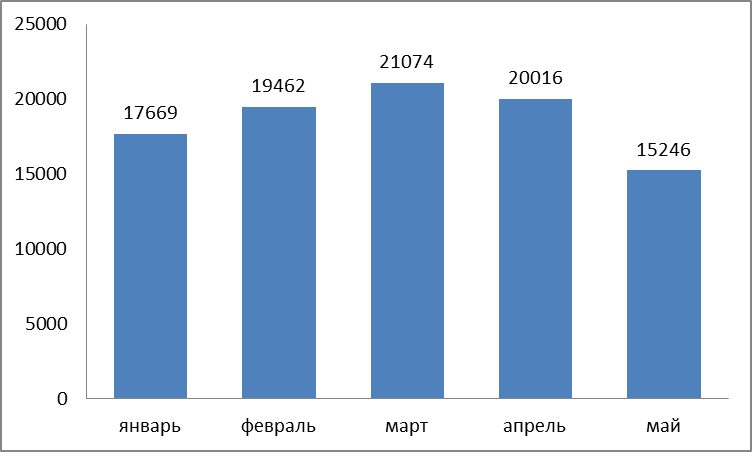
Практическое задание Задача №49 Имеются показатели объема реализации продуктов на рынках города с января по май.
Определите цепным и базисным методом: А) Абсолютный прирост:
Б) Темп роста:
В)Темп прироста:
Г) динамику реализации продукции изобразите столбиковой или линейной диаграммой. Динамик реализации молока:
Задача №60
Определите общие индексы цен, товарооборота. Сделайте краткие экономические выводы. Решение: Исходя из изменения цен в текущем периоде по сравнению с базисным можно найти индивидуальные индексы цен (р1/ р0):
1. Общий индекс цен исчисляется по формуле
Если в данной формуле из числителя вычесть знаменатель, то получается показатель прироста товарооборота в текущем периоде в результате изменения цен: 2. Общий индекс физического объема товарооборота равен:
Прирост суммы товарооборота в текущем периоде в результате изменения физического объема продаж определяется следующим образом:
Поскольку величина объема товарооборота равна произведению количества продажи товаров на цены, то общий индекс физического объема Iq, умноженный на общий индекс цен Iр, дает общий индекс товарооборота Iqр:
Таким образом, из приведенных расчетов видно, что рост цен по ассортименту в целом на 9,98% вызвало уменьшение товарооборота на 0,09 тыс. руб. Падение физического объема товарооборота вызвало снижение товарооборота на 0,11 тыс. руб. В результате совокупного действия этих факторов объем товарооборота в текущем периоде по сравнению с базисным упал на 0,109 тыс. руб.
Задача№ 31
Определить: 1) Среднегодовой надой молока на 1 корову, кг. Таблица 1. Расчет вспомогательных значений для определения характеристик ряда распределения
Размах вариации = 400. Расчет среднего надоя молока на одну корову произведем по формуле средней арифметической взвешенной:
Ответ: средний надой молока на одну корову составляет 3669,2 кг. 2) Моду и медиану среднегодовой продукции, кг. Мода:
Большинство коров дают надой молока в среднем 3696 кг. Медиана:
Половина коров дают надой молока менее 3700 кг, другая половина – более 3700 кг.
Задача №24 Произведите группировку хозяйств по поголовью коров. Образуйте три группы со следующими интервалами: до 1000; 1000-1500; свыше 1500. По каждой группе и в целом по всем хозяйствам вместе подсчитайте: 1. Число хозяйств по группам; 2. Поголовье коров, гол; 3. Площадь с/х угодий, га; 4. Поголовье коров на 100 га с/х угодий, гол; Решение задачи оформите статистической таблицей. Имеются следующие данные:
Решение: Для формирования аналитической группировки строим вспомогательную таблицу. Таблица 1. Разработочная таблица группировки хозяйств
На основе разработочной таблицы формируем аналитическую группировку. Таблица 2. Аналитическая группировка хозяйств по поголовью коров.
На основании аналитической группировки необходимо сделать вывод о прямой связи между показателями, т. к. они все в среднем одновременно растут.
Список литературы 1. Боярский А.Я., Громыко Г.Л. Общая теория статистики. М.: «Московские университеты», 1985. 2. Курс социально-экономической статистики: учебник для вузов/под ред. проф. М.Г. Назарова. М.: Финстатинформ, 2000. 3. Общая теория статистики. Под редакцией Г.С. Кильдишева и др. М.: Статистика, 1980. 4. Общая теория статистика. Под редакцией А.А. Спирина и др. М.: Финансы и статистика, 1996. 5. Ряузов Н.Н. Общая теория статистики. М.: Статистика, 1979.
Поиск по сайту: |
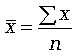
 - средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
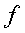 - частота (повторяемость индивидуальных значений признака).
- частота (повторяемость индивидуальных значений признака). - величины, для которых исчисляется средняя;
- величины, для которых исчисляется средняя;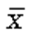 - средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;
- средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;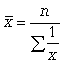
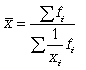

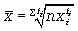
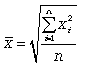
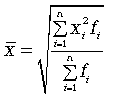
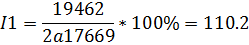
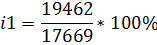
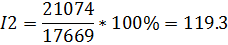
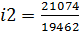 *100%=108.3
*100%=108.3