 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Закон Ома для переменного тока
Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:
Реактивное сопротивление – это сопротивление катушек индуктивности (дросселей) и конденсаторов. Величина реактивного сопротивления уже зависит от частоты тока. Так на постоянном токе реактивное сопротивление конденсатора устремляется к бесконечности, а дросселя наоборот – к нулю (без учета активной составляющей сопротивления провода). С изменением частоты тока электрическое сопротивление конденсатора изменяется, по закону: Xc = 1/2pfC2где Xc – сопротивление, Ом; f – частота, Гц; С – емкость, Ф. Электрическое сопротивление конденсатора переменному току можно измерить. Зная сопротивление и частоту тока, легко по формуле вычислить емкость. Кроме того, если в электрической цепи стоит конденсатор происходит сдвиг фаз напряжения и тока. Причем ток опережает напряжение на величину 90°. Реактивное сопротивление катушки индуктивности с увеличением частоты возрастает: XL = 2pfLгде XL – сопротивление катушки, Ом; f – частота, Гц; L – индуктивность, Гн. Индуктивность дросселя легко вычисляется по известному сопротивлению и заданной частоте тока. При этом фазы напряжения и тока на катушке индуктивности сдвигаются относительно друг друга, и теперь ток отстает от напряжения на 90°. Для измерения реактивного сопротивления емкости и индуктивности потребуется, прежде всего, переменный ток синусоидальной формы. С задачей программного генератора с легкостью может справиться звуковая плата компьютера. Другая проблема – определение величины электрического сопротивления измеряемого элемента. Но оказывается и эту задачу можно решить программным путем, с помощью той же звуковой платы, не прибегая к специальным аналого-цифровым преобразователям 2. Импеданс - это полное сопротивление в цепи переменного тока, т.е. его активная и реактивная составляющие. Обозначают импеданс буквой – Z В общем случае мгновенное значение силы тока i определяется по формуле где j - разность (сдвиг) фаз между колебаниями тока и напряжения, Im – амплитуда силы тока. · В проводнике с активным сопротивлением (резисторе) колебания силы тока по фазе совпадают с колебаниями напряжения, а амплитуда силы тока определяется равенством · В катушке индуктивности колебания силы тока отстают от колебаний напряжения на угол j=p/2. Амплитуда силы тока в катушке равна · На конденсаторе колебания силы тока опережают колебания напряжение на угол j=p/2. Амплитуда силы тока равна: Полное сопротивление цепи равно:
Разность X = (XL - XC) называется реактивным сопротивлением цепи. R называется активным сопротивлением цепи. Для построения зависимости
Затем графики зависимостей
3. Электрический диполь-это совокупность двух равных по величине разноимённых точечных зарядов q, расположенныхна некотором расстоянии l друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля. Электрическими диполями являются полярные молекулы, например молекула воды, совокупность диполей представляют мембраны клеток. Для фиксированных угловых координат (то есть на луче, идущем из центра электрического диполя на бесконечность) напряжённость статического[прим 4] электрического поля диполя или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент,[прим 5] на больших расстояниях r асимптотически приближается к виду r−3, электрический потенциал — к r−2. Таким образом, статическое поле диполя убывает на больших расстояниях быстрее, чем поле простого заряда (но медленнее, чем поле любого более старшего мультиполя). Напряжённость электрического поля и электрический потенциал неподвижного или медленно движущегося диполя (или в целом нейтральной системы зарядов, имеющей ненулевой дипольный момент) с электрическим дипольным моментом на больших расстояниях в главном приближении выражается как: в СГСЭ: в СИ: Достаточно просты выражения (в том же приближении, тождественно совпадающие с формулами, приведенными выше) для продольной (вдоль радус-вектора, проведенного от диполя в данную точку) и поперечной компонент напряженности электрического поля:
Поиск по сайту: |
 U = U0eiωt — напряжение или разность потенциалов ,I — сила тока ,Z = Re−iδ — комплексное сопротивление (импеданс), R = (Ra2 + Rr2)1/2 — полное сопротивление ,Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного), Rа — активное (омическое) сопротивление, не зависящее от частоты,δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.
U = U0eiωt — напряжение или разность потенциалов ,I — сила тока ,Z = Re−iδ — комплексное сопротивление (импеданс), R = (Ra2 + Rr2)1/2 — полное сопротивление ,Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного), Rа — активное (омическое) сопротивление, не зависящее от частоты,δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока. ,
,  где R – (активное) сопротивление резистора.
где R – (активное) сопротивление резистора. . Величину XL =wL = 2pfL называют индуктивным сопротивлением.
. Величину XL =wL = 2pfL называют индуктивным сопротивлением. . Величину
. Величину  называют емкостным сопротивлением.
называют емкостным сопротивлением. 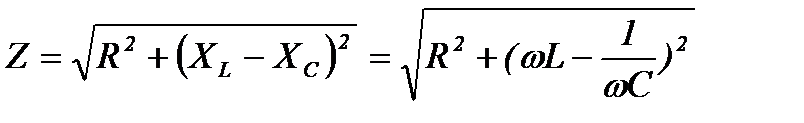 а сдвиг фаз между током и напряжением
а сдвиг фаз между током и напряжением 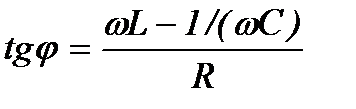
 от частоты w вначале строятся зависимости
от частоты w вначале строятся зависимости 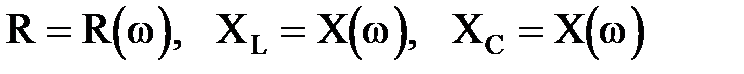 (рис.2,3,4)
(рис.2,3,4)
 представляем на одном рисунке (рис.5). Указанные кривые пересекаются. Точка пересечения этих графиков означает, что при определенном значении частоты источника переменного
представляем на одном рисунке (рис.5). Указанные кривые пересекаются. Точка пересечения этих графиков означает, что при определенном значении частоты источника переменного тока w емкостное сопротивление конденсатора и индуктивное сопротивления катушки индуктивности равны, т. е. XC=XL или
тока w емкостное сопротивление конденсатора и индуктивное сопротивления катушки индуктивности равны, т. е. XC=XL или 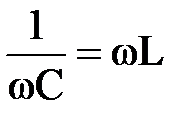 и тогда
и тогда  .
.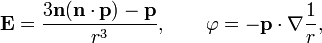
 где — единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение.
где — единичный вектор из центра диполя в направлении точки измерения, а точкой обозначено скалярное произведение. где θ — угол между направлением вектора дипольного момента и радиус-вектором в точку наблюдения (формулы приведены в системе СГС; в СИ аналогичные формулы отличаются только множителем ). Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор, — всегда равна нулю.
где θ — угол между направлением вектора дипольного момента и радиус-вектором в точку наблюдения (формулы приведены в системе СГС; в СИ аналогичные формулы отличаются только множителем ). Третья компонента напряженности электрического поля — ортогональная плоскости, в которой лежат вектор дипольного момента и радиус-вектор, — всегда равна нулю.