 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ
КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ В математике очень широко применяется решение задач с помощью комплексных чисел, но что такое комплексные числа и как они нашли себя в электротехнике? Первоначально математики столкнулись с мнимой единицей i= решили, что корень из отрицательного числа не имеет смысла. И это работало, было легко показать, что при отрицательном корне, решением было ни положительное число, ни отрицательное, ни нуль. Однако в дальнейшем, при решении кубических уравнений отказываться от отрицательного корня уже было невозможно. математики пошли на изучение мнимых чисел, дали возможность им существовать. Затем было обнаружено, что многие громоздкие задачи в математике решаются гораздо проще, если пользоваться мнимыми числами. К.Ф. Гаусс предложил называть мнимые числа комплексными, что впоследствии прижилось. вскоре ученые столкнулись с проблемой при решении задач электротехники. Описание электромагнитных процессов в цепях переменного тока сводится к решению множества интегралов, а решение их становится столь сложным, что взять их не по силу даже опытным математикам. Определение крайне упростилось и стало более элегантно при применении комплексных чисел. Наиболее удобная для проведения расчетов координатная система стала комплексная, так как вектор можно определить четырьмя различными формами записи: · Алгебраическая форма: · Тригонометрическая форма: · Показательная форма: · Полярная форма: Рассмотрим типичную задачу в электротехнике: сложение токов. представим, что фаза у токов отличается. Например,
Рисунок 4. Синусоиды тока с разной фазой
Решение:
по формуле суммы углов:
Воспользуемся методом введения дополнительного угла, чтобы привести уравнение к виду: Так как у нас есть составляющие: По основному тождеству тригонометрии:
Находим
Подставляем в
Как видим, такая, простая на первый взгляд, задача переливается в уравнение, которое заставит посидеть и подумать «как же оно решается.Теперь рассмотрим эту задачу с применением комплексных чисел, мы уже знаем, что такое комплексное число и в состоянии перевести в него уравнение синусоиды тока. Итак:
сложим:
Решение в 2 строки, а результаты те же. Выводы: На этом простейшем примере хорошо видно как комплексные числа упростили решение. Сейчас же ни одна задача в электротехнике не решается без них. Мнимые числа необходимая составляющая электротехники.
Поиск по сайту: |
 , когда стало не хватать действительного числа, а именно при решении простейшего квадратного уравнения
, когда стало не хватать действительного числа, а именно при решении простейшего квадратного уравнения  , где «p» и «q» — действительные числа. При вычислении его корней по всем известным формулам, математики еще до XVI века сталкивались с проблемой отрицательного корня. В действительности, никто не мог объяснить какой смысл следует придавать этому выражению и, в следствие,
, где «p» и «q» — действительные числа. При вычислении его корней по всем известным формулам, математики еще до XVI века сталкивались с проблемой отрицательного корня. В действительности, никто не мог объяснить какой смысл следует придавать этому выражению и, в следствие, , надо заметить, что в математике знак мнимой части используется как «
, надо заметить, что в математике знак мнимой части используется как « 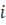 », но в электротехнике этим знаком обозначается ток, по этому было решено заменить его на «
», но в электротехнике этим знаком обозначается ток, по этому было решено заменить его на «  ». Знак «
». Знак «  » не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости «
» не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости « 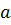 » и «
» и «  » координаты конца вектора тока, по мнимой и действительной оси.
» координаты конца вектора тока, по мнимой и действительной оси. запись результата вещественной и мнимой части через модуль «
запись результата вещественной и мнимой части через модуль «  » и аргумент «
» и аргумент «  »
» — получается путем применения формулы Эйлера к тригонометрической.
— получается путем применения формулы Эйлера к тригонометрической. — запись, не использующаяся для расчетов.
— запись, не использующаяся для расчетов. равняется не нулю, а скажем, 30
равняется не нулю, а скажем, 30  , :
, :
 ;
;


 ;
; и
и  , найдем
, найдем  и
и  .
. , значит:
, значит:
 и
и  через
через  и
и  :
:

 .
. ;
;  ,
, .
.