|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Спектральный анализ сигналов
Правила выполнения лабораторных работ
При подготовке к лабораторной работе каждый студент обязан: 1) заранее ознакомится с описанием очередной лабораторной работы; 2) ознакомиться с необходимым теоретическим материалом по учебникам, учебным пособиям и конспектам; 3) выполнить требуемые предварительные расчеты, начертить необходимые графики; 4) составить блок-схемы и функциональные схемы, исследуемые в лабораторной работе, продумать ход лабораторной работы; 5) подготовится к ответу на контрольные вопросы.
Выполнению каждой работы предшествует проверка подготовленности студента. Материалы домашней подготовки должны иметься у каждого студента. Если материалы, представленные студентом, или его ответы на вопросы признаны преподавателем неудовлетворительными, студент к выполнению работы не допускается и выполнить эту работу обязан во время дополнительных занятий, проводимых в конце семестра. При снятии кривых экспериментальные точки необходимо фиксировать в таблице и наносить на заранее заготовленный бланк. При зарисовке осциллограмм необходимо определять и фиксировать масштаб времени и уровней сигналов, их размерности. По окончании работы студент обязан представить результаты эксперимента преподавателю, выключить источник питания и приборы, привести в порядок рабочее место. Выполнение работ в лаборатории регламентируется также инструкцией по технике безопасности, ознакомление с которой подтверждается личной подписью студента.
Отчеты по лабораторной работе выполняются в тетради или на листочках и хранятся до окончания цикла лабораторных работ. По окончании цикла отчеты сдаются преподавателю на кафедру. Отчет должен содержать: 1) краткое содержание теории исследуемых процессов, а также необходимые предварительные расчеты и графики; 2) блок-схему лабораторного макета и функциональные схемы отдельных экспериментов; 3) результаты экспериментов в табличной и графической форме; 4) подробные графики выполнения отдельных экспериментов по указанию преподавателя; 5) основные выводы по лабораторной работе, включающие в том числе анализ расхождения теоретических и экспериментальных данных. На осциллограммах должны быть проведены оси координат и указаны масштабы времени и уровни сигналов. Небрежно составленный отчет может явиться причиной, по которой студент не получит зачета по выполненной работе.
ЛАБОРАТОРНАЯ РАБОТА 1 Спектральный анализ сигналов
Цель работы: изучение спектров сигналов различной формы и их сравнение с теоретически полученными зависимостями.
1. Общие сведения
1.1.Периодические сигналы
Важное место среди методов представления периодических сигналов занимает спектральный метод Фурье. При разложении периодических колебаний s(t) в ряд Фурье по тригонометрическим функциям в качестве ортогональных базисов принимаются следующие две системы [1]: …, 1; cosw1t; sinw1t; cos2w1t; sin2w1t; … ; cosnw1t; … (1.1) или …; exp(-j2w1t); exp(-jw1t); 1; exp(jw1t); exp(j2w1t);… (1.2)
В том случае, если используется система (1.1), то периодический сигнал записывается в виде ряда Фурье в тригонометрическом виде где
Если используется система (1.2), то получаем комплексный ряд Фурье
где
Между спектральными коэффициентами для базисов (1.1) и (1.2) справедливы простые соотношения: An=2|cn| и an=2cnc, bn=2cns. Имеются ряд полезных свойств рядов Фурье (см. [1]). Графическое представление рядов (1.3) и (1.4) приводит к линейчатому или дискретному спектру, т.к. последний состоит из отдельных линий, соответствующих дискретным частотам: 0, w1, w2=2w1, w3=3w1, … Вид спектра существенно зависит от формы периодического колебания. Найдем сначала теоретически линейчатые спектры для периодических колебаний, которые в дальнейшем исследуются экспериментально.
Пример 1.1. Разложим в ряд Фурье по формуле (1.3) колебание, соответствующее выходу однополупериодного, выпрямителя при воздействии на него синусоидального колебания (рис. 1.1).
Рис. 1.1.
Постоянная составляющая запишется в виде
Коэффициенты bn:
Пример 1.2. Разложим в ряд Фурье по формуле (1.4) колебание, аппроксимируемое функцией типа «меандр» (рис. 1.2). Рис. 1.2.
Поскольку эта функция нечетная относительно начала координат, то сnc=0;
Пример 1.3. Найдем по формуле (1.3) спектр сигнала, представленного на рис. 1.3: Рис. 1.3.
Произведя аналогичные предыдущим примерам вычисления, получим: a0/2=E/2; В итоге, сигнал представляется как
Пример 1.4. Разложение пилообразного колебания имеет вид
Пример 1.5. Разложение последовательности униполярных треугольных импульсов имеет вид
Пример 1.6. Разложение последовательности униполярных прямоугольных импульсов имеет вид
1.2.Непериодические сигналы
Непериодические сигналы отличаются от периодических тем, что не имеют периода повторения. Формально – это периодические сигналы с периодом Между формулами рядов и преобразований Фурье существует связь Пример 2.1. Симметричный прямоугольный импульс можно определить как
Пример 2.2. Симметричный треугольный импульс аналогично прямоугольному импульсу представляется спектром
Пример 2.3. Колоколообразный или гауссов импульс, определяемый как
Пример 2.4. Импульс вида Sinc(x), определяемый выражением
Пример 2.5. Сигнал вида e(t)=s(t)cos(w0t+j0) при относительно больших w0 относительно частотных составляющих спектра s(t) относится к узкополосным сигналам и обладает важными для практики свойствами. Применим к e(t) преобразование Фурье
Первый интеграл в правой части есть не что иное, как спектральная плотность функции s(t) при частоте w-w0, а второй интеграл – при частоте w+w0. Поэтому полученное выше выражение можно записать в виде
где Если s(t) – периодическое колебание, имеющее линейчатый спектр, то спектр узкополосного сигнала будет также линейчатым, расщепленным на две части и сдвинутым соответственно на -w0 и w0 по оси частот. Таким образом, при модуляции сигналом
высокочастотного сигнала cosw0t спектр колебания
будет представлять расщепленный спектр сигнала s(t), соответственно сдвинутый по оси частот на величину -w0 и w0. При модуляции исследуемого сигнала высокочастотным гармоническим колебанием cosw0t спектр результирующего колебания будет представлять расщепленный на два и сдвинутый соответственно на w0 и -w0 спектр модулирующего сигнала (рис. 1.4, а). Таким образом результирующий спектр будет иметь вид (рис. 1.4, b). Рис. 1.4 а Рис. 1.4 б
Если известна функция s(t), то определение параметров ряда Фурье с помощью выражений (1.3), (1.4) называется задачей спектрального анализа. Амплитудный спектр сигнала, т.е. зависимость амплитуд гармоник от частоты, может быть определен с помощью специального прибора – анализатора спектра. Если известны параметры ряда Фурье, то определяя сумму в правой части (1.3) для определенного числа членов, можно восстановить функцию s(t). Это будет задача синтеза сигнала (синтез по Фурье). Теоретически может определяться сумма бесконечного числа членов ряда (1.3). Тогда ряд Фурье восстанавливает функцию s(t) точно (кроме, может быть, отдельных точек). При суммировании же конечного числа членов ряда аппроксимация функции s(t) получается приближенной. Расхождение между функцией s(t) и суммой конечного числа членов ряда N тем больше, чем меньше N. Графики временных функций некоторых других распространенных периодических сигналов, а также правила расчета амплитуд An и начальных фаз qn, приведены в таблице 1.1.
2. Домашнее задание
Рассчитать и построить нормированные амплитудные спектры сигналов, указанных преподавателем. По оси ординат откладывать нормированную амплитуду гармоник (An/A1), по оси абсцисс – нормированную частоту n. Таблица 1.1.
3. Лабораторное задание
1. C помощью компьютерного анализатора спектра, построенного с использованием пакета LabView, получить и построить амплитудные спектры сигналов. 2. Используя данные о параметрах спектральных составляющих, указанных преподавателем сигналов, произвести с помощью компьютера синтез Фурье. Исследовать влияние числа суммируемых гармоник N на правильность восстановления формы сигнала.
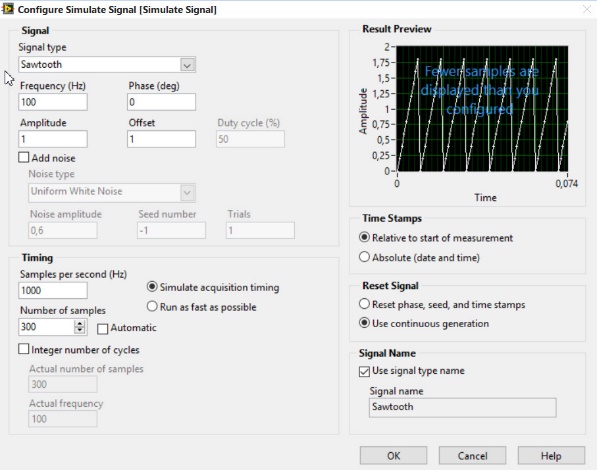
4. Описание лабораторного макета Лабораторный макет представляет собой компьютерную модель анализатора спектра, построенного в среде LabView и представлен на рис. 4.1.
Рис. 4.1.
Блок-схема модели имеет вид (см. рис. 4.2) и содержит блоки: Simulate Signal – источник моделируемого сигнала; Frequency, Offset, Phase, Amplitude – регулировки частоты, постянного уровня, фазы и амплитуды соответственно; Spectral Measurements – спектральный анализатор; Signal, Spectr – индикация спектра и сигнала.
Рис. 4.2.
Рекомендуемые параметры блоков представлены на скриншотах рис. 4.3. и рис. 4.4.
Рис. 4.3. Рис. 4.4.
5. Порядок выполнения работы. 5.1. Останавливая работу программы переходим к блок-схеме. 5.2. В источнике сигнала выбираем требуемый вид сигнала. 5.3. Запускаем программу. 5.4. Производим настройку сигнала с помощью органов регулирования параметрами сигнала. 5.5. Зарисовываем полученные данные (делаем скриншот). 5.6. Переходим к рассмотрению следующего вида сигнала. Для этого возвращаемся к 5.1. 5.6. Производим обработку полученных данных. Сюда входит: сравнение полученного спектра с теоретическим спектром, который в свою очередь получается из формул и расчетов; проверка выполнения свойств спектра, например, значения спектра на нулевой частоте, соотношения длительности сигнала и ширины спектра и т.д.
6. Содержание отчета
1. Графики расчетных и измеренных анализатором спектра амплитудных спектров сигналов. 2. Распечатки временных функций, полученных на компьютере. 3. Основные выводы по лабораторной работе, включающие анализ расхождения теоретических и экспериментальных данных.
7. Контрольные вопросы
1. Основные различия и характерные особенности спектров синусоидального, однополярного синусоидального колебания и колебания типа «меандр» одинаковой частоты. 2. Чем определяется ширина спектра колебания с амплитудной модуляцией? 3. Сходство и различие модулирующего, модулированного и модулируемого колебаний. 4. Можно ли считать исследуемые колебания узкополосными? Ответ обосновать, исходя из определения узкополосных радиосигналов. 5. Как влияет период повторения периодического сигнала на его спектр? 6. Как влияет число гармоник, участвующих в синтезе по Фурье, на форму получаемого сигнала? 7. Как влияет форма синтезируемого сигнала на число гармоник, которые необходимо использовать при его синтезе?
Рекомендуемая литература
1. Гоноровский И. С. Радиотехнические цепи и сигналы: учеб. Пособие для вузов / И.С. Гонорвский. 5-е изд., испр. и доп. М.:Дрофа, 2006. 719 с.: ил. 2. Баскаков С. И. Радиотехнические цепи и сигналы: Учеб. Для вузов по спец. «Радиотехника». 3-е изд., перераб. и доп. М.: Высш. шк., 2000. 462 с.: ил.
Рекомендуемая литература:
1. Гоноровский И. С. Радиотехнические цепи и сигналы: учеб. Пособие для вузов / И.С. Гонорвский. 5-е изд., испр. и доп. М.:Дрофа, 2006. 719 с.: ил. 2. Баскаков С. И. Радиотехнические цепи и сигналы: Учеб. Для вузов по спец. «Радиотехника». 3-е изд., перераб. и доп. М.: Высш. шк., 2000. 462 с.: ил.
Поиск по сайту: |
 (1.3)
(1.3)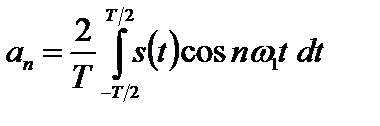 ;
;  ,
, ;
; 
 (1.4)
(1.4) ;
; 
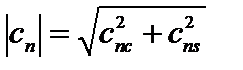 ;
;  ;
;  ;
;  .
. . Коэффициенты an:
. Коэффициенты an:  . После интегрирования получим
. После интегрирования получим .
. . После интегрирования получим
. После интегрирования получим 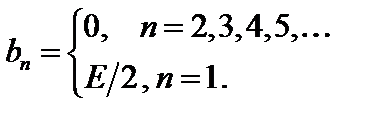 . Окончательно можно записать
. Окончательно можно записать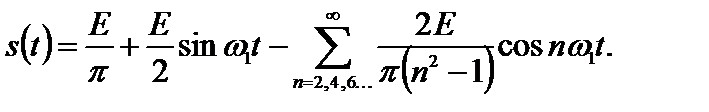
 , или
, или  . Окончательно можно записать
. Окончательно можно записать  .
.
 .
.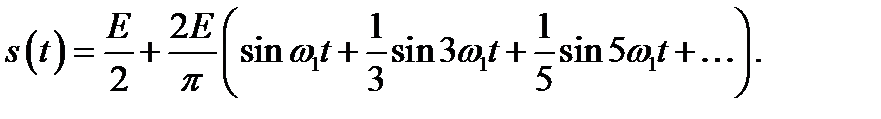



 . Формулы для рядов Фурье при этом трансформируются в преобразования Фурье
. Формулы для рядов Фурье при этом трансформируются в преобразования Фурье  , и обратные преобразования Фурье
, и обратные преобразования Фурье  . Полезно ознакомиться со свойствами преобразования Фурье [1], наиболее важные из которых: линейность; сдвиг сигнала по времени; изменение масштаба времени; дифференцирование сигнала; интегрирование сигнала; произведение сигналов; взаимозаменяемость частоты и времени в преобразованиях Фурье.
. Полезно ознакомиться со свойствами преобразования Фурье [1], наиболее важные из которых: линейность; сдвиг сигнала по времени; изменение масштаба времени; дифференцирование сигнала; интегрирование сигнала; произведение сигналов; взаимозаменяемость частоты и времени в преобразованиях Фурье. , где
, где  - спектр непериодического сигнала
- спектр непериодического сигнала 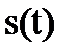 , а
, а  - спектр периодического сигнала
- спектр периодического сигнала  , полученного из
, полученного из 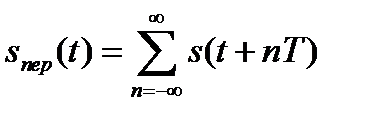 .
. . Спектральная плотность после вычисления интеграла Фурье имеет вид
. Спектральная плотность после вычисления интеграла Фурье имеет вид .
. .
. имеет спектр
имеет спектр  .
.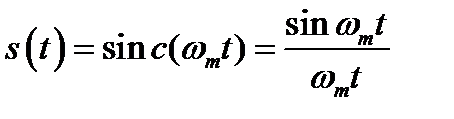 , имеет спектр
, имеет спектр 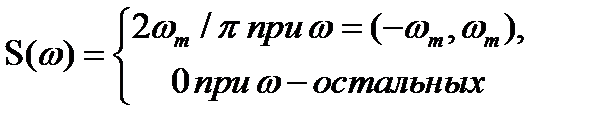 .
.
 ,
, – спектральная плотность колебания s(t).
– спектральная плотность колебания s(t).


 ?
?