 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пример расчета экстенсивного показателя
В районе А в текущем году было зарегистрировано 500 случаев инфекционных заболеваний, из них: эпидемического паротита — 60 случаев; кори — 100 случаев; прочих инфекционных заболеваний — 340 случаев. Вывод. В структуре инфекционных заболеваний доля эпидемического паротита составила 12%, кори — 20%, прочих инфекционных заболеваний — 68%. Б) экстенсивные -показатели удельного веса, структуры, характеризуют распределение явления на составные части, его внутреннюю структуру. Вычисляются экстенсивные показатели отношением части явления к целому и выражаются в процентах или долях единицы.
Экстенсивные показатели используются для определения структуры явления и сравнительной оценки соотношения составляющих его частей. Экстенсивные показатели всегда взаимосвязаны между собой, т. к. их сумма всегда равна 100 процентам: так, при изучении структуры заболеваемости удельный вес отдельного заболевания может возрасти: - при истинном росте числа заболеваний - при одном и том же его уровне, если число других заболеваний снизилось - при снижении числа данного заболевания, Если уменьшение числа других заболеваний происходит более быстрыми темпами. При анализе экстенсивный показатель следует применять с осторожностью и помнить, что им пользуются только для характеристики состава (структуры) явления в данный момент времени и в данном месте. Примеры использования в работе врача: лейкоцитарная формула; структура населения по полу, возрасту, социальному положению; структура заболеваний по нозологии; структура причин смерти. 5. Картограмма. Картограмма — это способ картографического изображения (но не карта), визуально показывающая интенсивность какого-либо показателя в пределах территории на карте (напр., плотность населения по областям). Данные могут наноситься на карту штриховкой различной густоты, окраской определенной степени насыщенности (фоновая картограмма) или точками (точечная картограмма).Картограммой считается графическое изображение статистических данных, сведенных по географическому принципу (напр., по административному делению), представляющее собой географическую карту, территории, которые окрашены (или заштрихованы) в соответствии с величиной исследуемого показателя, наблюдаемой на данной территории: ВидыВ зависимости от выбранного способа графического изображения различают фоновые и точечные картограммы. Фоновые картограммы строят путем окраски или штриховки, интенсивность которых пропорциональна величине показателя для данной территории.На точечных картограммах территориальное размещение изучаемого явления обозначают с помощью определенного числа точек. Как правило, к каждой картограмме прилагают краткое описание с указанием избранного способа картографического изображения и определенных градаций, а также всех условных обозначений. 6. Средние величины, их виды. Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.
Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности. Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака. Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором. Статистическая обработка методом средних величин заключается в замене индивидуальных значений варьирующего признака Например, индивидуальная выработка у 5 операционистов коммерческого банка за день составила 136, 140, 154 и 162 операции. Чтобы получить среднее число операций за день, выполненных одним операционистом, необходимо сложить эти индивидуальные показатели и полученную сумму разделить на количество операционистов:
Как видно из приведенного примера, среднее число операций не совпадает ни с одним из индивидуальных, так как ни один операционист не сделал 150 операций. Но если мы представим себе, что каждый операционист сделал по 150 операций, то их общая сумма не изменится, а будет также равна 750. Таким образом, мы пришли к основному свойству средних величин: сумма индивидуальных значений признака равна сумме средних величин.
Это свойство еще раз подчеркивает, что средняя величина является обобщающей характеристикой всей статистической совокупности. Средние величины широко применяются в различных отраслях знаний. Особо важную роль они играют в экономике и статистике: при анализе, планировании, прогнозировании, при расчете нормативов и при оценке достигнутого уровня. Средняя всегда именованная величина и имеет ту же размерность, что и отдельная единица совокупности. Виды средних величин Средние величины делятся на два больших класса: степенные средние и структурные средние Степенные средние:
Структурные средние:
Выбор формы средней величины зависит от исходной базы расчета средней и от имеющейся экономической информации для ее расчета. 7. Методы вычисления средних величин Для расчета средней величины необходимо построить вариационный ряд — т. е. ряд числовых измерений определенного признака, отличающихся по своей величине. Вариационные ряды бывают следующих видов: а) ранжированный, неранжированный; б) сгруппированный, несгруппированный; в) прерывный, непрерывный.
В зависимости от вида вариационного ряда используется тот или иной способ расчета средней. Средняя арифметическая для простого ряда, где каждая варианта встречается один раз, вычисляется по формуле: М =
, где
- знак суммы, V –отдельные значения вариант, n –число наблюдений. Средняя арифметическая взвешенная определяется по формуле: М=
, где
- знак суммы, V –отдельные значения вариант, n –число наблюдений, р – частота встречаемости вариант. Одним из наиболее простых и достаточно точных способов расчета средней арифметической является способ моментов, основанный на том, что алгебраическая сумма отклонений каждой варианты вариационного ряда от средней арифметической равна нулю. М= А + i
, где А – условно принятая средняя или мода, а- отклонение каждой варианты от условно принятой средней, р –частота встречаемости вариант, n –число наблюдений, i – интервал или расстояние между соседними вариантами. Основные свойства средней величины: 1) имеет абстрактный характер, так как является обобщающей величиной: в ней стираются случайные колебания; 2) занимает срединное положение в ряду (в строго симметричном ряду); 3) сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней величины используется для проверки правильности расчета средней. Она оценивается по уровню колеблемости вариационного ряда. Критериями такой оценки могут служить: амплитуда (разница между крайними вариантами); среднее квадратическое отклонение, показывающее, как отличаются варианты от рассчитанной средней величины; коэффициент вариации.
Средние величины делятся на два больших класса: степенные средние, структурные средние. К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая, средняя гармоническая и средняя квадратическая. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид: , где Xi – варианта (значение) осредняемого признака; m – показатель степени средней; n – число вариант. В зависимости от значения показателя степени m различают следующие виды степенных средних: при m = -1 – средняя гармоническая ; при m = 0 – средняя геометрическая ; при m = 1 – средняя арифметическая ; при m = 2 – средняя квадратическая ; при m = 3 – средняя кубическая . При использовании одних и тех же исходных данных, чем больше показатель степени m в вышеприведенной формуле, тем больше значение средней величины: . Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется правилом мажорантности средних. Взвешенная средняя считается по сгруппированным данным и имеет общий вид , где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; m – показатель степени средней; fi – частота, показывающая, сколько раз встречается i-e значение осредняемого признака. В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные
8. Среднее квадратическое отклонение. Среднеквадрати́ческое отклоне́ние — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок. Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины. Среднеквадратическое отклонение:
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной. 9. Динамические ряды, их виды. Динамический ряд — это ряд однородных статистических величин, показывающих изменение явления во времени. Динамический ряд может быть представлен абсолютными числами (изменение числа больных), средними величинами (среднее число лабораторных анализов за неделю) и относительными показателями (изменение рождаемости, заболеваемости, травматизма, обеспеченности врачами). Числа, из которых состоит динамический ряд, называются уровнями ряда. Анализ динамического (временного) ряда сводится к вычислению следующих показателей: абсолютного прироста (или снижения); темпа роста (или снижения); темпа прироста; значения 1% прироста. Абсолютный прирост Темп роста — это отношение последующего уровня к предыдущему, умноженное на 100%. Темп прироста является отношением абсолютного прироста (снижения) к предыдущему уровню, умноженным на 100%. Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста. Динамические ряды делятся на А) Простые (состоящие из абсолютных величин) - могут быть: 1) Моментными - состоит из величин, характеризующих явление на какой-то определенный момент (статистические сведения, обычно регистрируемые на начало или конец месяца, квартала, года) 2) Интервальными - Состоит из чисел, характеризующих явление за определенный промежуток времени (интервал) - за неделю, месяц, квартал, год (данные о числе родившихся, Умерших за год, число инфекционных заболеваний за месяц). Особенностью интервального ряда является то, Что его члены можно суммировать (при этом укрупняется интервал), или дробить. Б) Сложные (состоящие из относительных или средних величин). Динамические ряды могут подвергаться преобразованиям, целью которых является выявление особенностей изменения изучаемого процесса, а также достижение наглядности. Существуют различные виды рядов динамики, их можно классифицировать по следующим признакам. 1) В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных и производных показателей (относительных и средних величин). 2) В зависимости от того, как выражают уровни ряда состояние явления на определённые моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определённые интервалы времени (например, за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики. Моментные ряды в аналитической работе правоохранительных органов используются сравнительно редко. 10. Мода. Медиана. Медиана и мода в отличие от средней арифмети–ческой не погашают индивидуальных различий в зна–чениях варьирующего признака и поэтому являются дополнительными и очень важными характеристика–ми статистической совокупности. На практике они ча–сто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содер–жит некоторое количество единиц с очень большим или очень малым значением варьирующего признака. Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
где:
Медиана —это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда). При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
где:
11. Многофакторный дисперсионный анализ. Многофакторный анализ позволяет проверить влияние нескольких факторов на зависимую переменную. Линейная модель многофакторной модели имеет вид
где:
В рассмотренном выше простом примере вы могли бы сразу вычислить t-критерий для независимых выборок, используя соответствующую опцию модуля Основные статистики и таблицы. Полученные результаты, естественно, совпадут с результатами дисперсионного анализа. Однако дисперсионный анализ содержит гораздо более гибкие и мощные технические средства, позволяющие исследовать планы практически неограниченной сложности. 12. Методы эпидемиологических исследований. Методами изучения заболеваемости по данным выборочных исследований отдельных групп, популяций являются эпидемиологические методы. Эпидемиология - наука, изучающая особенности распространения и причины возникновения заболеваний в обществе с целью применения полученных знаний для решения проблем в здравоохранении.
Эпидемиологические исследования бывают единовременными, перспективными, либо ретроспективными. До настоящего времени исследование заболеваемости населения не проводится по единой методике, что затрудняет сравнение показателей заболеваемости. Однако любой показатель заболеваемости должен соответствовать следующим требованиям:
13. Аналитические эпидемиологические методы Для оценки гипотез в условиях риска, порождающих выявленные описательно-оценочными методами проблемы, используются аналитические эпидемиологические методы. Эти методы играют большую роль в определении направленной профилактики в соответствии не только с территориями, группами и временем риска, но и факторами риска. Выделяют два основных аналитических эпидемиологических метода: 1. Исследование типа "случай- контроль" 2. Когортное исследование. Исследование типа "случай- контроль" основывается на сопоставлении информации о подверженности действию изучаемого фактора больных и не больных данной болезнью. Достоверность исследования зависит от подбора групп сравнения, равноценности их по всем признакам, кроме изучаемого. В эпидемиологических исследованиях когорта-группа лиц с эпидемиологическим признаком. В когортном исследовании определяются интенсивные показатели заболеваемости в когортах, подверженных и подверженных фактору риска. В эпидемиологической диагностике когортные исследования на основе собранных данных об имевшей место заболеваемости называют ретроспективным эпидемиологическим анализом. Исследование с оценкой заболеваемости в динамике проводится в ходе оперативного эпидемиологического анализа. В результате когортного исследования выявляется непосредственный и относительный риск. Таким образом, аналитическая эпидемиология занимается поиском причины и следствия, отвечая на вопрос "почему и как возникло заболевание?". Аналитическая эпидемиология используется для количественного описания связи между воздействием и болезнью, а также для проверки гипотез о причинно-следственных связях.
Поиск по сайту: |

 Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности. некоторой уравновешенной средней величиной
некоторой уравновешенной средней величиной  .
.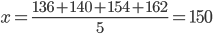 операций.
операций.




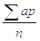


 — дисперсия;
— дисперсия;  — i-й элемент выборки;
— i-й элемент выборки;  — объём выборки;
— объём выборки;  — среднее арифметическое выборки:
— среднее арифметическое выборки:

 — значение моды
— значение моды — нижняя граница модального интервала
— нижняя граница модального интервала — величина интервала
— величина интервала — частота модального интервала
— частота модального интервала — частота интервала, предшествующего модальному
— частота интервала, предшествующего модальному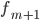 — частота интервала, следующего за модальным
— частота интервала, следующего за модальным , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
 — искомая медиана
— искомая медиана — сумма частот или число членов ряда
— сумма частот или число членов ряда - сумма накопленных частот интервалов, предшествующих медианному
- сумма накопленных частот интервалов, предшествующих медианному ,
, — результат измерения
— результат измерения  -го параметра;
-го параметра; — среднее для
— среднее для 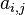 — систематическая ошибка измерения
— систематическая ошибка измерения  группе по методу
группе по методу  ;
;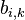 — систематическая ошибка измерения
— систематическая ошибка измерения  группе по методу
группе по методу 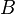 ;
;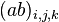 — систематическая ошибка измерения
— систематическая ошибка измерения 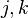 группе в силу комбинации методов
группе в силу комбинации методов  — случайная ошибка измерения
— случайная ошибка измерения