 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Принцип Даламбера и метод кинетостатики для материальной точки
Запишем дифференциальное уравнение движения несвободной материальной точки в виде ma = F + R, где F и R - равнодействующие активных сил и реакций связей, действующих на несвободную материальную точку. Перенесем член ma в правую часть уравнения и введем в рассмотрение вектор
равный произведению массы точки на величину ее ускорения, направленный противоположно вектору ускорения, и назовем введенный вектор даламберовой или просто силой инерции. Тогда основное уравнение динамики несвободной материальной точки примет вид
Силы F, R, Ф образуют систему сходящихся сил, а полученное уравнение выражает условие равновесия данной системы сил, что и составляет принцип Даламбера для материальной точки: в каждый момент движения материальной точки активные силы, реакции связей и сила инерции образуют уравновешенную систему сил. Ускорение точки можно разложить на составляющие. Поэтому и сила инерции раскладывается на соответствующие составляющие, например, в естественной системе координат Ф = Фτ + Фn, где составляющие силы инерции определяются так: Фτ = -maτ; Фn = -man. Даламберову силу инерции, введенную по формуле (1), не следует смешивать с реальными физическими силами. Даламберова сила инерции не имеет источника своего возникновения - другого тела. Она вводится условно в ходе математических преобразований основного уравнения динамики, чтобы придать уравнениям динамики вид условия или уравнения равновесия.
Следовательно, прикладывая силу инерции к движущейся материальной точке, мы можем говорить лишь об условном равновесии, приложенных к ней сил. Однако такое понимание динамического уравнения движения позволяет, используя уравнения равновесия статики, составлять динамические уравнения. Этот метод составления уравнений движения и называется методом кинетостатики. Например, спроектировав (2) на оси прямоугольной системы координат, можно получить три уравнения кинетостатики для материальной точки: которые представляют собой уравнения равновесия системы сходящихся сил, где к активным силам и реакциям связей, действующим на материальную точку, условно добавлена ее сила инерции. Так как принцип справедлив для любого мгновения времени, оси координат могут быть инерциальными или неинерциальными, неподвижными или подвижными. Важно лишь то, чтобы ускорение точки было определено в инерциальной системе координат или в абсолютном движении.
Поиск по сайту: |
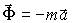 (1)
(1) (2)
(2) (3)
(3)