|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Поверхностные интегралы ⇐ ПредыдущаяСтр 2 из 2
def 1: Поверхность Φ называется полной, если фундаментальная последователь-ность точек из данной поверхности Φ сходится к точке принадлежащей Ф. def 2: Поверхность Φ называется ограниченной, если существует шар, содержащий все точки данной поверхности. Пусть задана поверхность Φ удовлетворяющая условиям: 1. гладкая; 2. без особых точек; 3. двух сторонняя; 4. полная; 5. ограниченная. и удовлетворяющая уравнению: x=x(u;v) y=y(u;v) (1) z=z(u;v)
На поверхности Ф определены и непрерывны 4 функции: f(x;y;z), P(x;y;z), Q(x;y;z),
Формула (2) верна и для всей площади Ф. Составим суммы:

cos x, cos y, cos z компоненты единичного вектора нормали.
def 3: Число def 4: Если существует конечный предел суммы def 5: Если существует конечный предел суммы
Если возьмем сумму
Если Ф кусочно-гладкая двухсторонняя поверхность x=x(u;v), y=y(u;v), z=z(u;v)
В частном случае, если поверхность Ф имеет вид z=z(x;y)
Этот интеграл не зависит от выбора стороны поверхности Ф. Если S гладкая двухсторонняя поверхность, S+ ее сторона, характеризуемая направлением нормали
При переходе к другой стороне S– поверхности S интеграл (4) меняет свой знак на противоположный. Моментом инерции части поверхности относительно осей координат выражаются поверхностными интегралами:
Координаты центра тяжести части поверхности можно найти по формулам:
Пример 1. Вычислить
Решение: Имеем
Тогда искомый интеграл преобразуется в двойной интеграл: Областью интегрирования D является круг
Пример 2. Вычислить
Решение: Расчленяем данный поверхностный интеграл на 3 слагаемых интеграла:
I1= I2= I3= I1= I3= Пример 3. Найти момент инерции полусферы Решение:
Областью интегрирования является проекция полусферы на плоскость xOy, т.е. круг
Замечание: внутри интеграл вычисляется с помощью подстановки
Пример 4. Вычислить координаты центра тяжести части плоскости z=x, огран. плоскостями x+y=1, y=0, x=0. Решение: Найдем площадь S указанной части плоскости
Задания: I.Вычислить поверхностный интеграл первого рода: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
II.Вычислить поверхностный интеграл второго рода: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
III.Найти: 1. Координаты центра масс однородной полусферы 2. Момент инерции однородного сегмента сферы 3. Координаты центра масс части однородной сферы 4. Момент инерции однородного параболоида 5. Момент инерции относительно плоскости xy части однородного конуса 6. Координаты центра масс верхней полусферы 7. Момент инерции однородной поверхности 8. Координаты центра масс части однородной поверхности 9. Момент инерции части однородной верхней полусферы 10. Координаты центра масс части однородного конуса Ответы:
Литература 1. Зорич В.А. Математический анализ. т.2–М: Наука, 1984, стр. 113-165 2. Кудрявцев Л.Д. Курс математического анализа. т.2–М: Высшая школа, 1989, стр. 286-490 3. Никольский С.М. Курс математического анализа. т.2–М: Наука, 1991, стр. 7-85 4. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М: Наука, 1990, стр. 406-471 5. Данко П.Е., Высшая математика в упражнениях и задачах: Учебное пособие для студентов ВТУЗов. М: Высшая школа, 1986, стр. 6-66 6. Гусак А.А. Задачи и упражнения по высшей математике. т.2 Минск: Высшая школа, 1988, стр. 42-122 7. Миронский В.П. Сборник задач по высшей математике. стр. 233-248 8. Берман Г.Н. Сборник задач по курсу математического анализа М: Наука, 1985, стр. 213-247
Поиск по сайту: |
 или
или  (1')
(1') . Гладкими или кусочно гладкими кривыми разбиваем Ф на частичные поверхности
. Гладкими или кусочно гладкими кривыми разбиваем Ф на частичные поверхности  . Рассмотрим точку
. Рассмотрим точку  . Через
. Через  обозначим площадь
обозначим площадь 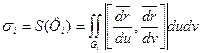
 , где
, где 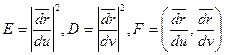 (2)
(2) вектор нормали
вектор нормали 

 называется пределом интегральных сумм
называется пределом интегральных сумм  при А→0, если для
при А→0, если для  что для
что для  разбиения Ф на Фi , диаметр разбиения которого
разбиения Ф на Фi , диаметр разбиения которого  и для
и для  выполняется неравенство
выполняется неравенство 
 то говорят что функция f(x,y,z) интегрируема по поверхности Ф, а число
то говорят что функция f(x,y,z) интегрируема по поверхности Ф, а число  называется поверхностным интегралом первого рода от функции f(x,y,z) и обозначается
называется поверхностным интегралом первого рода от функции f(x,y,z) и обозначается  где
где  дифференциал поверхности.
дифференциал поверхности.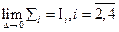 , то этот предел
, то этот предел 
 , то получи общий поверхностный интеграл второго рода:
, то получи общий поверхностный интеграл второго рода:
 и f(x,y,z) функция определена и непрерывна в точках поверхности Ф, то
и f(x,y,z) функция определена и непрерывна в точках поверхности Ф, то , где (3)
, где (3)
 однозначная, непрерывно дифференцируемая функция, то
однозначная, непрерывно дифференцируемая функция, то
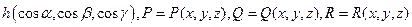 три функции, определенные и непрерывные на поверхности S, то
три функции, определенные и непрерывные на поверхности S, то (4)
(4)

 , где S часть конической поверхности
, где S часть конической поверхности  , заключенной между плоскостями z=0, z=1.
, заключенной между плоскостями z=0, z=1.
 .
.


 , где T внешняя сторона части эллипсоида
, где T внешняя сторона части эллипсоида  , расположенной в первом октанте.
, расположенной в первом октанте. и пользуясь уравнением поверхности Ф, и формулой
и пользуясь уравнением поверхности Ф, и формулой





 относительно оси Oz
относительно оси Oz
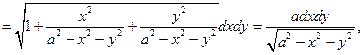

 , а поэтому, переходя к полярным координатам, получим:
, а поэтому, переходя к полярным координатам, получим:
 .
.





 лежащая внутри цилиндра
лежащая внутри цилиндра 
 лежащая внутри цилиндра
лежащая внутри цилиндра 
 , лежащая между конусом
, лежащая между конусом  и параболоидом
и параболоидом 
 лежащая между плоскостями
лежащая между плоскостями 
 , лежащая вне гиперболоида
, лежащая вне гиперболоида 
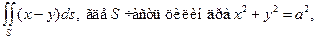 лежащая внутри цилиндра
лежащая внутри цилиндра 

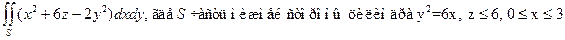

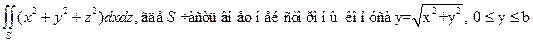







 .
. плотности ρ относительно Oz.
плотности ρ относительно Oz. .
. плотности ρ относительно Oz.
плотности ρ относительно Oz. массой M.
массой M. плотности ρ относительно Oz.
плотности ρ относительно Oz. плотности ρ, лежащей внутри цилиндра
плотности ρ, лежащей внутри цилиндра  относительно плоскости.
относительно плоскости. .
. 2.
2.  3.
3.  4.
4.  5.
5. 
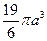 7.
7.  8.
8.  9.
9.  10.
10. 
 2. 324
3. 88
4.
2. 324
3. 88
4.  5.
5. 
 7.
7.  8.
8.  9.
9.  10.
10. 
 2.
2.  3.
3.  4.
4.  5.
5. 
 7.
7.  8.
8.  9.
9.  10.
10.