 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Алгоритм классификации с использованием комитетов старшинства
В статье [126] М. Осборн ввел понятие комитета старшинства для разделения двух классов объектов и предложил алгоритм построения комитета, работающий с двоичными векторами. Сотрудником ИММ УрО АН СССР Н. Г. Белецким понятие комитета старшинства было обобщено па случай произвольного числа классов и разработан алгоритм построения такого комитета [12]. Алгоритм ориентирован на обработку векторов, координатами которых являются произвольные вещественные числа. В соответствии с определением, данным в [12], комитет старшинства, предназначенный для разделения ранжированы от 1 до Для классификации произвольного вектора Другими словами можно сказать, что член комитета В качестве обучающей информации при построении комитета используется множество комитета изменяется не только число его членов, а изменяются (корректируются) и сами эти члены. Текущее состояние комитета в процессе его построения в [12] предложено называть приближением комитета. Коррекция приближения представляет собой процедуру, предусматривающую коррекцию некоторых его членов по определенному правилу. Коррекцией
где станта, называемая возрастом члена комитета и имеющая перед первой коррекцией значение
Сопротивлением члена комитета названа величина
где Значения сопротивлений используются в алгоритме при принятии решений относительно включения в приближение новых членов. Понятие комитета старшинства и алгоритм его построения можно упрощенно проиллюстрировать на примере разделения двух множеств на плоскости. Элементы множеств обозначим соответственно «крестиками» и «ноликами» и пронумеруем (см. рис. 1.6, а). На рис. 1.6,б, 1.6, в и 1.6, г показана последовательность построения разделяющего комитета старшинства, состоящего из четырех членов. Каждому члену комитета на рисунках соответствует прямая линия. Около каждой прямой указан номер члена комитета и его тип (в скобках). Значение ранга члена комитета совпадает с его номером. Черточками на прямых отмечены положительные полуплоскости, в которых члены комитета голосуют.
Рис. 1.6. Пример построения комитета старшинства При построении первого члена комитета (рис. 1.6, б) алгоритм стремится отделить по возможности большее число объектов какого-то одного класса. В данном случае были отделены «нолики» с номерами 6, 9 и 11. При построении второго члена комитета эти объекты во внимание не принимаются. Построение выполняется с учетом того же принципа: отделить по возможности большее число объектов одного класса. С помощью прямой, соответствующей второму члену комитета, таким образом отделяются «крестики» с номерами 3, 4 и 5 (рис. 1.6, в). На рис. 1.6, г изображен уже полностью сформированный комитет. Добавились, как видно, еще два члена. При этом третий член комитета строился так же, как первые два, но без учета ранее отделенных объектов 3, 4, 5, 6, 9, 11. С помощью этого члена комитета «нолики» с номерами 7, 8, 10 отделились от «крестиков» 1 и 2. И, наконец, четвертый член комитета построен для того, чтобы, согласно определению комитета, правильно классифицировались «крестики» с номерами 1 и 2. Следует еще раз подчеркнуть, что приведенный пример лишь приблизительно иллюстрирует алгоритм построения комитета. Так, на рисунках показано, что члены комитета строятся строго последовательно. В действительности же процесс построения является параллельно-последовательным. При этом включение в комитет новых членов сочетается с коррекцией уже построенных. Пользуясь рисунком 1.6, г, поясним, как осуществляется классификация объектов с помощью полученного комитета. Предположим, требуется классифицировать объект «звездочка» с номером 12, не и пользовавшийся при построении комитета. Для этого сначала необходимо выяснить, лежит ли классифицируемый объект в положительной полуплоскости, определяемой первым, т. е. старшим по рангу, членом комитета. Этот факт устанавливается вычислением соответствующего скалярного произведения. В данном случае оказалось, что в положительной полуплоскости первого члена комитета классифицируемый объект не расположен. Таким образом этот член комитета воздерживается от голосования. Второй член комитета также воздерживается от голосования. И, наконец, третий член комитета голосует за данный объект. Согласно приведенному в начале раздела алгоритму классификации, относим объект «звездочка» ко второму классу, поскольку значение типа третьего члена комитета равно двум. Рассмотренный алгоритм реализован в пакете в виде программного модуля MK.S. Модуль организован таким образом, что при построении комитета используются обучающие векторы с нормированными признаками, а полученный комитет преобразуется к виду, пригодному для классификации векторов с ненормированными признаками. Выходная информация. Модуль MKS выдает на печать следующую информацию: 1) число векторов, участвовавших в обучении; 2) процент правильного распознавания векторов 3) число членов комитета; 4) число векторов материала обучения, отсекаемых каждым членом комитета, и количество допущенных при этом ошибок классификации;
5) проценты правильного распознавания векторов проверочной выборки (общий и по классам); 6) результаты классификации векторов рабочего распознавания.
Процесс решения задачи РО 1. Сформулировать задачу ИИ в терминах распознавания образов. Определить тип задачи РО: задача обучения с учителем, задача поиска информативных признаков или задача обучения без учителя. 2. После того, как определена задача РО, следует выбрать компактное признаковое описание. 3. Подготовить входные данные. Смотри ниже особенности описание входных данных. 4. Затем входные данные должны быть введены в программу КВАЗАР, в процессе, которого исправляются ошибки в данных. 5. Выбирая из главного меню КВАЗАРа необходимые алгоритмы, решить задачу.
Подготовка данных для пакета КВАЗАР. Файл данных обычно бывает подготовлен в символьном виде массива – матрица “ объект - признаки” При решении задачи обучения по прецедентам (фактам) в входном файле должен соблюдаться следующий порядок векторов – объектов: 1. векторы известной принадлежности, представленные на обучение (из них пакет автоматически или на основе указаний пользователя может сформировать обучающую и проверочные выборки); при этом сначала следуют векторы 1 класса – образа, затем второго и т.д.; 2. векторы, предъявленные для рабочего распознавания (при наличии) Работая с пакетом КВАЗАР, нумеровать векторы не следует. Номер вектора определяется его местом в файле (массиве) обрабатываемых данных.
Требования пакета КВАЗАР к подготовке входного файла 1. каждая запись – объект “ n”- мерный вектор состоит из признаков вещественных чисел, которые разделяются пробелом или запятой, в конце описания вектора ставится символ “;” . 2. Набор следующего вектора -- новая запись, т.е. новая строка. 3. В начале вектора можно указывать имена векторов, которые отделяются от признаков символом “:”. 4. Данные должны быть набраны в “DOS” кодировке в любом редакторе, например БЛОКНОТ шрифт Terminal . 5. Имя файла должно состоять из 8 латинских символов – “ группа и ваш номер по списку”. Файла должен быть записан для удобства работы в каталог DATA пакета КВАЗАР. Пример. Файл - I1601001.dat I16010 – группа 01- ваш номер по списку.
ИМЯ : 2 2 9 1. 1. 6. 1. 2.;
Поиск по сайту: |
 непересекающихся множеств векторов
непересекающихся множеств векторов  ,
,  , представляет собой совокупность весовых векторов
, представляет собой совокупность весовых векторов  . Члены комитета
. Члены комитета (1 — самый высокий ранг,
(1 — самый высокий ранг,  — самый низкий) и характеризуются типом
— самый низкий) и характеризуются типом 
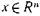 с помощью комитета старшинства последовательно вычисляются скалярные произведения вектора
с помощью комитета старшинства последовательно вычисляются скалярные произведения вектора 
 на векторы
на векторы  и т. д. до получения первого положительного скалярного произведения. Если первым таким произведением является
и т. д. до получения первого положительного скалярного произведения. Если первым таким произведением является 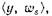 относим вектор
относим вектор  к классу
к классу  . Если же все
. Если же все  скалярных произведений отрицательны, относим вектор
скалярных произведений отрицательны, относим вектор  к классу
к классу  .
.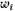 голосует за вектор
голосует за вектор  , еслиили воздерживается от голосования, если
, еслиили воздерживается от голосования, если  Если все члены комитета воздерживаются, то считается проголосовавшим член самого низкого ранга, т. е.
Если все члены комитета воздерживаются, то считается проголосовавшим член самого низкого ранга, т. е.  В противном случае решающее значение имеет, как показано выше, голос наиболее высоко ранжированного члена. Такая логика процедуры голосования и определила название «комитет старшинства».
В противном случае решающее значение имеет, как показано выше, голос наиболее высоко ранжированного члена. Такая логика процедуры голосования и определила название «комитет старшинства». где
где  . Комитет строится последовательно в том смысле, что сначала в него включается всего один член
. Комитет строится последовательно в том смысле, что сначала в него включается всего один член 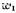 , а затем число членов увеличивается по мере необходимости. Причем в процессе построения
, а затем число членов увеличивается по мере необходимости. Причем в процессе построения -го члена комитета в ответ на предъявление вектора
-го члена комитета в ответ на предъявление вектора  из класса
из класса  называется изменение вектора
называется изменение вектора  , определенное последовательностью действий:
, определенное последовательностью действий: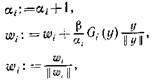
 — знак присваивания значения;
— знак присваивания значения;  — кон-
— кон- — константа,
— константа,
 на векторе
на векторе 

 — возраст члена комитета,
— возраст члена комитета,  — положительная константа.
— положительная константа.