 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лабораторна робота № 41-1
Дослідження фізичного маятника
Мета роботи. Дослідити згасаючі коливання фізичного маятника і за виміряним числом повних коливань Nt і часу релаксації t обчислити: · сталу згасання g, · коефіцієнт опору r, · логарифмічний декремент згасання l , · добротність коливальної системи Q, оцінити коефіцієнт тертя кочення. Теоретичні відомості:
Використовуючи другий закон Ньютона для обертового руху, рівняння коливань можна записати так:
де J ¾ момент інерції тіла. Вектори
В канонічному вигляді рівняння (2.41) можна записати так
де Розв'язок (3.41) шукаємо підстановкою Ейлера j=elt. Знайдемо перші дві похідні від j по часу
Підставляючи похідні (4.41) в (3.41), одержимо: elt ( l2 + 2gl + w02 ) = 0. (5.41) Квадратне рівняння l2 + 2gl + w02 = 0 в (5.41) називається характеристичним. Його розв'язок
дає два фундаментальні розв'язки диференціального рівняння j1 = exp(l1t), j2 = exp(l2t), (7.41) з яких утворюється загальний розв'язок. Загальним розв'язком однорідного рівняння (3.41) буде лінійна комбінація фундаментальних розв'язків j = Аexp(l1t) + Bexp(l2t) (8.41) з дійсними коефіцієнтами А, В. Якісно розрізняють два випадки руху маятника: 1) При g > w0 ¾ аперіодичний рух. При цьому l1,l2 < 0 ¾ дійсні числа. Функція j є спадною функцією часу (l1,l2<0) і описує асимптотичне, в експоненційній залежності від часу, повернення маятника в стан рівноваги. При цьому коливальний рух не здійснюється. 2) Якщо g < w0, маятник буде здійснювати коливальний рух. При цьому l1 = - g+іw, l2 = - g-іw, (9.41) де і = j = e-gt(Aeiwt + Be-iwt) (10.41) з комплексними коефіцієнтами А, В. Для знаходження величин А та В зауважимо, що функція j є дійсною функцією часу, і за цим вона має дорівнювати своїй комплексно спряженій функції j = j* Þ e-gt(Aeiwt+Be-iwt) = e-gt(A*e-iwt +B*eiwt). (11.41) Прирівнюючи в (11.41) коефіцієнти при однакових експонентах, одержимо В=А*. Для зручності комплексну сталу А візьмемо в експоненціальному вигляді А = а0eia/2, де а0 ¾ дійсна величина. Тепер j = а0/2·e-gt (ei(wt+a) +e-i(wt+a)) (12.41) і, користуючись формулою Ейлера e±ix = cosx ± i×sinx, вираз в дужках запишемо у вигляді: j = j = j0(t)×cos(wt+a). (13.41) В (13.41) j0(t) = a0e-gt ¾ амплітуда коливань ¾ спадна функція часу, Ф = wt+a ¾ фаза коливань, Ф0 = a ¾ початкова фаза.
Поиск по сайту: |
 Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор
Фізичний маятник ¾ макроскопічне тіло, що здійснює малі періодичні коливання. Вісь обертання маятника О зміщена відносно центра мас тіла Oc на вектор 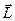 . Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту
. Коливання визначаються кутом j відхилення тіла від положення рівноваги. Ці коливання здійснюються в загальному випадку під дією моменту  зовнішніх сил
зовнішніх сил  , моменту сили тяжіння
, моменту сили тяжіння 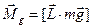 та моменту сил опору
та моменту сил опору 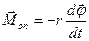 , де
, де  ¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj » j і Мg = mgLj.
¾ коефіцієнт опору. Величину моменту сили тяжіння можна записати у вигляді: Мg = mgLsinj. Для малих коливань маятника маємо sinj » j і Мg = mgLj.  , (1.41)
, (1.41) лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі:
лежать на одній прямій, а тому, взявши за додатній напрямок кутового прискорення, векторне рівняння можна записати в алгебраїчній формі: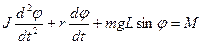 . (2.41)
. (2.41) , (3.41)
, (3.41) ¾ коефіцієнт згасання коливань,
¾ коефіцієнт згасання коливань,  , w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p
, w0 ¾ частота вільних незгасаючих коливань. Період малих власних коливань маятника T0 = 2p/w0 і T0 = 2p  , де lпр =
, де lпр =  ¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41)
¾ приведена довжина фізичного маятника. Для прикладу розглянемо вільні згасаючі коливання фізичного маятника. Рівняння згасаючих коливань є однорідним диференціальним рівнянням, яке враховує сили опору (3.41) elt,
elt,  = l2elt. (4.41)
= l2elt. (4.41) ,
, 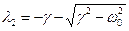 (6.41)
(6.41) ¾ уявна одиниця, w =
¾ уявна одиниця, w = 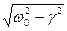 ¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд:
¾ частота вільних згасаючих коливань. Загальний розв'язок буде мати вигляд: а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ
а0e-gt [cos(wt+a)+i×sin(wt+a)+cos(wt+a)-i×sin(wt+a)] Þ