 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
От температуры для металлического
резистивного датчика.
Такие датчики в большинстве случаев изготавливаются с сопротивлением 100 Ом при 0оС, обладают положительным ТКС и являются достаточно точными(хорошая повторяемость результатов). Термисторы
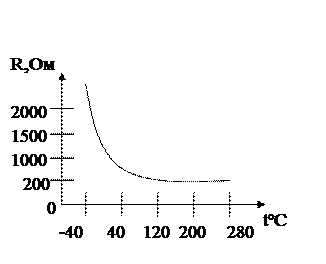
Термисторы- это термочувствительные резисторы, изготовленные из полупроводниковых монокристаллов германия и кремния или из других поликристалических полупроводниковых материалов. Большинство же выпускаемых полупроводниковых термисторов характеризуются высоким сопротивлением и большой величиной отрицательного ТКС - 3...6 % оС-1, что примерно в 10 раз больше, чем у платиновых и никелевых датчиков. Однако повышенная чувствительность сопровождается потерей линейности. Зависимости сопротивления от температуры для термисторов:
R =
где А - константа; W - энергия разрыва валентной связи; В - константа материала; То – исходная температура. В этом случае температурный коэффициент, согласно выражению (1), оказывается равным
a = - В / Т2, (4)
т.е. зависит от температуры и, следовательно, для каждой температуры имеет свое значение. Температурная зависимость сопротивления для таких датчиков приведена на рисунке 2:
3.Физические принципы работы резистивных термодатчиков
Как металлы, так и полупроводники, на основе которых изготавливаются резистивные датчики температуры, являются кристаллами. Внешнее электрическое поле Е, приложенное к однородному кристаллу, вызывает электрический ток, обусловленный перемещением свободных носителей заряда, плотность которого j = s . E, (5)
Коэффициент пропорциональности s называется удельной электрической проводимостью вещества. Под действием электрического поля с напряженностью Е свободные электроны в кристалле должны двигаться в одном направлении с постепенно нарастающей скоростью υ, однако в реальности этого не происходит из-за того, что тепловые колебания атомов кристаллической решетки затрудняют (мешают)направленному движению электронов против электрического поля Е. При этом траектория движущихся электронов искривляется, т.е. они рассеиваются. Количественной мерой рассеивания служит длина свободного пробега электрона L – среднее рассеивание, проходимое электроном между двумя столкновениями (актами взаимодействия) с колеблющимися атаками кристаллическими решетки. Чем больше величина L, тем меньше степень рассеяния и наоборот, чем меньше величина L , тем больше степень рассеивания. Таким образом, при совместном действии электрического поля и рассеяния движение электронов в кристалле происходит с конечной средней скоростью направленного движения υ, которая пропорциональна электрическому полю Е:
υ = bE (6)
Величина b , равная средней скорости носителя в поле с напряженностью 1 В/см, называется подвижностью носителей заряда. Ее размерность, согласно (6), [b] = [ n ] / [ Е ] = = [ см2 / В . с ]. Средняя скорость n, подвижность b и, следовательно, удельная электрическая проводимость, равная
s = еnb (7)
(где е - заряд электрона, n - концентрация носителей заряда) зависят от числа и характера актов рассеяния, т.е. в значительной мере определяются длиной свободного пробела носителей заряда. Удельное сопротивление r связано с проводимостью выражением
r = 1 / s = 1 / enb (8)
Из (8) следует, что температурная зависимость r, а значит, и полного электросопротивления R = r . l / S , определяется зависимость от температуры величин n и b . Для металлов, как правило, n = соnst, следовательно, за температурную зависимостьr отвечает изменение b с температурой. С ростом температуры увеличиваются амплитуды тепловых колебаний атомов решетки, что приводит к увеличению рассеяния носителей заряда (электронов). Поэтому при увеличении температуры уменьшается длина свободного пробега L и, как следствие этого, снижается величина подвижности b носителей заряда (b, L). С учетом этого на основании выражения (8) можно сделать вывод, что сопротивление чистого металла будет тем больше, чем интенсивнее тепловое движение атомов, которое увеличивается с ростом температуры. С другой стороны, согласно теории, при стремлении температуры к абсолютному нулю сопротивление чистого металла должно стремиться к нулю. Это подтверждается экспериментально. По своему строению полупроводники, как и металлы, являются кристаллами. Однако в отличии от металлов они имеют меньшую плотность упаковки атомов в кристаллической решетке. При плотной же упаковке атомов (металлы) из-за сильного электрон – электронного взаимодействии близко расположенных соседних атомов часть электронов отрывается от своих атомов и становится общей для всего кристалла в целом. Свободные электроны могут участвовать в проведении электрического тока, и по этому они называются электронами проводимости. В металлах электроны проводимости существуют изначально, а их концентрация постоянна и не зависит от температуры кристалла. При менее плотной упаковке атомов (их «далеком» расстоянии друг от друга) в полупроводниках электрон-электронное взаимодействие соседних атомов существенно ниже чем в металлах. В связи с этим свободные электроны не возникают, а реализуется чисто ковалентная связь между атомами с участием электронов. Поскольку все электроны связанны, то казалось бы, полупроводники не должны иметь электронов проводимости, и по этой причине не могут проводить электрический ток. Однако практика этого не подтверждает: полупроводники проводят электрический ток, но, правда, хуже чем металлы. Кстати говоря, поэтому они и называются полупроводниками (в сравнении с металлами - проводниками). Этот установленный на практике факт свидетельствует, что полупроводники все же имеют электроны проводимости, но в меньшей концентрации n. Позже было найдено, что на это есть две причины: 1) собственная проводимость и 2) примесная проводимость. В соответствии с первой причиной из-за тепловых колебаний атомов в кристаллической решетке всегда существует некая зависящая от температуры вероятность разрыва ковалентной связи между атомами, которая сопровождается появлением свободных электрона и «дырки» (разорванная ковалентная связь). Причем эти оба носителя заряда (электрон и «дырка») могут перемещаться по кристаллу, но с разной скоростью и, следовательно, участвовать в проведении электрического тока. Действительно, разорванная связь может захватить электрон с ковалентной связи соседнего атома и т. д., что равносильно перемещению разорванной ковалентной связи («дырки») по кристаллу. Поэтому собственная концентрация n свободных носителей заряда в полупроводниках будет равна сумме концентрации электронов ne и дырок nр : n = ne + np (9) В чистом полупроводнике ne = np и ne ˜ eW/2кТ (10) , где W-энергия, необходимая для разрыва ковалентной связи (энергия связи валентного электрона в атоме), к - постоянная Больцмана и Т- абсолютная температура. Из (10) следует, что с ростом температуры ne резко(по экспоненте) увеличивается(чего не было в металлах). Увеличение же n , согласно выражения (8), приводит к очень быстрому уменьшению электросопративления чистого полупроводника с ростом температуры (см. рис. 3). Таким образом, температурная зависимость сопротивления чистых полупроводников (например, Si и Ge) обусловлена в основном появлением дополнительных свободных носителей заряда (электронов и дырок) с ростом температуры кристалла. В соответствии со второй причиной (примесная проводимость) в кристаллах полупроводников могут изначально присутствовать или намеренно вводиться в чистый кристалл путем его легирования различные примеси, которые вносят в кристалл электроны или дырки проводимости. Например, если кристалл чистого кремния залегировать пятивалентной примесью фосфора, то атомы фосфора P, встраиваясь в решетку, состоящую из четырехвалентных атомов Si, отдадут свой пятый валентный электрон, который станет свободным. Если атомов фосфора достаточно много, то кристалл кремния приобретет ярко выраженную электронную проводимость, а температурная зависимость его электросопротивления будет схожа с таковой для металлов. Аналогичным образом введение трехвалентного бора (В), вызовет появление ярко выраженной дырочной проводимости, так как атомы бора (В) будут захватывать из решетки по одному электрону, т.е. вносить «дырки» в исходный кристалл. Рис.3 Рабочая характеристика германиевого датчика Если же кремний является чистым (нелегированным), то он, в соответствии с выражениями (3 и 8), изначально имеет такую же рабочую характеристику (электросопротивление уменьшается почти по экспоненте с ростом температуры).
Термопары
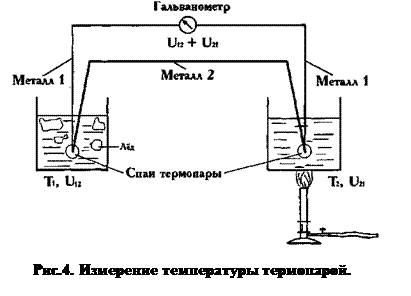
Термопара - это устройство, состоящее из двух соединенных на одном из концов разнородных металлических проводов, например, меди и медно-никелевого сплава, железа и медно-никелевого сплава или платины и платинородиевого сплава. Место соединения проводов называется спаем (на практике - это сварной контакт). Если температура спая и свободных концов различны, то между последними возникает электродвижущая сила (ЭДС), зависящая от разности температур. Соединив между собой две такие термопары, получаем так называемую дифференциальную термопару или полный датчик, т.е. кольцо, состоящее из двух металлов. Если теперь один спай поместить при 0оС (тающий лед), а второй - в среду с температурой, отличной от 0оС, то между спаями возникает ЭДС (Рис.4) . Термоэлектрические датчики температуры (термопары) основаны на эффекте Зеебека, суть которого состоит в следующем. Если два проводника из разнородных металлов соединить друг с другом концами, так что образуется замкнутая цепь (рис. 5), а образовавшиеся контакты А и В поместить при различных температурах, то в этой замкнутой цепи будет течь ток. При сохранении разницы в температурах двух контактов (спаев) ток будет течь постоянно. Электродвижущая сила (ЭДС), вызывающая этот ток, называется термоЭДС Зеебека. И наоборот при пропускании тока по такой замкнутой цепи один из контактов (спаев) будет нагреваться, а другой – охлаждаться (эффект Пельтье). Последнее используется для создания холодильников.
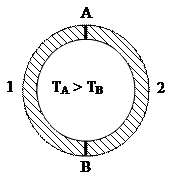
Рис.5. Схема термопары, образованной двумя разнородными металлами 1 и 2 В зависимости от вида термопары величина этой ЭДС составляет от 7 до 75 мкВ / оС. ЭДС термопары связана с разностью температур спаев практически линейной пропорциональной зависимостью. График выходного напряжения термопары как функция температуры приведен на рис.6
Рис. 6. Зависимость ЭДС от разности температур спаев для типичной термопары Основным достоинством металлических датчиков и термопар является возможность их использования в широком интервале температур. Рассмотрим физический принцип работы термопары. В приконтактной области (рис.5) двух разнородных (т.е. с разными концентрациями электронов) металлов или полупроводников возникают диффузионные потоки электронов из одного материала в другой. В результате этого контактирующие материалы заряжаются в области спая противоположными зарядами А: положительный заряд приобретет тот металл (полупроводник), который первоначально имел более высокую исходную концентрацию электронов, а отрицательный заряд получит другой металл (полупроводник), куда продиффундировали электроны из первого. Такое разделение зарядов приведет к возникновению внутренней контактной разности потенциалов UА, которая будет увеличиваться при сохранении разности диффузионных потоков. Однако по мере достижения определенной величины UА образующаяся контактная разность потенциалов уравняет диффузионные потоки электронов в обоих направлениях, и наступит динамическое равновесие, для которого характерно равенство электрохимических потенциалов соприкасающихся материалов (m1=m2 или Dm=0). UA=
С учетом (11) из условия равенства электрохимических потенциалов соприкасающихся металлов не сложно получить выражение для ЭДС термопары, просуммировав контактную разность потенциалов в областях спаев А и В, обходя кольцо в одном направлении:
eТ = UA + UB= = где е- заряд электрона, к- постоянная Больцмана
Из (12) видно, что величина термоЭДС зависит от различий концентраций свободных электронов в металлах (Ln В связи с этим для повышения термоЭДС выбирают пары металлов с большой разницей концентраций электронов и объединяют несколько термопар в термобатарею.
Поиск по сайту: |
 eW/2кТ или в другой форме записи R = Rо ехр [В ( 1/Т - 1/То ) ], (3)
eW/2кТ или в другой форме записи R = Rо ехр [В ( 1/Т - 1/То ) ], (3)

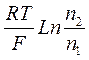 ,(11)
,(11)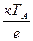 Ln
Ln  +
+ 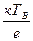 Ln
Ln 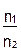 =
= 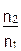 =
= Ln
Ln