|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Деформація полімерних матеріалів
Лабораторна робота № 1
Мета роботи: навчитися визначати значення загальної граничної деформації полімерних матеріалів та розподіл її по видах.
Теоретичні відомості: Під деформацією розуміють зміну форми об’єкту, яка не супроводжується зміною його об’єму та фазовими переходами. Для виникнення деформації до об’єкту повинне бути прикладено деяке зусилля, яке за своєю величиною буде переважати певний потенціальний бар’єр. Так, наприклад, для виникнення так званої швидкої еластичної деформації необхідно прикласти таке зусилля, яке необхідне для орієнтації надмолекулярних утворень (пачок, сферолітів та перехідних областей). При цьому структурний елемент еластомерного матеріалу займає певне конформаційне положення, яке було енергетично невигідним у недеформованому стані. Швидкість розвитку даного типу деформації дорівнює швидкості звуку в матеріалі, який деформується. Для виникнення повільної еластичної деформації необхідним є розкручування пачок та окремих макромолекул. Оскільки в матеріалі всі структурні елементи пов’язані між собою, орієнтація проходить узгоджено. Цей тип деформації розвивається повільніше, для його виникнення потребується додаткова кількість енергії. Питома доля цих деформацій визначається здатністю структури до орієнтації і конформаційною рухливістю ланцюгів. Як швидка, так і повільна еластична деформації мають властивість оборотніх, тобто після зняття напруги зразок полімерного матеріалу повертається у вихідну форму. Енергія, яка була витрачена на деформування при цьому розсіюється у вигляді теплової внаслідок прийняття структурними елементами системи більш вигідного неорієнтованого (згорнутого) положення. Необоротною є так звана пластична деформація, що супроводжується руйнуванням окремих структурних елементів матеріалу або розриву міжмолекулярних зв’язків між ними. Доля пластичної деформації визначається здатністю структури до таких процесів, головним чином – енергією зв’язку між окремими елементами. Наприклад, у пластифікованих полімерів руйнуванню піддаються зв’язки між надмолекулярними утвореннями та низькомолекулярним пластифікатором або між молекулами низькомолекулярного пластифікатору. Ці зв’язки не потребують прикладення високої напруги та швидко рекомбінуються, таким чином надаючи матеріалу здатність легко текти під дією напруг. В той же час в крихких кристалічних полімерах для розвитку деформацій подібного типу необхідне руйнування зв’язків між макромолекулами та елементами надмолекулярної структури, що потребує набагато більше енергії ніж у випадку пластифікованих матеріалів. Ці три види деформації складають значення загальної граничної деформації матеріалу, яке дорівнює їх сумі. Вираз „загальна деформація” означає величину зміни лінійних розмірів зразку в момент його розриву по відношенню до початкової довжини цього зразку. Складові загальної деформації розвиваються в наступному порядку: швидка еластична, повільна еластична та пластична. В залежності від переважання кожної з них, матеріал може бути віднесеним до однієї з трьох груп: 1) високоеластичні матеріали (каучук, гуми); 2) еластичні матеріали (пластифікований ПВХ, силіконові гуми); 3) пластичні матеріали (напр. бітуми, фенолформальдегідні смоли новолачного типу). Для визначення долі деформацій окремого типу для початку визначають загальну деформацію за формулою (1). Далі встановлюють миттєву зміну розмірів (довжини) зразку після зняття напруги, що дозволяє визначити швидку еластичну деформацію (2). Наступний етап – встановлення величин повільної еластичної деформації за зміною розмірів зразку внаслідок релаксації (3). Пластичну деформацію визначають після проходження процесів релаксації напруг як відношення різниці кінцевої та початкової довжини зразка до початкової (4).
де εповн – загальна деформація зразку, l1 – довжина максимально деформованого зразку, l0 – початкова довжина зразку.
де εо – швидка еластична деформація зразку, l1 – довжина максимально деформованого зразку, l0 – початкова довжина зразку, l2 – довжина зразку через 1 сек після зняття навантаження.
де ε2 – повільна еластична деформація зразку, l3 – довжина зразку після 15 хвилин після зняття навантаження , l0 – початкова довжина зразку, l2 – довжина зразку через 1 сек після зняття навантаження.
де ε’ – пластична деформація зразку, l3 – довжина зразку після 15 хвилин після зняття навантаження , l0 – початкова довжина зразку.
Для визначення типу деформацій розраховують долю кожного окремого її виду по відношенню до загальної деформації.
Зразки: полімерні плівки (поліетилен низького тиску, поліетилен високого тиску, натуральний каучук, орієнтований лінійний поліетилен).
Прилади: лінійка, сушильна шафа, маркер для нанесення міток.
Хід роботи:
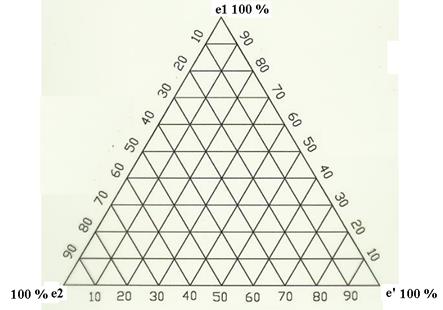
З плівок обережно вирізають зразки, які являють собою стрічки довжиною 10-12 см та шириною 1 см. По два зразки на один матеріал. Краї плівок повинні бути рівними, без порізів (в іншому випадку це призведе до передчасного руйнування зразку). На відстані 5-6 см посередині зразку проставляють мітки маркером. Плівки розтягують і фіксують максимальне видовження до розриву, що фіксується за допомогою лінійки за мітками. Розраховують значення загальної деформації (1). Далі плівку розтягують до 95 % від максимального видовження та відпускають, фіксуючи її розмір через 1 сек. після зняття напруги. Розраховують значення швидкої еластичної деформації (2). Зразок залишають в спокої на 15-20 хв. та спостерігають за змінами його довжини – після закінчення релаксаціїзнов заміряють відстань між мітками, фіксують її та розраховують повільну еластичну деформацію (3). Після цього визначають пластичну деформацію за формулою (4). Долі окремих деформації розраховуються шляхом прирівнювання загальної деформації до одиниці та знаходження долі кожної з деформацій від цієї одиниці за пропорцією. Одержані таким чином розрахункові дані використовують для побудови графічної ілюстрації розподілу деформацій за типами у вигляді трикутника Гіббса (Рис. 1).
Рис. 1. Трикутник Гіббса-Розенбома.
Правила побудови за трикутником наступні: сумарна доля трьох компонентів, які входять до діаграми повинна дорівнювати одиниці (або 100 %); кожен з кутів виражає стовідсоткову долю одного з компонентів; кожна зі сторін виражає такий стан, коли система є двохкомпонентною (третій компонент, кут якого протилежний до даної сторони – відсутній). Для побудови координати точки на сторонах трикутника відкладають вміст кожного з компонентів. Через ці точки паралельно до сторони, яка протилежна куту даного компоненту проводять лінію. Це повторюють для кожного з компонентів. В точці перетину ліній знаходяться координати системи.
Висновки: формулюються як результат роботи з: - Визначення долі деформацій зразків - Графічного порівняння розподілу деформацій матеріалів.
Контрольні запитання:
Поиск по сайту: |
 (1)
(1)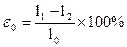 (2)
(2) (3)
(3)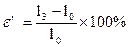 (4)
(4)