 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоретическое введение. Ознакомление с типовыми аттракторами диссипативных динамических систем
Ознакомление с типовыми аттракторами диссипативных динамических систем
Изучить процессы в диссипативных динамических системах на следующих моделях систем с типичными аттракторами:
- система с аттрактором типа «положение равновесия»: Параметры
- система с аттрактором типа «предельный цикл»:
Параметр
- система со «странным аттрактором»:
Параметры
Исследовать влияние параметров математических моделей и начальных условий на вид интегральных кривых и фазовых портретов.
Дополнительное задание 1: для системы странного аттрактора определить границы параметра r, при которых существует странный аттрактор, показать на примерах.
Исследование математической модели динамики конкурирующих видов. Теоретическое введение
Две популяции сходных биологических видов численностью
где параметры модели Уравнения модели получены на основе предположения, что прирост на одну особь Возможные процессы в моделируемой системе определяются свойствами ее положений равновесия, которым соответствуют нулевые значения скоростей изменения переменных системы. Для рассматриваемой модели возможны следующие исходы конкурентного взаимодействия видов: - оба вида сосуществуют; - вид 1 выживает, вид 2 вымирает; - вид 2 выживает, а вид 1 вымирает. Этим исходам соответствуют три положения равновесия, определяемые сочетанием параметров модели: 1. Условие выживания (сосуществования) обоих видов состоит в том, что положение равновесия должно иметь положительные координаты и быть асимптотически устойчивым. Координаты точки равновесия могут принимать положительные значения в следующих двух случаях: а) б) В первом случае положение равновесия будет устойчивым, оба вида будут сосуществовать, размер популяций при этом определяется координатами этой точки. Во втором случае положение равновесия, соответствующее сосуществованию видов, будет неустойчивым, а устойчивыми будут положения равновесия, соответствующие вымиранию одного из видов. При этом развитие процесса будет определяться начальными условиями.
Программа работы.
1. Построить компьютерную модель взаимодействия конкурирующих видов согласно заданной системе уравнений 2. Для значений параметров, заданных в таблице 1, рассчитать координаты точек равновесия. Таблица 1
3. Построить векторное поле в окрестности точек равновесия. 4. Провести моделирование процесса взаимодействия конкурирующих видов, приняв в качестве начальных условий координаты точки в окрестности положения равновесия. Провести моделирование при различных начальных условиях с целью выявления влияния начальных условий на характер переходного процесса. Здесь и далее моделирование проводить до достижения установившихся значений переменных состояния. 5. Изменить одно из значений параметров (для системы №1) таким образом, чтобы была достигнута следующая ситуация: а) вид 1 выживает, а вид 2 вымирает; б) вид 2 выживает, а вид 1 вымирает. Вычислить значения координат точек равновесия для обоих случаев. 6. Подобрать наборы параметров e, c, f, d для достижения всех трех ситуаций (сосуществование видов, вымирание первого вида, вымирание второго вида), если параметры а и b заданы следующим образом:
где N – номер варианта по списку. Дополнительное задание 2: для ситуации когда в системе более одной точки равновесия построить сепаратриссу.
Поиск по сайту: |





 Исследовать при
Исследовать при  =10.
=10. конкурируют друг с другом на некоторой территории с ограниченным запасом пищи. Модель конкуренции видов описывается следующей системой нелинейных дифференциальных уравнений:
конкурируют друг с другом на некоторой территории с ограниченным запасом пищи. Модель конкуренции видов описывается следующей системой нелинейных дифференциальных уравнений:
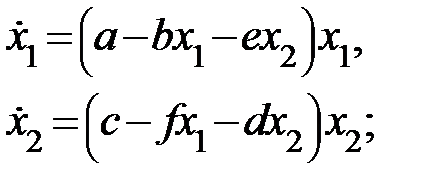
 > 0.
> 0. состоит из трех слагаемых: скорости размножения изолированной популяции
состоит из трех слагаемых: скорости размножения изолированной популяции 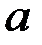 ; скорости уменьшения популяции в результате внутривидовой конкуренции
; скорости уменьшения популяции в результате внутривидовой конкуренции  ; скорости уменьшения популяции в результате межвидовой конкуренции
; скорости уменьшения популяции в результате межвидовой конкуренции  . Аналогично интерпретируются слагаемые второго уравнения.
. Аналогично интерпретируются слагаемые второго уравнения.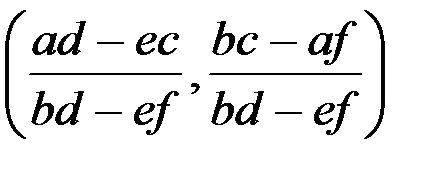 ; 2. (
; 2. (  ); 3.
); 3.  .
. ;
; .
. ,
,