 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Пусть
Знак минус возникает потому, что проекция силы противоположна направлению отклонения маятника. При малых отклонениях маятника от положения равновесия
Введем обозначение
Общим решением уравнения (3) можно считать функцию
Постоянные интегрирования А и
Из формулы (5) мы видим, что малые колебания маятника являются изохронными; их период не зависит от амплитуды и массы маятника. Именно это обстоятельство и позволяет использовать формулу (5) для определения ускорения силы тяжести. ФИЗИЧЕСКИЙ МАЯТНИК
Тело, совершающее колебания около неподвижной оси, не проходящей через его центр масс, называется физическим маятником. В данном случае тело совершает возвратно-вращательное движение. На рис.2 О след оси вращения на плоскости чертежа; ОО¢=
где
Для случая малых колебаний уравнение запишется в виде
где
Амплитуда колебаний
Здесь мы снова видим, что колебания маятника изохронны, таким образом, в принципе эти формулы можно использовать для определения ускорения силы тяжести.
Поиск по сайту: |
 Математическим маятником называют материальную точку, совершающую колебания на невесомой нерастяжимой нити. Естественно, что математический маятник – это физическая абстракция, физическая модель. Реальным образом ее может быть принят шарик малых размеров, подвешенный на достаточно длинной нити (рис.1).
Математическим маятником называют материальную точку, совершающую колебания на невесомой нерастяжимой нити. Естественно, что математический маятник – это физическая абстракция, физическая модель. Реальным образом ее может быть принят шарик малых размеров, подвешенный на достаточно длинной нити (рис.1). – длина нити маятника, т – его масса. Характеристиками, определяющими колебательное движение, можно считать или угол отклонения нити от равновесия
– длина нити маятника, т – его масса. Характеристиками, определяющими колебательное движение, можно считать или угол отклонения нити от равновесия  или же само отклонение х, отсчитываемое по траектории движения. Если пренебречь силами сопротивления движению, то на тело маятника действуют две силы: сила тяжести
или же само отклонение х, отсчитываемое по траектории движения. Если пренебречь силами сопротивления движению, то на тело маятника действуют две силы: сила тяжести  и натяжение нити
и натяжение нити  . В проекции на направление касательной
. В проекции на направление касательной  уравнение движения маятника запишется так:
уравнение движения маятника запишется так: (1)
(1)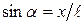 . Таким образом, уравнение движения (1) запишется в виде:
. Таким образом, уравнение движения (1) запишется в виде: . (2)
. (2) , имеем:
, имеем: . (3)
. (3) . (4)
. (4) определяются из начальных условий, тогда как циклическая частота колебательного движения маятника
определяются из начальных условий, тогда как циклическая частота колебательного движения маятника  . Вспомним, что период колебаний Т и их циклическая частота связаны соотношением
. Вспомним, что период колебаний Т и их циклическая частота связаны соотношением  . Откуда следует, что период колебаний математического маятника
. Откуда следует, что период колебаний математического маятника . (5)
. (5) Рис. 2
Рис. 2
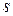 – расстояние от оси вращения до центра масс маятника. К телу приложены силы: тяжести
– расстояние от оси вращения до центра масс маятника. К телу приложены силы: тяжести  и реакции оси
и реакции оси  . Момент относительно оси вращения создает только сила
. Момент относительно оси вращения создает только сила  , (6)
, (6) – момент инерции тела относительно оси колебания;
– момент инерции тела относительно оси колебания;  – угловое ускорение тела;
– угловое ускорение тела;  , знак «–» имеет то же объяснение, что и в случае математического маятника. После соответствующих подстановок приходим к уравнению движения в виде:
, знак «–» имеет то же объяснение, что и в случае математического маятника. После соответствующих подстановок приходим к уравнению движения в виде: . (7)
. (7) , (8)
, (8)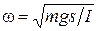 . Решением данного дифференциального уравнения будет функция
. Решением данного дифференциального уравнения будет функция . (9)
. (9) и начальная фаза определяются начальными условиями, а вот частота и период колебаний Т определяются параметрами физического маятника
и начальная фаза определяются начальными условиями, а вот частота и период колебаний Т определяются параметрами физического маятника ;
; 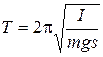 . (10)
. (10)