 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
I. Экспериментальное обоснование современных представлений о структуре атомов
Квантовые и волновые свойства вещества. Введение.
Все вещества состоят из атомов и молекул – известная фраза, которую можно найти в любом учебнике, ставшая афоризмом. Атом (от греческого atomos – неделимый) – наименьшая часть химического элемента, являющаяся носителем его свойств. Заслуга введения в теорию вещества идеи атомов принадлежит греческим философам (Демокрит, Эпикур). Нелегко понять, что подразумевали древние под термином «атом», но основной проблемой, интересовавшей их, был вопрос о том, бесконечна ли делимость вещества. Греческие атомисты верили, что любое вещество построено из «атомов» и, вероятно, чувствовали, что бесконечное многообразие свойств вещества должно быть объяснено конфигурацией и движением «атомов». Эти идеи довольно близки современным, но различия между нашими количественными теориями, основанными на опыте, и туманными размышлениями древних столь же огромны, как и отличие их «атомов» от того понимания, которое вкладываем в этот термин мы. Постепенно само существование атомов и молекул, которое долгое время рассматривалось только как удобная рабочая гипотеза, было осознано как объективная реальность. В начале XIX в. в результате установления основных химических законов и законов идеального газа сложились представления об атоме как о мельчайшей частице химического элемента (англ. Дж. Дальтон, итал. А. Авогадро, швед Я. Берцелиус). В середине XIX в. была проведена четкая граница между атомом и молекулой (итал. С. Канниццаро). Важнейшее значение имело открытие в 1869 г. Д.И. Менделеевым периодической системы элементов. Великие открытия конца XIX в. – рентгеновских лучей (1895 г.), радиоактивности (1896 г, франц. А. Беккерель), электрона (1897 г, англ. Дж. Дж. Томсон); результаты изучения радиоактивности (франц. П. и М.Кюри) окончательно разрушили представление о неизменности и неделимости атома. Стало очевидным, что атом имеет сложное строение.
I. Экспериментальное обоснование современных представлений о структуре атомов.
В 1903 г. Дж. Дж. Томсон предложил модель, согласно которой атом представляет собой положительно заряженную сферу (или равномерно заряженный шар), внутрь которой вкраплены электроны. Суммарный положительный заряд сферы равен заряду электронов, т.е. атом в целом нейтрален. Испускание света таким атомом – это следствие колебания электронов около положения равновесия. Первую попытку изучения строения атома на опытах по рассеянию пучков заряженных частиц предпринял Ленард с сотрудниками, используя катодные лучи – пучки электронов с энергией более Оказалось, что быстрые электроны почти совершенно не тормозятся атомом, хотя в результате столкновений с массивными шариками катодное излучение очень скоро неизбежно остановилось бы.
1.Опыт Резерфорда. Ядерная модель атома. В 1911 г. Э.Резерфорд поставил опыты по изучению рассеяния Узкий пучок
регистрировались визуально – удар экран (Э) из сернистого цинка, окружавший мишень, вызывал сцинтилляцию (вспышку света), наблюдаемую в микроскоп (М). Весь прибор помещался в вакуумированную оболочку.
Подавляющее число
Анализируя результаты опыта, Резерфорд пришел к выводу, что столь сильное отклонение вызывается чрезвычайно сильным электрическим полем, которое создается зарядом, связанным с большой массой и сконцентрированным в очень малом объеме. Остальное внутриатомное пространство практически ничем не заполнено – результат, уже полученный ранее Ленардом. Поскольку В отличие от Томсона, который отклонение на большие углы пытался объяснить множественными актами рассеяния, Резерфорд объяснил этот эффект однократным актом рассеяния и получил согласие с экспериментом. Исходя из кулоновского характера взаимодействия и известной скорости налетающих
Т.о., ядро обладает конечными размерами. Для почти центральных столкновений, т.е. рассеяния на большие углы, наблюдается отклонение распределения рассеянных частиц от формулы, полученной на основе закона Кулона. Отсюда следует вывод, что закон Кулона перестает быть справедливым на расстояниях около Т.о., согласно Резерфорду (1911 г.), атом можно представить себе следующим образом. В центре атома находится ядро с зарядом Проиллюстрировать масштабы и заполненность внутриатомного пространства можно на следующем примере. Если увеличить каплю воды до размеров земного шара и все атомы в ней в той же пропорции, то диаметр атома достигнет нескольких метров, а диаметр ядра составит лишь Замечания. 1. Планетарная модель была впервые предложена в лекции Перрена (J.Perrin) в Сорбонне в 1901 г.: положительно заряженная частица, окруженная некоторым числом электронов («наподобие маленьких планет»), компенсирующих заряд центральной частицы. Перрен предполагал, что под действием внутренних электромагнитных сил образуется динамически устойчивая система, периоды вращения в которой соответствуют частотам (длинам волн) линий спектра атома. 2. «Опыт Резерфорда» был поставлен Гейгером и Мёрсденом [H.Geiger, E.Mursden. On a diffuse reflection of the 3. В 1911 г. Резерфордом опубликована статья [The scattering of 4. Отклонение Резерфорду мы обязаны, прежде всего, нашими конкретными количественными представлениями о строении атома. Рассеяние частиц в атомной физике (физике элементарных частиц) принято описывать эффективным сечением. Эффективное сечение (
Т.о., следуя Резерфорду, получим выражение, связывающее эффективное сечение с углами рассеяния частиц. Определим эффективное сечение
Классическое решение задачи о рассеянии заряженной частицы на массивном точечном заряде было получено в механике (задача 2х тел), чем мы и воспользуемся.
Для
Поскольку в классике между параметрами Выразим дифференциал прицельного параметра
откуда
учитывая, что
Экспериментальная проверка полученной зависимости основана на следующих соображениях. Если акты рассеяния независимы, т.е. происходят на разных атомах,
Отсюда следует, что для заданного элемента телесного угла
что и было получено в эксперименте. Этот результат дал опытное обоснование модели атома Резерфорда. Однако эта модель противоречила представлениям классической физики: 1. Если заряды неподвижны, то такая система неустойчива (теорема Ирншоу). Поэтому Резерфорду пришлось отказаться от статической модели атома. 2. Если заряды движутся по искривленным орбитам, то тратится энергия на излучение при ускоренном движении и электроны должны в итоге упасть на ядро.
2.Спектры атомов.
Важный вклад в развитие представлений о структуре атомов внесли оптические исследования. Из опыта известно, что накаленные твердые тела имеют сплошные спектры излучения. У газов же, наряду со сплошными спектрами, наблюдались линейчатые и полосатые спектры. К 1900 г. было, в основном, выяснено, что полосатые спектры соответствуют излучению молекул, а линейчатые – атомов и ионов. Более того, оказалось, что в атомных спектрах линии располагаются не хаотически, а подчиняются некоторой закономерности. Наилучшим образом эти закономерности прослеживались в спектре атома водорода (и до некоторой степени у щелочных металлов), который измерил А.Ангстрем (1863 г.). В 1885 г. Бальмер установил аналитическую зависимость распределения излучения по длинам волн в спектре атома водорода.
или, переходя к частотам, (
где Если переписать выражение в виде
Здесь волны, укладывающихся в одном сантиметре. При изучении спектров излучения атомов было найдено, что спектральные линии могут быть объединены в группы, названные сериями. В пределах каждой серии положение линии подчиняется общей закономерности, которая носит название обобщенной формулы Бальмера .
Спектральные группы линий получили названия по именам исследователей:
………………………………………………………………………………… Наблюдаемые спектральные закономерности не укладывались в рамки классической теории, согласно которой параметры орбиты и угловая скорость движения по ней электрона могут принимать любые значения и как следствие обусловливать непрерывные спектры излучения атомов.
3.Боровская теория атома.
Выход из создавшегося тупика был найден Н.Бором в 1913 г., ценой введения предположений, противоречащих классическим представлениям.
Постулаты Бора. А) Существование стационарных состояний атома. Электроны движутся в атоме по определенным стационарным орбитам, которые удовлетворяют определенным квантовым условиям. Электрон, находясь на этих орбитах не излучает. Энергия атома может принимать только дискретные значения Б) Правило частот Бора. При переходе из одного стационарного состояния в другое атомы испускают или поглощают излучение строго определенной частоты:
Условие квантования. Для одномерного движения:
Круговая орбита – пример одномерного движения, при котором в качестве обобщенной координаты выступает угол, т.е.
который сохраняется, поскольку движение происходит в центральном поле. Тогда
Дополнив условие квантования основным уравнением динамики, описывающим движение электрона в электростатическом поле заряда ядра
т.о. радиусы боровских орбит могут принимать значения:
Для атома водорода (
Определим теперь энергию электрона в атоме. Полная энергия электрона складывается из кинетической энергии его движения по боровской орбите и потенциальной энергии взаимодействия с ядром атома.
учитывая (*), получаем
откуда находим энергию электрона на атома:
Спектр энергий электронов в атоме водорода определяется выражением (
Испускание и поглощение света, согласно боровской теории атома, определяется переходами электронов с одних энергетических уровней на другие, причем
 , (**) , (**)
где Т.о., частота испускаемого (поглощаемого) света, не связана с периодом (частотой) орбитального движения электрона, как это предполагалось ранее. Скорость орбитального движения электрона
Вычисленные по формуле (**) частоты спектральных линий водородного атома оказались в превосходном согласии с экспериментальными данными.
4.Опыты Д.Франка и Г.Герца . Существование дискретных энергетических уровней подтверждается опытами Д.Франка (1882-1964 гг.) и Г.Герца (1887-1975 гг.), осуществленными в 1914 г. Эти опыты были начаты с целью измерения потенциалов ионизации атомов ещё до формулировки постулатов Бора, но привели в итоге к их подтверждению. В эксперименте изучалось прохождение ускоренных электронов через пары ртути.
Экспериментальная установка представляла собой
под давлением Электроны, вылетавшие из катода вследствие термоэлектронной эмиссии, ускорялись в пространстве между катодом и сеткой разностью потенциалов, которую можно было плавно менять. Между сеткой и анодом создавалось задерживающее поле с постоянной разностью потенциалов около 0,5В. В эксперименте измерялась зависимость силы анодного
Ускоренные на промежутке катод-сетка электроны преодолевают задерживающую разность потенциалов и определяют величину анодного тока. Если бы в баллоне был вакуум, то вольт-амперная характеристика имела вид: Однако в опыте Франка и Герца сила тока сначала монотонно возрастала, достигая максимума при затем резко падала, и, пройдя через минимум, снова начинала расти. Максимумы тока повторялись при достижении на участке катод-сетка напряжения, кратного
исчерпывающее объяснение на основе боровской теории атома. На начальном участке соударения электронов с атомами ртути носят упругий характер, причем из-за большой разницы в массах энергия электрона при соударениях практически не изменяется. Т.о., при повышении ускоряющей разности потенциалов должна увеличиваться сила анодного тока, т.к. возрастает число электронов, способных преодолеть участок сетка-анод и внести вклад в анодный ток. При достижении разности потенциалов, соответствующей разности энергий между основным ( Если оставшаяся у электрона энергия недостаточна, чтобы преодолеть задерживающую разность потенциалов, он будет возвращаться на сетку, а на вольт-амперной характеристике будет наблюдаться участок спада анодного тока. При дальнейшем увеличении напряжения При достаточном разрежении паров ртути электроны на длине свободного пробега могут приобретать энергию, достаточную для перевода атома в следующее возбужденное состояние ( Время жизни атома в возбужденном состоянии порядка Теория Бора стала крупным шагом в развитии физики. Она отчетливо показала неприменимость классических подходов к внутриатомным процессам и значение квантовых законов в микромире. Однако после первых успехов теории все яснее давали себя знать её недочеты. Особенно тягостной неудача попыток построения теории атома гелия – одного из простейших атомов, непосредственно следующего за водородом. Слабость теории Бора заключалась в её логической противоречивости: она, опираясь на классическую механику, не была последовательно квантовой теорией и, поэтому, смогла стать только переходным этапом на пути к созданию теории атомных явлений.
Микрочастицами обычно называют элементарные частицы (электрон, протон, нейтрон и т.д.), также сложные частицы (ядра атомов, атомы, молекулы), образованные из сравнительно небольшого числа элементарных частиц.
1. Гипотеза де-Бройля.
В 1924 г. Луи де-Бройль (1892-1987гг.), пытаясь найти объяснение постулированным Бором условиям квантования атомных орбит, выдвинул смелую гипотезу, что дуализм не является исключительной особенностью оптических явлений, т.е. электромагнитных волн, а имеет универсальный характер. «В оптике,- писал он,- в течение столетия слишком пренебрегали корпускулярным способом рассмотрения по сравнению с волновым; не делалась ли в теории вещества обратная ошибка?». К этой гипотезе его привела, в частности, аналогия между геометрической оптикой и механикой Ньютона (ещё ранее замеченная Гамильтоном). Действительно, основные законы оптики и механики представляются в математически тождественной форме: движение частицы в поле с потенциалом Классическая механика приводит к наилучшим результатам тогда, когда частицу можно рассмотреть как материальную точку и приписать ей определенную траекторию движения. Аналогичная ситуация встречается в оптике, если длиной волны света можно пренебречь по сравнению с другими характерными длинами – это приближение геометрической оптики, когда волновые свойства не проявляются. Но геометрическая оптика способна описать далеко не все оптические явления, как и механика Ньютона - механические. Может быть, следует расширить аналогию и волновой оптике сопоставить волновую механику?! Идею волны, заимствованную из оптики, можно перенести в механику вполне последовательно. Однако прежде чем это сделать, следует подчеркнуть нетривиальность попытки объединения волновой и корпускулярной точек зрения. Действительно, энергия Итак, сначала попробуем развить теорию де-Бройля чисто формально.
СветЧастица (электромагнитная волна) (например, электрон)
Частота Волновой вектор
Переход к фотонам Переход к волнам (гипотеза де-Бройля)
Энергия Импульс Т.о., движению частицы массой
Распространение волн и движение свободных частиц можно описать уравнениями
2. Свойства волн де-Бройля.
1) Фазовая скорость.
Рассмотрим плоскую монохроматическую волну. Уравнение поверхности постоянной фазы
скоростью Аналогично, описывая движение частицы, можем найти фазовую скорость волны де-Бройля:
2) Групповая скорость. Групповая скорость (В разделе “Оптика” § Фазовая и групповая скорость определена из условия постоянства фазы амплитуды огибающей при сложении двух волн с близкими частотами). Из определения получаем Действительно, или Итак, групповая скорость волн де-Бройля равна скорости движения частицы. Интересно, что Полученный результат весьма привлекателен, в частности, велико искушение попытаться интерпретировать материальную частицу как волновой пакет, образованный в результате суперпозиции группы волн. И действительно, на основании соотношения а) Такого рода волновой пакет, вообще говоря, неустойчив и очень скоро расплывется, т.к. волны де-Бройля испытывают дисперсию в пустоте в силу зависимости фазовой скорости от длины волны, т.е. б) Частица-волна должна испытывать дифракцию. Поэтому с помощью дифракционной решетки можно разложить волновой пакет на составляющие, что снова приведет к уничтожению частицы.
3) Волны де-Бройля и стационарные орбиты.
3. Экспериментальное подтверждение гипотезы де-Бройля.
Ввиду смелости и необычности гипотезы де-Бройля о волновой природе вещества сразу же возникает естественный вопрос: можно ли и если да, то каким именно образом проверить эту гипотезу экспериментально? Понятно, что самое яркое свойство волн – возможность испытывать интерференцию и дифракцию, где наблюдаемой величиной, по сути, является длина волны. Такие опыты были проведены сначала с электронами, а затем с нейтронами и атомами. Сделаем некоторые оценки, позволяющие определить порядок длин волн с которым мы встретимся, имея дело с электронными пучками. Рассмотрим сначала нерелятивистский случай. Пусть электроны, ускоряемые электрическим полем, проходят разность потенциалов Примечание. Учитывать релятивистский характер движения электронов необходимо, начиная со значений ускоряющих напряжений
Де-бройлевские длины волн электрона для различных ускоряющих напряжений приведены в таблице.
1) Опыты Дэвиссона и Джермера.
В 1927 г. К.Дэвиссон (1881-1958 гг.) и Л.Джермер (1896-1971 гг.) [Davisson C.J., Germer L.H., Diffraction of Electrons by a Crystal of Nickel, Phys.Rev. 30, 705 (1927)] исследовали отражение электронов от монокристалла никеля. Опыты, приведшие к открытию дифракции электронов были начаты Дэвиссоном ещё в 1919 г. Однако первые результаты не увязывались с наличием волновых свойств у микрочастиц.
свойствами, рассеиваясь на подходящей решетке, должны дать дифракционную картину, первым обратил внимание Элзассер в 1925 г. Решетка кристалла “работает” аналогично дифракционной решетке: отраженные от кристаллических плоскостей волны материи образуют в результате суперпозиции дифракционную картину точно также, как вторичные волны от щелей дифракционной решетки. В своем историческом опыте Дэвиссон и Джермер использовали метод Брэгга: узкий пучок электронов, имеющих одинаковую скорость (моноэнергетических), направлялся на поверхность монокристалла никеля, обладающего кубической симметрией. Кристалл был сошлифован вдоль кристаллографической плоскости с миллеровскими индексами (111), т.е. перпендикулярно большой диагонали кристаллической ячейки.
Отраженные электроны улавливались цилиндрическим электродом, соединенным с гальванометром. Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. При нормальном к поверхности кристалла падении пучка максимум интенсивности наблюдался под углом
На диаграммах приведена зависимость интенсивности отраженного пучка от угла отражения Если кристалл рассматривать как совокупность параллельных атомных плоскостей, отстоящих друг от друга на расстоянии
(*) Так как Из последнего выражения видно, что дифракцию можно наблюдать двумя способами:
1.При постоянном ускоряющем напряжении 2.Проводить измерения при
Полученная при фиксированном угле скольжения Если на этом рисунке отложить вычисленные по формуле (**) значения
малых
В связи с этим Г.Бете предложил электронным волнам, как и электромагнитным, приписать показатель преломления:
фазовых скоростей В вакууме:
В металле:
где электрон, проникая в металл. Если ввести потенциалы, то можно записать
где электрона, прошедшего ускоряющую разность потенциалов Тогда
Отсюда получаем, что относительный показатель преломления среды равен
Разность хода интерферирующих лучей получаем
С учетом преломляющих свойств кристалла условие Брэгга-Вульфа принимает вид
Введение показателя преломления среды при описании распространения волн де-Бройля позволяет достичь полного согласия с экспериментом (в пределах точности эксперимента).
2) Опыты Томсона и Тартаковского.
В 1928 г. Дж.П.Томсон (1892-1975), а также П.С.Тартаковский (1895-1932) наблюдали дифракционную картину при прохождение электронов через тонкие пленки (фольгу, слюду), используя метод, предложенный Дебаем и Шерером для исследования поликристаллических материалов с помощью рентгеновских лучей.
пучок моноэнергетических электронов, ускоренных разностью потенциалов в несколько киловольт
направляется на исследуемый образец, толщина которого составляет образец, который равномерно вращается вокруг оси пучка, электроны рассеиваются на различные углы. Рассеянные электроны попадают на фотопластинку. Поликристаллический образец представляет собой совокупность хаотично ориентированных монокристаллов, среди множества которых найдутся такие, при отражении от которых для де-бройлевской волны выполняется условие Брэгга-Вульфа. Полученная таким образом электронограмма золота (рис.а) обнаруживает поразительное сходство с полученной в аналогичных условиях рентгенограммой алюминия (рис.б).
Т.о., эксперименты показали, что прохождение электронов сквозь тонкие пленки сопровождается появлением характерной дифракционной картины точно такого же вида, что и рентгеновские интерференционные кольца Дебая-Шерера. Зная диаметр кольца и расстояние до экрана, можно найти постоянную кристаллической решетки
2) Дифракция атомов и молекул. В 1930 г. Штерн с сотрудниками установил, что отражение легких атомов и молекул (
молекул по скоростям устранялся с помощью селектора скоростей - двух зубчатых колес, насаженных на одну ось – выделялись близкие по скорости молекулы. В качестве индикатора использовался чувствительный манометр.
Положение боковых максимумов относительно центрального меняется с температурой, т.к. изменяется де-бройлевская длина волны молекулы газа. Открытие Штерна было очень важным и впечатляющим. Правильность соотношения де-Бройля для молекулярных пучков была подтверждена с точностью 1%. А ведь здесь мы имеем дело уже с материальными частицами, из которых состоят, как известно, не только газы, но также и жидкости и твердые тела. Если перехватить пучок, уже претерпевший дифракцию на кристаллической решетке, и направить в сосуд, то мы обнаружим все тот же газ с самыми обычными свойствами.
4) Дифракция нейтронов.
Убедиться в волновой природе вещества можно также, изучая рассеяние нейтронов на решетках кристаллов. Для тепловых нейтронов (нейтронов, энергия которых соответствует температуре
Поиск по сайту: |
 .
. частиц при прохождении через тонкие металлические фольги. Резерфорд выбрал для своих экспериментов значительно более массивные
частиц при прохождении через тонкие металлические фольги. Резерфорд выбрал для своих экспериментов значительно более массивные  .
. из тонкой фольги. Рассеянные
из тонкой фольги. Рассеянные  -частиц рассеивалось на малые углы
-частиц рассеивалось на малые углы  , однако некоторое количество
, однако некоторое количество ). Например, на платиновой фольге из
). Например, на платиновой фольге из 
 падающих
падающих  (одна) рассеивалась на угол больше
(одна) рассеивалась на угол больше  .
. , где
, где  заряд
заряд  заряд ядра. Траектории
заряд ядра. Траектории 
 , пусть
, пусть  (серебро),
(серебро),  ,
,  .
. (или, иначе, выполняется на расстояниях, больших
(или, иначе, выполняется на расстояниях, больших  , имеющее размер, не более
, имеющее размер, не более  . Вокруг ядра распределены
. Вокруг ядра распределены  электронов, в области размером порядка
электронов, в области размером порядка  . Масса атома сосредоточена, в основном, в ядре.
. Масса атома сосредоточена, в основном, в ядре. .
. particles by matter and structure of the atom,- Phyl.Mag., v.21,1911], содержавшая формулу рассеяния и обоснование планетарной (ядерной) модели атома.
particles by matter and structure of the atom,- Phyl.Mag., v.21,1911], содержавшая формулу рассеяния и обоснование планетарной (ядерной) модели атома. ,
,  . Резерфорд же, объясняя этот результат однократным актом рассеяния, получил в согласии с экспериментом
. Резерфорд же, объясняя этот результат однократным актом рассеяния, получил в согласии с экспериментом  . Кроме того, как выяснилось позже, модель Томсона не объясняет эффекта Штарка, не допускает эффекта Зеемана и т.д.
. Кроме того, как выяснилось позже, модель Томсона не объясняет эффекта Штарка, не допускает эффекта Зеемана и т.д. ) – величина, характеризующая вероятность перехода системы двух сталкивающихся частиц в результате их рассеяния (упругого или неупругого) в определенное конечное состояние. Упругое рассеяние частиц характеризуют дифференциальным эффективным сечением
) – величина, характеризующая вероятность перехода системы двух сталкивающихся частиц в результате их рассеяния (упругого или неупругого) в определенное конечное состояние. Упругое рассеяние частиц характеризуют дифференциальным эффективным сечением  , равным отношению числа частиц, упруго рассеянных в единицу времени в единичный телесный угол (
, равным отношению числа частиц, упруго рассеянных в единицу времени в единичный телесный угол (  элемент телесного угла), к потоку падающих частиц; а также полным эффективным сечением , равным интегралу дифференциального сечения, взятому по полному телесному углу
элемент телесного угла), к потоку падающих частиц; а также полным эффективным сечением , равным интегралу дифференциального сечения, взятому по полному телесному углу  стерадиан. Эффективное сечение всецело определяется видом рассеивающего поля и является важнейшей характеристикой процесса рассеяния; имеет размерность площади.
стерадиан. Эффективное сечение всецело определяется видом рассеивающего поля и является важнейшей характеристикой процесса рассеяния; имеет размерность площади. как отношение числа
как отношение числа  частиц, рассеиваемых в единицу времени на углы от
частиц, рассеиваемых в единицу времени на углы от  до
до  , к плотности потока
, к плотности потока 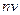 (интенсивности
(интенсивности  ) рассеиваемых частиц, т.е. к числу частиц, проходящих в единицу времени через единичную площадку, перпендикулярную их скорости
) рассеиваемых частиц, т.е. к числу частиц, проходящих в единицу времени через единичную площадку, перпендикулярную их скорости 
 (
(  - концентрация частиц в пучке):
- концентрация частиц в пучке): .
. .
. ) связь между прицельным параметром
) связь между прицельным параметром  (длина перпендикуляра, опущенного из рассеивающего центра, на направление касательной к траектории находившейся на бесконечности частицы) и углом рассеяния:
(длина перпендикуляра, опущенного из рассеивающего центра, на направление касательной к траектории находившейся на бесконечности частицы) и углом рассеяния: , или
, или  . (*)
. (*) (в телесный угол
(в телесный угол  ), определяется числом частиц, прошедших через площадку
), определяется числом частиц, прошедших через площадку  , т.е.
, т.е. , продифференцировав выражение (*):
, продифференцировав выражение (*):

 ,
, ,
, , получаем для дифференциального сечения рассеяния:
, получаем для дифференциального сечения рассеяния:
 – формула Резерфорда.
– формула Резерфорда. число атомов-рассеивателей в единице объема мишени,
число атомов-рассеивателей в единице объема мишени,  объем, в котором происходит рассеяние, то число
объем, в котором происходит рассеяние, то число  , можно найти, используя формулу Резерфорда
, можно найти, используя формулу Резерфорда .
. должно выполняться условие
должно выполняться условие ,
,
 ,
, )
) ,
, - постоянная Ридберга (1890 г.),
- постоянная Ридберга (1890 г.),  ,
,  - целое число:
- целое число:  3, 4, 5,…
3, 4, 5,… , то
, то  .
. в согласии с принятой в спектроскопии традицией обозначает волновое число, т.е. число длин
в согласии с принятой в спектроскопии традицией обозначает волновое число, т.е. число длин , где
, где 

 - серия Лаймана (1916 г.) – ультрафиолетовые лучи;
- серия Лаймана (1916 г.) – ультрафиолетовые лучи;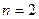 - серия Бальмера (1885 г.) – видимый свет;
- серия Бальмера (1885 г.) – видимый свет; - серия Пашена (1908 г., предсказал Ритц) – инфракрасные лучи;
- серия Пашена (1908 г., предсказал Ритц) – инфракрасные лучи; - серия Брэккета (1922 г.) – инфракрасные лучи;
- серия Брэккета (1922 г.) – инфракрасные лучи; - серия Пфунда (1924 г.) – инфракрасные лучи;
- серия Пфунда (1924 г.) – инфракрасные лучи;
 .
. ,
,  2, 3,…
2, 3,… - обобщенный импульс;
- обобщенный импульс;  обобщенная координата.
обобщенная координата. а роль обобщенного импульса играет момент количества движения
а роль обобщенного импульса играет момент количества движения ,
, или
или  .
. :
:

 (*),
(*),
 ) первая боровская орбита (
) первая боровская орбита (  – боровский радиус.
– боровский радиус.
 ,
, ,
, боровской орбите
боровской орбите ,
,  1, 2, 3,…
1, 2, 3,… .
. .
.

 - постоянная Ридберга и
- постоянная Ридберга и  .
. трехэлектродную лампу, заполненную парами ртути
трехэлектродную лампу, заполненную парами ртути мм.рт.ст.
мм.рт.ст. тока от напряжения между катодом и сеткой.
тока от напряжения между катодом и сеткой. ,
, и т.д.
и т.д. Такое поведение зависимости
Такое поведение зависимости  получает
получает ) и первым возбужденным (
) и первым возбужденным (  ) состояниями атома, появляется возможность неупругого столкновения электрона с атомом, сопровождающегося передачей последнему порции энергии
) состояниями атома, появляется возможность неупругого столкновения электрона с атомом, сопровождающегося передачей последнему порции энергии  .
. электроны, претерпевшие неупругое соударение, смогут достичь анода. Нарастание анодного тока будет происходить до тех пор, пока напряжение на участке катод-сетка не достигнет значения удвоенного первого потенциала возбуждения атома, и т.д.
электроны, претерпевшие неупругое соударение, смогут достичь анода. Нарастание анодного тока будет происходить до тех пор, пока напряжение на участке катод-сетка не достигнет значения удвоенного первого потенциала возбуждения атома, и т.д. ). В этом случае на кривой
). В этом случае на кривой  ).
). , после чего он возвращается в основное состояние, испуская фотон с частотой
, после чего он возвращается в основное состояние, испуская фотон с частотой  .
.
 можно рассматривать так же, как движение светового луча в среде с соответствующим показателем преломления
можно рассматривать так же, как движение светового луча в среде с соответствующим показателем преломления 
 частицы относятся к точечной, т.е. обладающей пренебрежимо малыми размерами, массе. Напротив, частота
частицы относятся к точечной, т.е. обладающей пренебрежимо малыми размерами, массе. Напротив, частота  и волновой вектор
и волновой вектор  характеризуют бесконечно протяженную во времени и пространстве волну. Трудно представить себе более далекие и несовместимые друг с другом идеи, чем эти две концепции, которые квантовая теория должна объединить в одно целое.
характеризуют бесконечно протяженную во времени и пространстве волну. Трудно представить себе более далекие и несовместимые друг с другом идеи, чем эти две концепции, которые квантовая теория должна объединить в одно целое.


 Частота
Частота 
 Длина волны
Длина волны 
 , где
, где  . Это волна де-Бройля.
. Это волна де-Бройля.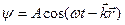


 . Эта плоскость перемещается вдоль направления волнового вектора
. Эта плоскость перемещается вдоль направления волнового вектора  . Фазовая скорость электромагнитной волны в вакууме
. Фазовая скорость электромагнитной волны в вакууме  . Для волн, распространяющихся в среде,
. Для волн, распространяющихся в среде,  .
. , где
, где  , – фазовая скорость волны де-Бройля больше скорости света. Следовательно, фаза волны материи распространяется со скоростью, превосходящей скорость света. Однако в этом нет большой беды. Полученный результат свидетельствует лишь о том, что фазовая скорость не может характеризовать движение физического объекта или передачу информации и в этом смысле лишена определенного физического содержания. Действительно, фазовая скорость есть чисто искусственное понятие, т.к. её нельзя измерить на опыте. Для измерения фазовой скорости необходимо как-нибудь «пометить» определенную часть бесконечной и плавно изменяющейся волны и затем проследить, с какой скоростью будет перемещаться «метка». Единственный способ сделать такую «метку» состоит в том, чтобы в результате интерференции на ранее гладкой волновой поверхности возник какой-либо горб, например, при сложении двух волн с близкими частотами. Таким образом, приходится измерять не фазовую скорость исходной волны, а скорость движения созданного горба. Последняя называется групповой скоростью.
, – фазовая скорость волны де-Бройля больше скорости света. Следовательно, фаза волны материи распространяется со скоростью, превосходящей скорость света. Однако в этом нет большой беды. Полученный результат свидетельствует лишь о том, что фазовая скорость не может характеризовать движение физического объекта или передачу информации и в этом смысле лишена определенного физического содержания. Действительно, фазовая скорость есть чисто искусственное понятие, т.к. её нельзя измерить на опыте. Для измерения фазовой скорости необходимо как-нибудь «пометить» определенную часть бесконечной и плавно изменяющейся волны и затем проследить, с какой скоростью будет перемещаться «метка». Единственный способ сделать такую «метку» состоит в том, чтобы в результате интерференции на ранее гладкой волновой поверхности возник какой-либо горб, например, при сложении двух волн с близкими частотами. Таким образом, приходится измерять не фазовую скорость исходной волны, а скорость движения созданного горба. Последняя называется групповой скоростью. – измеряемая величина.
– измеряемая величина. – скорость движения частицы.
– скорость движения частицы. ,
, .
. .
. в течение некоторого времени частицу было принято считать образованием группы волн де-Бройля. Т.е. полагали, что волны первичны, а частицы представляют собой их образования – волновые пакеты. Однако оказалось, что все не так просто. Эта весьма заманчивая интерпретация наталкивается на непреодолимые трудности.
в течение некоторого времени частицу было принято считать образованием группы волн де-Бройля. Т.е. полагали, что волны первичны, а частицы представляют собой их образования – волновые пакеты. Однако оказалось, что все не так просто. Эта весьма заманчивая интерпретация наталкивается на непреодолимые трудности. . В то же время мы знаем, что частицы живут весьма долго.
. В то же время мы знаем, что частицы живут весьма долго. Согласно постулатам Бора условие квантования круговых орбит:
Согласно постулатам Бора условие квантования круговых орбит:  . Отсюда получаем
. Отсюда получаем  , т.е.
, т.е.  . Это означает, что на круговой орбите укладывается целое число волн де-Бройля. Таким образом, имеется красивая интерпретация стационарных состояний – стоячая волна де-Бройля, которая, как известно, энергию не переносит (не излучает).
. Это означает, что на круговой орбите укладывается целое число волн де-Бройля. Таким образом, имеется красивая интерпретация стационарных состояний – стоячая волна де-Бройля, которая, как известно, энергию не переносит (не излучает). . Тогда скорость электрона находим из условия
. Тогда скорость электрона находим из условия  , а его импульс:
, а его импульс:  . Длина волны де-Бройля такого электрона равна
. Длина волны де-Бройля такого электрона равна  , если длина волны измеряется в ангстремах, а напряжение – в вольтах. Оценки показывают, что при ускоряющих напряжениях от единиц вольт до киловольт де-бройлевская длина волны электрона приблизительно такая же, как у мягкого рентгеновского излучения. При
, если длина волны измеряется в ангстремах, а напряжение – в вольтах. Оценки показывают, что при ускоряющих напряжениях от единиц вольт до киловольт де-бройлевская длина волны электрона приблизительно такая же, как у мягкого рентгеновского излучения. При  длина волны электрона
длина волны электрона  соответствует уже жесткому рентгену. Т.о., для наблюдения дифракции электронов, как и в случае рентгеновских лучей, можно использовать решетку кристалла.
соответствует уже жесткому рентгену. Т.о., для наблюдения дифракции электронов, как и в случае рентгеновских лучей, можно использовать решетку кристалла. .
. ;
;
 .
.
 1 10 102 103 4.104 105 106
1 10 102 103 4.104 105 106 12,25 3,9 1,22 0,39 0,061 0,039 0,012
12,25 3,9 1,22 0,39 0,061 0,039 0,012 0,059 0,037 0,008
0,059 0,037 0,008 На то, что электроны, обладающие подобно пучкам света волновыми
На то, что электроны, обладающие подобно пучкам света волновыми

 , наиболее значительный при
, наиболее значительный при  .
.
 для различных значений ускоряющего напряжения. Вертикальная ось определяет направление падающего пучка. Сила тока в гальванометре пропорциональна длине отрезка, проведенного из начала координат до пересечения с кривой.
для различных значений ускоряющего напряжения. Вертикальная ось определяет направление падающего пучка. Сила тока в гальванометре пропорциональна длине отрезка, проведенного из начала координат до пересечения с кривой. , то дифракцию можно рассматривать как результат отражения пучка от системы таких плоскостей. Положение максимумов интенсивности (дифракционных максимумов) определяется условием Брэгга-Вульфа:
, то дифракцию можно рассматривать как результат отражения пучка от системы таких плоскостей. Положение максимумов интенсивности (дифракционных максимумов) определяется условием Брэгга-Вульфа: , где
, где  угол скольжения;
угол скольжения;  , то, подставляя в (*), получаем
, то, подставляя в (*), получаем  ,
, 
 .
. ) изменять угол
) изменять угол  , поворачивая либо кристалл, либо коллектор.
, поворачивая либо кристалл, либо коллектор. , изменяя разность потенциалов и, следовательно, де-бройлевскую длину волны электрона.
, изменяя разность потенциалов и, следовательно, де-бройлевскую длину волны электрона. отклонение рассчетных значений от эмпирических при
отклонение рассчетных значений от эмпирических при ).
). , или через отношение
, или через отношение
 .
. ,
, (в нерелятивистском приближении
(в нерелятивистском приближении 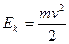 ).
).
 ,
, - глубина потенциальной ямы, в которую попадает
- глубина потенциальной ямы, в которую попадает ,
, внутренний потенциал металла, а кинетическая энергия
внутренний потенциал металла, а кинетическая энергия .
. .
. ,
,  .
. из рассмотрения простой геометрической задачи.
из рассмотрения простой геометрической задачи. ;
;  ;
; ;
;  ;
; .
.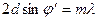 , или окончательно
, или окончательно .
. Суть эксперимента состоит в следующем. Узкий
Суть эксперимента состоит в следующем. Узкий
 ,
, . Проходя через
. Проходя через

 .
. ) от поверхности кристалла также сопровождается дифракционными явлениями. Выбор химических элементов был обусловлен длиной де-бройлевской волны, которая, например, для гелия при комнатной температуре составляет
) от поверхности кристалла также сопровождается дифракционными явлениями. Выбор химических элементов был обусловлен длиной де-бройлевской волны, которая, например, для гелия при комнатной температуре составляет  , т.е. порядка постоянной
, т.е. порядка постоянной кристаллической решетки. Тепловой разброс
кристаллической решетки. Тепловой разброс
 ) длина волны де-Бройля равна
) длина волны де-Бройля равна  . Тепловые нейтроны используются в методе Лауэ. Пучок направляется на неподвижный монокристалл, а затем отраженные кристаллическими плоскостями нейтроны в направлениях, определяемых условием Брэгга-Вульфа, образуют, так называемые, пятна Лауэ. Дифракционная картина, возникающая в результате рассеяния нейтронов, дает богатую информацию о кристаллической структуре твердых тел.
. Тепловые нейтроны используются в методе Лауэ. Пучок направляется на неподвижный монокристалл, а затем отраженные кристаллическими плоскостями нейтроны в направлениях, определяемых условием Брэгга-Вульфа, образуют, так называемые, пятна Лауэ. Дифракционная картина, возникающая в результате рассеяния нейтронов, дает богатую информацию о кристаллической структуре твердых тел.