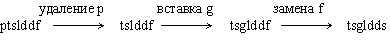|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Переформулировка задачи 11
Рекуррентные соотношения и динамическое программирование
Задача 1. Вычислить значение суммы S = 1/1! + 1/2! + ... + 1/k!
[Решение] Избавиться от вычисления факториала для каждого слагаемого. Задача 2. Написать программу определения количества шестизначных 'счастливых' билетов, у которых сумма первых 3 десятичных цифр равна сумме 3 последних десятичных цифр.
[Решение] Самое простое - это перебрать все возможные комбинации шести цифр и подсчитать число "счастливых" билетов. Count:=0; {количество "счастливых" билетов}for a1:=0 to 9 dofor a2:=0 to 9 dofor a3:=0 to 9 dofor a4:=0 to 9 dofor a5:=0 to 9 dofor a6:=0 to 9 doif a1+a2+a3=a4+a5+a6then Count:=Count+1;Условие if во вложенных циклах будет проверяться 106 раз, поэтому будем говорить, что сложность этого алгоритма 106. 2) Обратим внимание на то, что в "счастливом" билете последняя цифра a6 однозначно определяется первыми пятью: a6=(a1+a2+a3)-(a4+a5). Если 0<=a6<=9, то билет "счастливый", иначе - нет. Таким образом, мы можем убрать шестой вложенный цикл: Count:=0;for a1:=0 to 9 dofor a2:=0 to 9 dofor a3:=0 to 9 dofor a4:=0 to 9 dofor a5:=0 to 9 dobegina6:=(a1+a2+a3)-(a4+a5);if (a6>=0) and (a6<=9)then Count:=Count+1;end;Сложность алгоритма 105. 3) Если комбинаций a1 a2 a3 первых трех цифр с суммой T=a1+a2+a3 насчитывается C[T], то всего "счастливых" билетов с суммой половины T=a1+a2+a3=a4+a5+a6 будет C[T]*C[T]. Всех возможных сумм T-28 (от 0=0+0+0 до 27=9+9+9). Подсчитаем C[i], i=0, ..., 28, затем найдем интересующее нас количество "счастливых" билетов C[0]2 + C[1]2 + ... + C[27]2. Заметим, что "счастливых" билетов с суммой T столько же, сколько и с суммой 27-T. Действительно, если билет a1 a2 a3 a4 a5 a6 с суммой T - "счастливый", то таковым же является и билет (999999 - a1 a2 a3 a4 a5 a6) с суммой 27-T. Поэтому число билетов можно вычислять и по формуле 2*(C[0]2+ ... +C[13]2), т.е.рассматривать только суммы T от 0 до 13.
Задача 3. Написать программу определения количества 2*N -значных билетов, у которых сумма первых N десятичных цифр равна сумме N последних десятичных цифр; при этом N -произвольное натуральное число.
[Решение] Задача имеет очевидное решение, которое состоит в генерации всех 2*n-разрядных чисел и проверке их на требуемое свойство. Однако общее количество таких чисел равно 102n и поэтому при n>3 практически очень трудно получить результат на ЭВМ. Следовательно необходимо разработать алгоритм, не требующий генерации чисел. Определим через S(k,i) количество k-разрядных чисел, сумма цифр которых равна i. Например, S(2,3)=4, так как существует 4 двуразрядных числа (03,12,21,30), сумма цифр которых равна 3. Легко заметить, что S(1,i)=1 при i<10 и S(1,i)=0 при i>9. Предположим теперь, что мы сумели вычислить значения величин S(n,i) для всех i от 0 до 9*n, т.е. мы знаем, сколько существует n-разрядных чисел с суммой цифр, равной 0,1,...,9*n (максимальное число цифр в n-разрядном числе). Тогда нетрудно убедиться, что общее количество 'счастливых' 2*n-разрядных чисел равно P=S(n,0)*S(n,0)+S(n,1)*S(n,1)+...+S(n,9*n)*S(n,9*n). Действительно, каждое 'счастливое' 2*n-разрядное число может быть получено склейкой двух произвольных n-разрядных чисел с одинаковой суммой цифр. Таким образом, необходимо уметь вычислять значения величин S(k,i) для всех k<=n,i<=9*k. Определим способ вычисления S(k+1,i) через значения величин S(k,j), j<=i. Понятно, что любое k+1-разрядное число может быть получено из k-разрядного добавлением еще одного разряда (цифры). Следовательно S(k+1,i) = S(k,i-ц1)+S(k,i-ц2)+..., где ц1,ц2,... - возможные добавленные цифры. Ясно, что это 0,1,...,m где m=min(9,i). Следовательно, S(k+1,i) = S(k,i-0)+S(k,i-1)+...+ S(k,i-m).
Задача 4. Фишка может двигаться по полю длины N только вперед. Длина хода фишки не более K. Найти число различных путей, по которым фишка может пройти поле от начала до конца. Пример. N=3, K=2 Возможные пути: 1,1,1 1,2 2,1 Ответ: 3.
[Решение] Очевидное решение задачи предполагает разложение числа N на всевозможные суммы таким образом, чтобы каждое слагаемое в сумме не превосходило k. Очевидно, что таких разложений очень много, особенно если учитывать, порядок слагаемых в разложении существенен, так как он соответствует различной последовательности ходов фишки. Обозначим через S(i) количество различных путей, по которым фишка может пройти поле от начала до позиции с номером i. Предположим теперь, что для любого j от 1 до i известны значения величин S(j). Задача состоит в определении правила вычисления значения S(i+1), используя значения известных величин. Легко заметить, что в позицию с номером i+1 фишка может попасть из позиций i, i-1,...,i-k. Следовательно, S(i+1)=S(i)+S(i-1)+...+S(i-k). Таким образом, вычисляя последовательно значения величин S(1), S(2),..., S(N) по описанному выше правилу, получаем значение S(N), которое и указывает общее количество различных путей, по которым фишка может пройти поле от начала до позиции с номером N.
Задача 5. Покупатель имеет купюры достоинством A(1), ...,A(n), а продавец - B(1), .. ,B(m). Необходимо найти максимальную стоимость товара Р, которую покупатель не может купить, потому что нет возможности точно рассчитаться за этот товар с продавцом, хотя денег на покупку этого товара достаточно.
[Решение] Если покупатель отдаст все свои купюры продавцу, то понятно, что для решения исходной задачи размер минимальной сдачи, которую продавец не может вернуть, используя любые имеющиеся теперь у него купюры C[i] (его и покупателя). Для этого удобно отсортировать купюры согласно их достоинства в порядке неубывания. Предположим, что продавец может вернуть любую сдачу от 1 до S, используя только меньшие i купюр. Для следующей (i+1)-ой купюры достоинства C[i+1] возможны 2 ситуации. 1. C[i+1]<S+2. Тогда понятно, что продавец может вернуть любую сдачу от 1 до C[i+1]+S, т.к. любая из этих сумм представима либо первыми i купюрами, либо (i+1)-ой купюрой вместе с некоторыми из первых i купюр. 2. C[i+1]>S+1. Тогда понятно, что продавец не может вернуть сдачу S+1. Опишем процедуру вычисления S.
Задача 6. Задан массив М [1:N] натуральных чисел, упорядоченный по неубыванию, т.е.: M[1]<=M[2]<=...<=M[N]. Найти первое натуральное число, не представимое суммой никаких элементов этого массива, при этом сумма может состоять и из одного слагаемого, но каждый элемент массива может входить в нее только один раз.
[Решение] Решается аналогично задаче 5. Задача 7. У покупателя есть n монет достоинством H(1),..., H(n). У продавца есть m монет достоинством B(1),...,B(l). Может ли купить покупатель вещь стоимости S так, чтобы у продавца нашлась точная сдача (если она необходима).
[Решение] Если S>H(1)+...+H(n), то сумму выплатить нельзя. Если покупатель отдаст все свои купюры продавцу, то понятно, что для решения исходной задачи надо определить, может ли продавец вернуть сумму H(1)+...+H(n)+B(1)+...+B(l)-S, используя любые имеющиеся теперь у него купюры M[i] (его и покупателя). Для этого удобно отсортировать купюры согласно их достоинства в порядке неубывания. Пусть P=M[1]+M[2]+ ... +M[n+l]. Решим чуть более общую задачу: найдем все непредставимые данными купюрами суммы на промежутке от 0 до P. Заведем массив A[0 .. P] натуральных чисел. Элемент A[i]=1, если мы можем выплатить сумму i (т.е. существует набор купюр суммарного достоинства i), и A[i]=0 иначе. Будем строить всевозможные суммы, используя последовательно 0,1,2,...,N купюр. Очевидно, что сумма из ноля купюр - это ноль, поэтому сначала A[0]=1. Предположим, что мы нашли всевозможные суммы, которые можно составить, используя не более (k-1) - ой купюры M[1], ..., M[K-1]. Добавим еще одну купюру M[k]. Теперь мы можем выплатить следующие суммы: 1) Все суммы, которые можно было составить с помощью купюр M[1], ... , M[K-1]. 2) Все суммы, которые можно было составить с помощью купюр M[1], ... , M[K-1], увеличенные на M[K]. Расстановка новых пометок в массиве A может выглядеть следующим образом: for i:=P-M[K] downto 0 do if A[i]=1 then A[i+M[K]]:=1; Мы проходим по массиву справа налево для того, чтобы не использовать повторно впервые образованную на данном шаге сумму. После выполнения n+l шагов алгоритм заканчивает работу. Если известно, что H(1)+...+H(n)+B(1)+...+B(l)-S не превосходит некоторой константы D, то тогда массив A имеет смысл брать не из P, а из D элементов.
Задача 8. Задан массив М [1:N] натуральных чисел, упорядоченный по неубыванию, т.е.: M[1]<=M[2]<=...<=M[N]. Написать алгоритм выплаты заданной суммы S минимальным количеством купюp достоинством M(1), ..., M(N).
[Решение] Решается аналогично задаче 7. При этом достаточно завести массивы var A, KOL, PredSum, B: array [0..P] of byte; Назначение массива A - как и в предыдущей задаче. Массив В служит для временного хранения предыдущих сумм. Элементы KOL[i] и PredSum[i] указывают соответственно минимальное количество элементов, участвующих в получении суммы со значением i и предыдущую сумму, из которой была получена добавлением одного слагаемого сумма i. Формирование этих массивов осуществляется параллельно с заполнением массива А. Сначала A[0]=1, A[i]=0 для всех i>0,KOL[0]=0, KOL[i]=254, для всех i>0, (считаем, что если KOL[i]=254, то сумму i набрать нельзя),PredSum[i]=0 для всех i>0;for i:=1 to N do {цикл по всем купюрам}beginfor j:=M[i] to P {цикл по всем возможным суммам с участием купюры M[i]}if (A[j-M[i]]<>0) and{если можно набрать сумму j-M[i]}(KOL[j]>KOL[j-M[i]]+1) {и добавлением купюры M[i] мы получаем сумму j из меньшего количества купюр}then beginKOL[j]:=KOL[j-M[i]]+1 {то запоминаем это новое количество и в B[j] заносим новую}B[j]:=j-M[i];{информацию о предыдущей сумме}A[j]:=1;{и помечаем, что сумму j набрать можно} endelse B[i]:=PredSum[j]; {иначе дублируем старую информацию} for j:=M[i] to P do {Дублируем информацию из B} PredSum[j]:=B[j]; {в PredSum}end;Почему мы не можем непосредственно записывать новую информацию о предыдущей сумме в массив PredSum? Обратите внимание, что массивы A и KOL дублируют друг друга. Напишите тот же фрагмент программы, объединив функции массивов A и KOL в одном массиве A. После завершения работы предыдущего фрагмента если A[S]=1, то сумму S набрать можно с помощью KOL[S] купюр. Предыдущая сумма (до добавления последней купюры) была S'= PredSum[S], следовательно последняя купюра есть S-PredSum[S]. Аналогично выписываем купюры, требуемые для представления суммы S' (используя PredSum[S']). Задача 9. По матрице A(N,N) построить матрицу B(N,N). Элемент B(I,J) равен максимальному из элементов матрицы А принадлежащем части, ограниченной справа диагоналями, проходящими через A(I,J).
[Решение] Очевидное решение задачи состоит в использовании некоторой процедуры, которая по заданным координатам (номеру строки i и номеру столбца j) элемента определяет максимальное значение элементов, расположенных в нужной части матрицы A. Однако нетрудно заметить, что для элементов первого столбца матрицы В справедливо соотношение B[i,1]=A[i,1], i=1,...N. Вычисление же других столбцов можно проводить следующим образом: B[i,j]=max(A[i,j], B[i-1,j-1], B[i,j-1], B[i+1,j-1]). При этом необходимо учитывать, что индексы элементов должны находится в пределах границ массива.
Задача 10. Вводится матрица a(m,n) из 0 и 1. Найти в ней квадратную подматрицу из одних единиц максимального размера.
[Решение] В элемент a[i,j] матрицы будем заносить длину максимальной стороны квадрата из единиц, у которого элемент (i,j) есть верхний левый угол (очевидно, что если a[i,j]=0, то квадрат построить нельзя). Матрицу A будем просматривать по строкам справа налево, снизу вверх. Предположим, что текущий просматриваемый элемент a[i,j] (все элементы, лежащие в строках с номерами больше i, равно как и все элементы строки i правее a[i,j] считаются уже к этому моменту просмотренными). Если элемент a[i,j]=0, то его значение остается нулевым. Если же a[i,j]=1, то для того, чтобы найти максимальный размер квадрата из единиц, у которого (i,j) - верхний левый угол, проанализируем уже просмотренные элементы a[i,j+1], a[i+1,j+1], a[i+1,j] - соответственно длины сторон максимальных квадратов с левым углом справа, по диагонали вниз и просто вниз от данного элемента. Квадрат с верхним левым углом (i,j) может протянуться вправо на больше чем на a[i+1,j]+1, вниз - не больше чем на a[i,j+1]+1 и по диагонали не больше чем на a[i+1,j+1]+1. Следовательно, максимальная сторона квадрата есть a[i,j]=min{a[i,j+1],a[i+1,j],a[i+1,j+1]}+1.
Задача 11. Вводится матрица a(m,n) из 0 и 1. Найти в ней прямоугольную подматрицу из одних единиц максимального размера (т.е. с максимальным произведением высоты на длину).
[Решение] Пусть верхний левый угол матрицы имеет индекс (1,1). Будем для каждой строки i формировать вектор p[1..M] такой, что p[j] есть число последовательных единичных элементов в столбце j, начиная с элемента (i,j) и выше его. Таким образом, если p[j]=0, то A[i,j]=0, а если p[j]=u>0, то A[i,j]=A[i,j+1]= ... =A[i,j-u+1]=1, а элемент A[i,j-u] нулевой (если, конечно, такой элемент есть в матрице, т.е. если j-u>0). Тогда площадь (сумма элементов) единичного прямоугольника S_i(L,R) с нижними правым и левым углами в элементах (i,R) и (i,L) соответственно есть площадь основания (R-L+1) умноженная на высоту этого прямоугольника h(L,R)=минимальное p[i] по всем j, изменяющимся от L до R. Для каждой строки i надо найти максимум величины S_i(L,R) при 1<=L<=R<=M, а максимум по всем строкам и даст искомую величину. Очевидно, что для первой строки p[j]=A[1,j]. Если мы знаем вектор l для строки i, то мы можем вычислить его для строки (i+1) по следующей формуле if A[i+1,j]=0 then p[j]:=0 Более коротко это же можно записать и так: p[j]:=(p[j]+1)*A[i+1,j]; Будем рассматривать вектор p, соответствующий строке i, и для каждого индекса j, 1<=j<=M, определим максимальный размер единичного прямоугольника с высотой p(j), располагающегося в столбцах с номерами от L(j) до R(j), L(j)<=j<=R(j), нижняя граница которого строка i. Очевидно, что L(j) есть увеличенный на единицу индекс первого меньшего чем p[j] элемента вектора p при просмотре p от j-го элемента влево, или L(j)=1, если такого меньшего элемента нет. Аналогично, R(j) есть уменьшенный на 1 индекс первого меньшего чем p[j] элемента вектора p при просмотре p от j-го элемента вправо, или R(j)=M, если такого элемента нет. Как быстро вычислить L(j) и R(j)? Используя алгоритм 8 Главы "Структуры данных" мы можем найти все L и R за два прохода по вектору p: Будем заполнять массив R. Вектор p просматриваем слева направо. Организуем стек для позиций элементов. Для каждого текущего p[j] будем выталкивать из стека все позиции, на которых стоят элементы большие текущего, и заносить в соответствующие этим позициям места массива R число (j-1). Замет позицию текущего элемента j поместить в стек. После просмотра всех элементов в стеке будут стоять индексы позиций массива R, в которые необходимо занести число M. var Stack: array [0..M] of byte;...S[0]:=0; {стек пуст, S[0] есть указатель на последнююпомещенную в стек позицию}for j:=1 to M dobeginwhile p[j]<p[S[S[0]]] do{S[0] - это индекс последней занятой позиции в стеке, на которой находится число S[S[0]] - индекс элемента массива p, а сам этот элемент - это p[S[S[0]]]}beginR[S[S[0]]]:=j-1; {для элемента массива p с индексом S[S[0]] нашли координату правой стенки}S[0]:=S[0]-1;{убрать элемент из стека}end;S[0]:=S[0]+1;{индекс - в стек}S[S[0]]:=j;end;for j:=1 to S[0] do R[S[S[0]]]:=M;Для заполнения массива L необходимо проделать те же самые операции, но вектор p будет просматриваться справа налево: ... S[0]:=0; {стек пуст, S[0] есть указатель на последнююпомещенную в стек позицию}for j:=M downto 1 dobeginwhile p[j]<p[S[S[0]]] dobeginL[S[S[0]]]:=j+1; {для элемента массива p с индексом S[S[0]] нашли координату левой стенки}S[0]:=S[0]-1;{убрать элемент из стека}end;S[0]:=S[0]+1;{индекс - в стек}S[S[0]]:=j;end;for j:=1 to S[0] do L[S[S[0]]]:=1;Последнее, что остается сделать - это за один проход вычислить максимум по всем j выражения p[j]*(R[j]-L[j]+1). Этот максимум есть размер максимального единичного прямоугольника с нижней гранью в строке i. Максимум по всем i и даст решение. Сложность алгоритма O(N*M), т.е. количество операции линейно зависит от числа элементов матрицы A!
Переформулировка задачи 11. Фермер хочет построить на своей земле как можно больший по площади сарай. Но на его участке есть деревья и хозяйственные постройки, которые он не хочет никуда переносить. Для простоты представим ферму сеткой размера MxN. Каждое из деревьев и построек размещается в одном или нескольких узлах сетки. Прямоугольный сарай не должен ни с чем соприкасаться (т.е. в соседних с ним узлах сетки не может ничего быть). Найти максимально возможную площадь сарая и где он может размещаться. Задача 12. Дан массив A[N,M]. Необходимо найти максимальную сумму элементов прямоугольного подмассива по всем возможным прямоугольным подмассивам.
[Решение] Пусть элемент C[i,j] массива C есть следующая сумма C[i,j]=A[1,j]+ ... +A[i,j]. Переменная MaxSoFar имеет то же самое назначение, что и раньше,MaxFndingHere есть максимальное значение суммы элементов прямоугольной подматрицы с правым нижним углом (i,j) и высоты k.
Задача 13. Задана матрица натуральных чисел A(n,m). За каждый проход через клетку (i,j) взымается штраф A(i,j). Необходимо минимизировать штраф и а) Пройти из какой-либо клетки 1-ой строки в n-ую строчку, при этом из текущей клетки можно перейти 1) в любую из 3-х соседних, стоящих в стpоке с номеpом на 1-цу большем; 2) в любую из 8 соседних клеток; б) Реализовать пункт a) для перехода из клетки (1,1) в (n,m).
[Решение]
Задача 14. Дан выпуклый n-угольник, n=>3, своим обходом по контуру. Разбить его на треугольники (n-3)-мя диагоналями, непересекающимися кроме как по концам, таким образом чтобы а) Cумма их длин была минимальной; б) Максимальная из диагоналей имела наименьшую длину.
[Решение] Задача 15. Задано число А и два вектора b[1..n] и c[1..n]. Найти множество I, являющееся подмножеством множества {1,...,n}, такое, что
возможных
[Решение] Задача 16. Пусть x=(a1,a2,...,am) и y=(b1,b2,...,bn) - две заданных строки символов. Определим d(x,y) как минимальное число вставок, удалений и замен символа, которое необходимо для преобразования x в y. Например: d(ptslddf,tsgldds)=3
Для заданных x и y найти d(x,y).
[Решение] Задача 17. Вводится три неотрицательных числа d, i, c и две строки X и Y. Найти преобразование строки X в Y минимальной стоимости. Допустимы следующие три операции: удалить любой символ из X (стоимость операции d); вставить любой символ в X (стоимость операции i); заменить символ в X на произвольный (стоимость операции e).
[Решение] Задача 18. Даны две строки x и y. Строка x состоит из нулей и единиц, строка y из символов A и B. Можно ли строку x преобразовать в строку y по следующему правилу: цифра 0 преобразуется в непустую последовательность букв A, а цифра 1 - либо в непустую последовательность букв A, либо в непустую последовательность букв B?
[Решение] Задача 19. Пусть известно, что для перемножения матрицы размера n*m на матрицу размера m*k требуется n*m*k операций. Необходимо определить, какое минимальное число операций потребуется для перемножения n матриц А1,...Аn, заданных своими размерами n(i)*m(i). При этом можно перемножать любые две рядом стоящие матрицы, в результате чего получается матрица нужного размера. Замечание: n(i) - число строк в матрице Ai m(i) - число столбцов в матрице Ai n(i)=m(i)+1.
[Решение] Задача 20. а) Из последовательности, состоящей из N чисел, вычеркнуть минимальное количество элементов так, чтобы оставшиеся образовали строго возрастающую последовательность. б) Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, одной пары соседних элементов ( одного "разрыва" возрастающей подпоследовательности). Например: A=(1,2,3,2,4,3,4,6); Искомая подпоследовательность (1,2,3,2,3,4,6) Разрыв подчеркнут. --- б) Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, m пар соседних элементов ( возрастающая подпоследовательность с m "разрывами").
[Решение] Задача 21. В заданной последовательности целых чисел найти максимально длинную подпоследовательность чисел такую, что каждый последующий элемент подпоследовательности делился нацело на предыдущий.
[Решение] Задача 22. Возвести число А в натуральную степень n за как можно меньшее количество умножений.
[Решение] Задача 23. Заданы z и y - две последовательности. Можно ли получить последовательность z вычеркиванием элементов из y.
[Решение] Задача 24. Найти максимальную по длине последовательность z, полученную вычеркиванием элементов как из x, так и из y.
[Решение] Задача 25. Пусть x и y - две бинарных последовательности (т.е. элементы последовательностей - нули и единицы); x и y можно рассматривать как запись в двоичной форме некоторых двух натуральных чисел. Найти максимальное число z, двоичную запись которого можно получить вычеркиванием цифр как из x, так и из y. Ответ выдать в виде бинарной последовательности.
Поиск по сайту: |



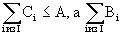 является максимальной из всех
является максимальной из всех