 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Динамика вращательного движения относительно
Момент инерции. Теорема Штейнера Примеры решения задач 8.1.Найти моменты инерции системы относительно осей 0 х и 0у, состоящей из 4-х шариков массами: m1 = m, m2 = 2∙m, m3 =3∙m, m4 = 4∙m и, расположенных в вершинах прямоугольника со сторонами a и b = 2∙a.
следовательно
Ответ: 28∙m∙a2; 5∙m∙a2. 8.2.Вычислить момент инерции тонкого однородного стержня относительно оси перпендикулярной его середины (См. рис.).
где тогда
т.к. Ответ: 8.3. Вычислить момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, то R2 можно вынести из под знака интеграла
где Ответ: 8.4. Вычислитьмомент инерции однородного диска относительно оси, перпендикулярной его плоскости и проходящей через центр.
Площадь поверхности обруча равна произведению его длины на толщину: 2× p× s× ds . Поскольку масса т диска распределена равномерно, то масса обруча dm пропорциональна площади его поверхности Момент инерции обруча был найден в задаче 8.3.
Осталось просуммировать моменты инерции всех таких обручей Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси. Ответ: 8.5.Вычислить момент инерции шара относительно его диаметра.
Радиус такого диска равен
  . .
Объём диска dVz равен произведению его площади на толщину
Плотность материала шара равна
Тогда масса диска
Момент инерции диска был найден в задаче 8.4. В применении к данному случаю, он равен
Момент инерции шара находится интегрированием по всем таким дискам
Ответ: 8.6.Найти момент инерции однородного цилиндра массой m и радиусом R относительно оси 0¢0¢, параллельной оси симметрии цилиндра 00 и, отстоящей от неё на расстоянии d = 1,5∙R.
тогда
Ответ:
Динамика вращательного движения относительно Неподвижной оси Примеры решения задач 9.1. Зависимость угла поворота однородного диска массой 10 кг и радиусом 1 м от времени задаётся уравнением
уравнение: Подставим приведённые выражения в уравнение
Произведём вычисления
Ответ: 20 Н. 9.2. Материальная точка массой m = 0,1 кг вращается равноускоренно по окружности радиусом R = 0.2 м. За 75полных оборота из состояния покоя она достигает частоты вращения n = 15 об/с. Найти время движения точки, момент силы, действующий на неё, и момент импульса для этого времени.
С учётом соотношений (1) - (4), имеем
Зависимость угловой скорости от времени при равноускоренном движении
После подстановки (1), (2), (5) в (6), найдём время движения точки,
Основной закон динамики вращательного движения относительно неподвижной оси
Т.к. момент инерции точки
Момент импульса материальной точки при вращении по окружности
Произведём вычисления
Ответ:10 с; 0,038 Н× м; 0,38 кг× м2/с. 9.3. Простейшая машина Атвуда (См. рис., с. 82), применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами m1и m2,которые подвешены на легкой нити, перекинутой через неподвижный блок массой m3. Считая нить невесомой и нерастяжимой и, пренебрегая трением в оси блока, определить ускорение грузов.
По третьему закону Ньютона
Запишем второй закон Ньютона для грузов m1и m2
Спроецируем эти уравнения на ось 0y
Вычтем из первого уравнения второе и с учётом (1), получим Запишем основной закон динамики вращательного движения блока относительно неподвижной оси
Выпишем в явном виде все величины, входящие в уравнение: Подставим указанные выражения в уравнение динамики (4) с учётом (2) Формулу (5) подставим в уравнение (3)
откуда
Ответ: 9.4.Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением e = 0,4 рад/с2. Определить кинетическую энергию маховика в момент времени t2 = 25 c, если в момент времени t1 = 10 с момент импульса маховика составлял L1 = 60 кг× м2/с.
Решение. Момент импульса маховика
Кинетическая энергия вращательного движения маховика
Угловая скорость
Тогда
Следовательно
Произведём вычисления
Ответ: 750 Дж. 9.5.Однородный цилиндр радиусом R = 0,1 м и массой m = 1 кг скатывается по наклонной плоскости длиной ℓ = 2 м и углом к горизонту a = 300 (См. рис., с. 84). Найти время движения цилиндра по наклонной плоскости.
Решение. Цилиндр участвует в двух движениях: поступательном и вращательном. Поступательное движение подчиняется второму закону Ньютона
Проецируем на ось 0x
Вращательное движение подчиняется основному уравнению динамики вращательного движения относительно оси
где Тогда
Подставим (2) в (1)
откуда
Запишем уравнение кинематики поступательного движения
Следовательно
С учётом (3)
После подстановки числовых значений
Ответ: 1,1 с.
t = 20 с, если масса колеса равномерно распределена по ободу и равна m = 10 кг, а диаметр колеса равен d = 20 см? Коэффициент трения между колодкой и ободом колеса равен m = 0,5.
Решение. Угловое ускорение при равнопеременном вращении
Момент инерции колеса
Момент касательной силы
Сила трения
Тогда
Запишем основное уравнение динамики вращательного движения
или с учетом (1), (2), (3)
Произведём вычисления
Ответ:18,85 Н.
Поиск по сайту: |
 Решение.
Каждый шарик можно считать материальной точкой, т. е.
I = m
Решение.
Каждый шарик можно считать материальной точкой, т. е.
I = m  ,
где r – расстояние от точки до оси (См. рис.).
Момент инерции – величина аддитивная, т. е.
,
где r – расстояние от точки до оси (См. рис.).
Момент инерции – величина аддитивная, т. е.
 ,
,
 .
.
 ,
, – масса элемента стержня длиной
– масса элемента стержня длиной  , т.е.
, т.е.  .
. ,
, .
. .
.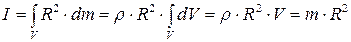 ,
,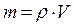 — полная масса обруча.
— полная масса обруча. .
.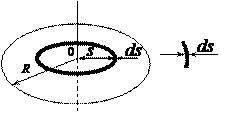 величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьём диск на бесконечно тонкие обручи радиусом s и толщиной ds (См.рис.).
величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьём диск на бесконечно тонкие обручи радиусом s и толщиной ds (См.рис.). .
. .
. .
. .
. от центра (См.рис.).
от центра (См.рис.). .
. .
. .
. .
.
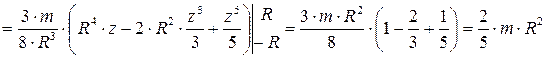 .
. .
. ,
,
 ,
,  ,
,
 .
. .
. (рад), где С = 2 рад/с2. Найти величину касательной силы.
(рад), где С = 2 рад/с2. Найти величину касательной силы. .
Выпишем в явном виде все величины, входящие в
.
Выпишем в явном виде все величины, входящие в
 - момент инерции диска;
- момент инерции диска;  - угловое ускорение;
- угловое ускорение;  - момент силы.
- момент силы. .
. (Н).
(Н). .
.  Запишем формулы для угла поворота
Запишем формулы для угла поворота
 .
. 
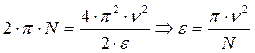 . (5)
. (5) (c). (6)
(c). (6) .
.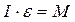 .
.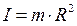 и, с учётом (5),
и, с учётом (5), .
. .
. .
. . (1)
. (1) . (2)
. (2) .
.
 .
.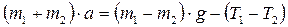 .(3)
.(3) . (4)
. (4) - момент инерции диска;
- момент инерции диска;  - угловое ускорение;
- угловое ускорение;  - момент вращающей силы.
- момент вращающей силы.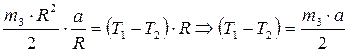 . (5)
. (5) ,
, .
. .
. .
.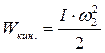 .
. .
. .
. .
. (Дж).
(Дж).
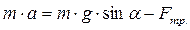 (1)
(1) .
. . (2)
. (2) ,
, . (3)
. (3) Рис. к задаче 9.5.
Рис. к задаче 9.5.
 .
. .
. .
. (с).
(с). 9.6.С какой силой по модулю P следует прижать тормозную колодку к ободу колеса (См. рис.), делающего n0 = 30 об/с, для его остановки в течение
9.6.С какой силой по модулю P следует прижать тормозную колодку к ободу колеса (См. рис.), делающего n0 = 30 об/с, для его остановки в течение . (1)
. (1) . (2)
. (2) .
. .
. . (3)
. (3) ,
, .
. (H).
(H).