 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Геометрическая интерпретация первообразной
Пусть функция
Рис. 1.2.
Рассмотрим криволинейную трапецию Найдём производную функции
Если
Итак,
Среди первообразных В частности, площадь
Пример 1.4. Вычислить площадь
Рис.1.3. Решение. Первообразная функции Используя формулу (1.3), получим
Отсюда следует, что площадь параболического сегмента
Замечание 1.2. В связи с тем, что между вычислением интегралов и вычислением площадей плоских фигур – квадратурой – существует связь, вычисление интегралов тоже принято называть квадратурой.
1.8. Простейшее дифференциальное уравнение. Задача Коши
Одна из задач интегрального исчисления – задача нахождения первообразной данной функции. Обозначим данную функцию через
Если
График решения дифференциального уравнения называют интегральной кривой.Если Пусть точка Эту задачу называют задачей Коши, или начальной задачей. Числа Итак,
В силу следствия 1.3 решение задачи Коши единственно. Решить задачу Коши – значит среди бесконечного множества интегральных кривых выделить интегральную кривую, проходящую через точку
Пример 1.5. Решим задачу Коши:
Решение. Здесь
Поиск по сайту: |
 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  .
.
 , изображённую на рис. 1.2. Определим на отрезке
, изображённую на рис. 1.2. Определим на отрезке  следующим образом: каждому значению
следующим образом: каждому значению  поставим в соответствие величину
поставим в соответствие величину  , заключённой между начальной ординатой
, заключённой между начальной ординатой  и ординатой, отвечающей значению
и ординатой, отвечающей значению 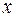 .
. :
: 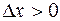 ,
,  . В силу непрерывности функция
. В силу непрерывности функция  достигает на отрезке
достигает на отрезке  своих наименьшего
своих наименьшего  и наибольшего
и наибольшего 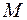 значений. Очевидно, площадь
значений. Очевидно, площадь  заключена между площадями прямоугольников, построенных на основании
заключена между площадями прямоугольников, построенных на основании  , откуда
, откуда  .
. значения
значения  и
и  будут изменяться и в силу непрерывности функции
будут изменяться и в силу непрерывности функции 
 Поэтому
Поэтому .
.
 функции
функции  в точке
в точке  . Поэтому
. Поэтому 
 криволинейной трапеции
криволинейной трапеции 

 есть функция
есть функция 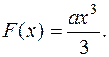

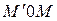 равна
равна  т.е. двум третям площади описанного прямоугольника
т.е. двум третям площади описанного прямоугольника  .
. . Тогда задача нахождения первообразной может быть записана в виде уравнения:
. Тогда задача нахождения первообразной может быть записана в виде уравнения:

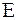 функция, то уравнение
функция, то уравнение  .
. некоторая интегральная кривая, то все остальные могут быть получены из неё простым сдвигом вдоль оси
некоторая интегральная кривая, то все остальные могут быть получены из неё простым сдвигом вдоль оси 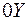 на произвольный отрезок
на произвольный отрезок  .
. ,
, 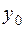 - произвольное число. Поставим задачу: найти решение уравнения
- произвольное число. Поставим задачу: найти решение уравнения 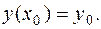
 называют начальными значениями величин
называют начальными значениями величин  ; условие
; условие  - начальным условием.
- начальным условием.

 .
. .
. . Очевидно, что
. Очевидно, что  Решение задачи Коши состоит в том, чтобы среди бесконечного множества интегральных кривых
Решение задачи Коши состоит в том, чтобы среди бесконечного множества интегральных кривых  найти кривую, проходящую через точку
найти кривую, проходящую через точку  . Подставим в равенство
. Подставим в равенство  начальные данные:
начальные данные:  Получим равенство:
Получим равенство:  . Отсюда следует, что
. Отсюда следует, что  Итак,
Итак,  – искомое решение (решение задачи Коши).
– искомое решение (решение задачи Коши).