 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Точечная и пространственная симметрияСтр 1 из 7Следующая ⇒
СТРУКТУРА КРИСТАЛЛИЧЕСКИХ И АМОРФНЫХ ТЕЛ
Структурными единицами вещества являются атомы, молекулы или ионы. Из агрегатных состояний вещества конденсированными являются два – жидкое и твердое. Твердые тела подразделяют по взаимному расположению атомов на кристаллические и аморфные, различие между которыми заключается в степени упорядоченности частиц в пространстве. В аморфных веществах наблюдается ближний порядок, когда взаимно упорядочены ближайшие атомы, но эта упорядоченность периодически не повторяется на больших расстояниях. Кристаллические вещества характеризуются дальним порядком, при котором взаимная упорядоченность ближайших соседей периодически повторяется в пространстве. Вводятся понятия точечной и пространственной симметрии, решеток Браве, кристаллографических индексов, зон Бриллюэна. Рассматривается связь физических свойств кристалла и его симметрии. Приведены примеры анизотропии и полиморфизма. Даны краткие сведения о жидких кристаллах, полимерах, аморфных телах и керамиках.
Структура кристаллов
Главными макроскопическими признаками кристаллического состояния является однородность, анизотропия и симметрия. Однородность кристаллического состояния означает, что в произвольных областях кристалла его свойства являются тождественными. Макроскопическая однородность предусматривает, что размеры кристалла должны быть такими, чтобы не сказывалась дискретность атомного строения. То есть для линейных L, плоскостных S и объемных V размеров образца должны выполняться условия:
где а – расстояние между соседними атомами в кристалле (~ 0,1 нм). Однородность можно определить как инвариантность физических свойств
Таким образом, кристалл можно рассматривать как непрерывную, однородную среду без учета дискретности его строения. Такой подход лежит в основе феноменологического описания физических свойств и широко применяется в физике. Условие макроскопической однородности является характерным не только для кристаллического состояния, но и для аморфных и стекловидных материалов, жидкостей и газов. Особенность кристаллов по сравнению с аморфными материалами заключается в их анизотропии. Анизотропия – это зависимость физических свойств вещества (механических, оптических, электрических, магнитных и др.) от направления. Анизотропия свойственна также жидким кристаллам и полимерам. Анизотропия определяется атомным строением и не обязательно связана с отличием свойств по разным направлениям. Для некоторых различных направлений свойства могут быть одинаковыми, что является проявлением симметрии кристалла. Симметрия кристалла – это свойство кристалла совмещаться самим с собой при поворотах, отражениях, параллельных переносах. Симметрия внешней формы кристалла определяется симметрией его атомного строения. Она же определяет и симметрию физических свойств кристалла. Для описания внутренней организации (структуры) кристалла удобно использовать понятие пространственной или кристаллической решетки (рис.1.1).
Кристаллическая решетка - это пространственная сетка, в узлах и некоторых других характерных точках которой расположены частицы (атомы или молекулы), которые образуют твердое тело. Рассматривая геометрию решетки, стоит отвлечься от теплового движения частиц и рассматривать неподвижную решетку, определяющую положение центров, относительно которых происходят колебания. Решетку можно характеризовать тройкой векторов Параллелепипед, построенный на основных трансляциях решетки, называется элементарной ячейкой. Длины ребер (периоды) а, b, c и углы a, b, g между ними однозначно характеризуют элементарную ячейку (рис. 1.2).
Элементарная ячейка должна удовлетворять двум условиям: иметь минимальный объем и при размножении векторами трансляции покрывать все пространство кристалла.
Точечная и пространственная симметрия
В физике твердого тела важную роль играет понятие геометрической симметрии. Симметрия означает возможность преобразования объекта, которое совмещает его с собой. Под симметрией кристаллов понимают свойство кристаллов совмещаться с собой после выполнения некоторых симметричных операций. В общем значении симметрия – неизменность (инвариантность) объектов и законов при некоторых преобразованиях описывающих их переменных. Теория симметрии кристаллов – это теория симметричных преобразований самого в себя трехмерного пространства с учетом того, что внутренняя атомная структура кристаллов трехмерная периодическая, то есть описывается как кристаллическая решетка. Для кристаллов конечных размеров возможны такие операции симметрии как поворот кристалла на определенный угол и отображение в плоскости, для кристаллов бесконечных размеров следует прибавить еще трансляцию (параллельный перенос). Операции симметрии – это отражения, вращения, переносы (трансляции), которые приводят пространство (фигуру) в совмещение с самим собой. Для описания структуры конкретного кристалла необходимо: – определить кристаллическую решетку; – выбрать кристаллографическую систему координат; – найти базис; – определить набор преобразований симметрии, которая совмещает кристаллическую структуру саму с собой. Элементы операций симметрии создают множество (конечное или бесконечное), которое называется группой симметрии. Множество элементов называется группой, если для этих элементов выполняются следующие условия: 1. На множестве элементов 2. На множестве элементов 3. На множестве элементов 4. Выполняется закон ассоциативности Бесконечный набор векторов трансляции, при переносе на которые кристалл совмещается сам с собой, образует трансляционную группу. Кристаллические структуры имеют два типа симметричных преобразований: точечная симметрия и пространственная симметрия. Точечной группой симметрии называют совокупность точечных операций симметрии, которые совмещают решетку саму с собой. Общее число независимых точечных групп симметрии кристаллов составляет 32. Эти группы включают конечное количество элементов. Трансляционная симметрия отображает то обстоятельство, что одинаковые атомы в одинаковом окружении повторяются в разных точках кристалла и любую из этих точек можно перевести в положение, которое совпадает с другой точкой, с помощью операции трансляции. Совокупность элементов точечной и трансляционной групп симметрии образуют пространственную группу симметрии. Общее количество независимых пространственных групп симметрии кристаллов 230. Операции точечной симметрии оставляют неподвижной одну точку пространства. Представим список элементов точечной симметрии: – плоскость симметрии (плоскость зеркальной симметрии); – центр симметрии (центр инверсии); – ось симметрии определенного порядка; – инверсионные оси симметрии. Плоскостью симметрии m (англ. mirror – зеркало) называется воображаемая плоскость, которая делит фигуру на две зеркально равные части. Центром симметрии (инверсии) является особая точка, операция инверсии относительно которой приводит к идентичному взаимному расположению точек. Операция инверсии перемещает точку с координатами Осью симметрии порядка Операция зеркальной симметрии сводится к отображению в некоторой плоскости (зеркале), которую называют плоскостью симметрии. Последовательно могут выполняться не только однотипные, но и разнотипные симметричные преобразования. Например, комбинация поворота вокруг оси и зеркальное отражение в плоскости, перпендикулярной к этой оси, приводит к появлению новых элементов симметрии – зеркально поворотных осей В кристаллах на элементы симметрии налагаются определенные ограничения. Можно доказать, что в кристаллах существуют только оси симметрии Оси пятого, седьмого и высших порядков в кристаллах невозможны, но они характерны для так называемых квазикристаллов и биологических объектов. Сочетания последовательных вращений вокруг разных осей всегда связаны в группы из трех. Это случается потому, что поворот вокруг любой оси, например А, на угол В кристаллографии используется несколько способов обозначения элементов симметрии. Самыми распространенными являются международные обозначения, в которых поворотные оси отражаются цифрами 1, 2, 3, 4, 6; инверсионные – Подобными международной символике являются обозначения Шубникова, в которых вместо зеркально инверсионных используются зеркально поворотные оси В физике твердого тела используются также обозначения Шенфлиса[2]:
Индексами
Поиск по сайту: |
 . (1.1)
. (1.1)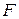 кристалла относительно произвольного переноса начала координат
кристалла относительно произвольного переноса начала координат  :
: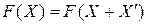 , (1.2)
, (1.2)
 и
и  , которые называются основными трансляциями решетки. Эти векторы не лежат в одной плоскости и подбираются таким образом, чтобы вектор T=n1a+n2b+n3c совпадал со всеми узлами решетки, когда
, которые называются основными трансляциями решетки. Эти векторы не лежат в одной плоскости и подбираются таким образом, чтобы вектор T=n1a+n2b+n3c совпадал со всеми узлами решетки, когда  и
и  принимают любые положительные и отрицательные значения. Выбор векторов а, b, и c, вообще говоря, неоднозначный.
принимают любые положительные и отрицательные значения. Выбор векторов а, b, и c, вообще говоря, неоднозначный.
 задан закон умножения элементов, то есть если элементы
задан закон умножения элементов, то есть если элементы  и
и  принадлежат данному множеству (
принадлежат данному множеству (  ,
, 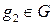 ), то их произведение также принадлежит множеству
), то их произведение также принадлежит множеству  ).
).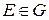 такой, что выполняется
такой, что выполняется 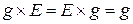 .
. имеется ему обратный
имеется ему обратный 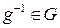 , так что
, так что  .
. .
. в точку с координатами
в точку с координатами  . Например, если мы посмотрим из центра элементарной ячейки с координатами [[1/2, 1/2, 1/2]], то в любом направлении
. Например, если мы посмотрим из центра элементарной ячейки с координатами [[1/2, 1/2, 1/2]], то в любом направлении  картина будет такой же, как и в направлении
картина будет такой же, как и в направлении 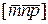 . Понятно, что в решетке все узлы являются центрами симметрии решетки.
. Понятно, что в решетке все узлы являются центрами симметрии решетки. называют воображаемую прямую, поворот кристалла вокруг которой на угол
называют воображаемую прямую, поворот кристалла вокруг которой на угол  совмещает его с самим собой.
совмещает его с самим собой. -го порядков. Кристалл может быть симметричным относительно многих пересекающихся осей, но возможные угловые соотношения между осями жестко ограничены.
-го порядков. Кристалл может быть симметричным относительно многих пересекающихся осей, но возможные угловые соотношения между осями жестко ограничены. со следующим поворотом вокруг оси В на угол
со следующим поворотом вокруг оси В на угол  может быть представлен единственным поворотом около некоторой третьей оси С на угол
может быть представлен единственным поворотом около некоторой третьей оси С на угол  [1]. Каждому из возможных сочетаний осей симметрии отвечает кристаллографическая система (сингония) (см. табл.1.1 и табл.2.2).
[1]. Каждому из возможных сочетаний осей симметрии отвечает кристаллографическая система (сингония) (см. табл.1.1 и табл.2.2). , зеркально поворотные –
, зеркально поворотные – 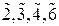 . Плоскости симметрии помечают символом
. Плоскости симметрии помечают символом  . Записи × (точка), : (двоеточие), / (косая черта) означают, что плоскость соответственно является параллельной, перпендикулярной или наклоненная под углом к оси симметрии. Центр инверсии помечают
. Записи × (точка), : (двоеточие), / (косая черта) означают, что плоскость соответственно является параллельной, перпендикулярной или наклоненная под углом к оси симметрии. Центр инверсии помечают  .
.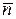 .
. – ось симметрии порядка
– ось симметрии порядка 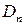 – ось симметрии порядка
– ось симметрии порядка 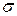 – плоскость симметрии;
– плоскость симметрии; – зеркально поворотная ось порядка
– зеркально поворотная ось порядка  – набор осей симметрии кубического тетраэдра;
– набор осей симметрии кубического тетраэдра;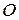 – набор осей симметрии кубического октаэдра;
– набор осей симметрии кубического октаэдра; – тождественное (единичное) превращение.
– тождественное (единичное) превращение. около символа
около символа