 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методика выполнения работы. Теоретическая часть
Теоретическая часть Всем реальным жидкостям присуще явление внутреннего трения или вязкости. При относительном перемещении слоев жидкости между ее слоями возникают силы внутреннего трения (вязкости), действующие таким образом, чтобы уравнять скорости всех слоев. Возникновение этих сил объясняется тем, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество движения, вследствие чего последний начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения, что приводит к его торможению. Рассмотрим жидкость, движущуюся в направлении оси x (рис.5.1). Пусть слои жидкости движутся с разными скоростями. На оси z возьмем две точки на расстоянии ∆
Рис. 5.1
Скорости слоев отличаются в этих точках на величину ∆υ. Отношение ∆υ/∆z характеризует изменение скорости слоев на единицу длины в направлении, перпендикулярном к поверхности слоя, и называется градиентом скорости. В случае установившегося (стационарного) течения модуль силы внутреннего трения F между двумя слоями, согласно формуле Ньютона, пропорциональна площади их соприкосновения ∆S и градиенту скорости ∆υ/∆z
Величина η называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Величина φ, обратная коэффициенту динамической вязкости η, называется текучестью. Если в формуле (5.1) положить численно ∆υ/∆z = 1, ∆S = 1, то F =η, т.е. коэффициент динамической вязкости - это физическая величина, численно равная силе внутреннего трения F, возникающей между двумя слоями жидкости с площадью соприкосновения ∆S, равной единице, движущимися один относительно другого с градиентом скорости ∆υ/∆z, равным единице. В СИ размерность [η] = кг·м-1·с-1 и единица измерения - Па·с (Паскаль ·секунда). Коэффициент динамической вязкости зависит от природы жидкости и для данной жидкости с повышением температуры η уменьшается. Вязкость играет существенную роль при движении жидкостей. Слой жидкости, непосредственно прилегающей к твердой поверхности, в результате прилипания остается неподвижным относительно нее. Скорость остальных слоев возрастает по мере удаления от твердой поверхности. Наличие слоя жидкости между трущимися поверхностями твердых тел способствует уменьшению коэффициента трения. Наряду с коэффициентом динамической вязкости η употребляется коэффициент кинематической вязкости ν = η / ρ, где ρ - плотность жидкости.
Методика выполнения работы Определение коэффициента внутреннего трения по методу Стокса заключается в наблюдении падения небольшого шарика в испытуемой жидкости. Экспериментальная установка состоит из двух стеклянных цилиндрических сосудов, расположенных симметрично относительно измерительной линейки и заполненных вязкими жидкостями. На измерительной линейке расположены два ползунка (верхний и нижний) с планками. Расстояние между планками равно L. Для каждой жидкости проводят серию опытов. В сосуд через отверстие в пробке опускают поочередно 5 небольших шариков, плотность которых ρ1 больше плотности жидкости ρ2. Диаметры шариков предварительно измеряют микрометром. Расстояние между поверхностью жидкости и верхней планкой подбирают так, чтобы на этом участке скорость шарика стабилизировалась, при этом на участке L между планками скорость шарика будет постоянной. В опыте измеряют диаметры шариков, расстояние между двумя планками и время движения каждого шарика на этом участке. На движущийся со скоростью υо шарик в вязкой жидкости действуют следующие силы:
Благодаря вязкости жидкости, шарик при падении увлекает прилегающие к нему слои жидкости и поэтому испытывает сопротивление (трение) со стороны жидкости. Равнодействующая сил, действующих на шарик по II закону Ньютона, будет
или в проекциях на вертикальное направление ma = F1 - F2 - Fc. (5.3) В начале движения шарика движение будет ускоренным. С ростом скорости растет и сила сопротивления, а ускорение шарика уменьшается. Наступит такой момент, когда действующие на шарик силы уравновесятся, ускорение станет равным нулю, а движение шарика - равномерным на участке L (рис. 5.2). При равномерном движении шарика формула (5.3) примет вид F1 - F2 - Fc = 0. (5.4) Подставляя в (5.4) выражения для сил F1 , F2 , Fc, а также учитывая, что объем шарика равен
тогда
Из соотношения (5.5), учитывая, что скорость равномерного движения шарика на участке L равна υ= L/t (где t - время движения шарика между планками), получим формулу для коэффициента внутреннего трения жидкости
Поиск по сайту: |
 z
z
 . (5.1)
. (5.1) Рис. 5.2
Рис. 5.2
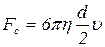 ,
где η - коэффициент вязкости жидкости, υ - скорость падения шарика, d - диаметр шарика.
,
где η - коэффициент вязкости жидкости, υ - скорость падения шарика, d - диаметр шарика.
 (5.2)
(5.2) ,
, . (5.5)
. (5.5)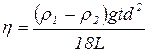 (5.6)
(5.6)