 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Деякі застосування подвійних інтегралів ⇐ ПредыдущаяСтр 3 из 3
І. Маса області. В попередніх параграфах було показано, що маса неоднорідної області
Якщо ж ІІ. Обчислення площ плоских областей. Покладемо в (1)
формула площі області
ІІІ. Обчислення об’єму тіла за допомогою подвійного інтеграла.Тіло, яке обмежене зверху поверхнею Об’єм вертикального циліндричного тіла знаходиться за формулою
Задача. Обчислити об’єм тіла, обмеженого двома поверхнями
Рис 1. Розв’язання. Перша з поверхонь – параболоїд обертання навколо осі Їх лінії перетину знаходимо із системи:
Отже обидві поверхні перетинаються по колу
Рис. 2. Шуканий об’єм
Далі обчислимо в полярних координатах:
. IV.Обчислення статичних моментів, координат центра мас та моментів інерції областей. Статичні моменти
Зауважимо, що за подібними формулами з теорії імовірностей знаходяться так звані математичні сподівання двовимірних випадкових величин. Координати центра маси плоскої області
де Моменти інерції
Задачі Знайти площі плоских областей, обмежених даними лініями 1. 2. 4. 6. 8. 10. 11. Відповіді: 1. 6. Обчислити об’єми тіл, обмежених даними лініями. 12. 13. 14. 15. 16. 17. 18. 19. Відповіді: 12. 17. 20. Знайти координати центра маси платівки, обмеженої параболою 21. Знайти центр мас однорідної платівки 22. Знайти центр мас однорідної платівки обмеженої параболами 23. Знайти центр мас плоскої однорідної фігури, обмеженої лініями
24. Обчислити момент інерції однорідного квадрата
25.Обчислити момент інерції однорідної фігури, обмеженої лініями Відповіді: 20. 22.
Поиск по сайту: |
 , в кожній площі якої визначена густина розподілу маси
, в кожній площі якої визначена густина розподілу маси  , знаходяться за формулою
, знаходяться за формулою . (1)
. (1) і є щільністю розподілу ймовірностей, то за формулою (1) обчислюється ймовірність попадання випадкової точки в область
і є щільністю розподілу ймовірностей, то за формулою (1) обчислюється ймовірність попадання випадкової точки в область  , тоді маса чисельно дорівнює площі області
, тоді маса чисельно дорівнює площі області 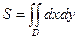 (2)
(2)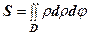 . (3)
. (3)
 , знизу – областю
, знизу – областю  площини
площини  , а збоку – циліндричною поверхнею, твірні якої проходять через границю області
, а збоку – циліндричною поверхнею, твірні якої проходять через границю області  і перетинають поверхню
і перетинають поверхню  , називається вертикальним циліндричним тілом(див. рис. 1)
, називається вертикальним циліндричним тілом(див. рис. 1) . (4)
. (4) і
і  .
.
 , напрямлений вниз, друга поверхня – конус обертання навколо
, напрямлений вниз, друга поверхня – конус обертання навколо  , напрямлений – вверх.
, напрямлений – вверх.
 - не підходить. Якщо
- не підходить. Якщо  , то, наприклад, друге рівняння запишеться
, то, наприклад, друге рівняння запишеться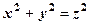 .
.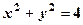 , яке знаходиться на площині
, яке знаходиться на площині 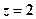 , перпендикулярній
, перпендикулярній  (див. рис. 2).
(див. рис. 2).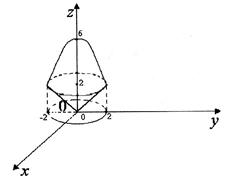
 тіла дорівнює різниці об’ємів двох циліндричних тіл
тіла дорівнює різниці об’ємів двох циліндричних тіл  і
і  . Основа обох циліндрів – круг радіуса
. Основа обох циліндрів – круг радіуса  з центром в
з центром в  на площині
на площині 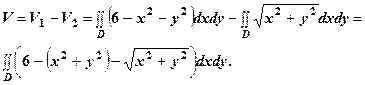 .
.

 і
і  знаходяться за формулами
знаходяться за формулами ,
,  . (5)
. (5) ,
,  , (6)
, (6)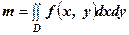 - маса області.
- маса області.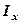 і
і  відносно координатних осей
відносно координатних осей  і
і  і момент інерції
і момент інерції  відносно початку координат знаходяться відповідно за формулами
відносно початку координат знаходяться відповідно за формулами ,
, 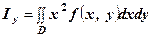 , (7)
, (7) . (8)
. (8) .
. . 3.
. 3. 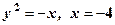 .
. 5.
5. 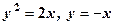 .
. . 7.
. 7.  .
. . 9.
. 9. 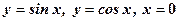 .
.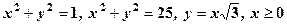 .
.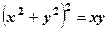 .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  .
. .
. .
.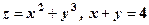 та координатними площинами.
та координатними площинами.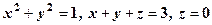 .
. .
. .
. .
. .
. . 13.
. 13.  . 14.
. 14.  . 15.
. 15.  . 16.
. 16.  .
. 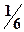 . 18.
. 18. 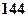 . 19.
. 19.  .
. і прямою
і прямою  , якщо густина розподілу маси в кожній точці дорівнює ординаті точки.
, якщо густина розподілу маси в кожній точці дорівнює ординаті точки. , обмеженої лініями
, обмеженої лініями 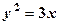 та
та  .
. .
. .
. відносно початку координат.
відносно початку координат. , відносно вісі
, відносно вісі  . 21.
. 21.  .
.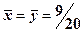 . 23.
. 23. 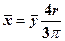 . 24.
. 24. 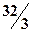 . 25.
. 25.  .
.