 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Поверхневий натяг рідини
Тема: Властивості рідини План 1. Поверхневий натяг рідини. 2. Змочування. 3. Капілярні явища. Основна література: 1. Л.Є.Генденштейн, І.Ю.Ненашев Фізика,10кл.: Підруч. для загальноосвіт. навч. Закл: Рівень стандарту: Гімназія,2010.С 210-214 Додаткова література: 2. Жданов Л.С., Жданов Г.Л. Фізика. Підручник для середніх спеціальних навчальних закладів. - К.: Вища школа, 1983.С 94-100 Ключові поняття:
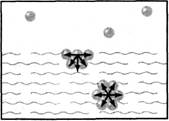
Поверхневий натяг рідини. Всі ви, напевне, милувалися маленькими краплями роси, які на листках рослин набувають форми майже правильних кульок. Це явище спостерігав ще Г. Галілей, якого дуже дивувало, чому великі краплі води не розпливаються по всьому листку капусти, а набувають форми маленьких кульок. Таку ж форму мають краплі води на парафіні чи жирній поверхні, пролита на стіл ртуть тощо. Якщо ці краплі стикаються, вони зливаються в одну краплю, форма якої також наближається до кулястої. У космічному кораблі, який перебуває в стані невагомості, кулястої форми набувають не тільки окремі краплі, а й великі об'єми рідини. Ці явища здаються дуже дивними. Адже ми звикли, що рідина набуває форми посудини, в якій вона знаходиться, і власної форми не має. Виявляється, що так буває не завжди. Галілей спостерігав, як змащена жиром голка може плавати на воді і як легкі комахи-водомірки швидко ковзають по поверхні води, як ковзанярі по льоду. Ці спостереження начебто суперечать існуванню архімедової сили. Але якщо голка прорве поверхню рідини, вона тоне, як і має бути під час дії архімедової сили. Як пояснити ці явища? Покладемо лезо безпечної бритви, трохи вкрите жиром, на поверхню води. Воно не тоне. Коли лезо «плаває» на воді, то можна помітити невелике прогинання поверхні води. Якщо лезо занурити в глиб води, воно піде на дно. Це означає, що властивості поверхні рідини відрізняються від властивостей решти рідини. Як це можна пояснити? Вся справа в тому, що молекули на поверхні рідини перебувають в інших умовах, ніж молекули всередині рідини. На кожну молекулу всередині рідини діють сили притягання з боку сусідніх молекул, які оточують її з усіх боків (мал.1).
Мал.1 Результуюча цих сил дорівнює нулю. Над поверхнею рідини знаходиться пара, густина якої в багато разів менша за густину рідини, і взаємодією молекул пари з молекулами рідини можна знехтувати. Молекули на поверхні притягуються лише молекулами, які лежать нижче. Тому рівнодійна сил притягання, які діють на молекули поверхневого шару, не дорівнює нулю. Під дією цих сил молекули поверхневого шару втягуються всередину, кількість молекул на поверхні зменшується, і площа скорочується. Однак усі молекули не можуть втягнутися всередину. На поверхні залишається така кількість молекул, за якої площа поверхні виявляється мінімальною за даного об'єму рідини. Ось чому рідини під дією молекулярних сил набувають сферичної форми, за якої поверхня мінімальна. 1.
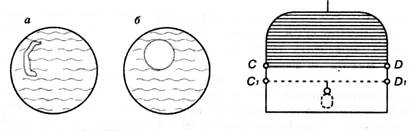
Скорочення поверхні рідини під впливом притягання її молекул всередину рідини відбувається так, ніби вздовж її поверхні діяла сила і викликала її скорочення. Цю силу називають силою поверхневого натягу. Для виявлення дії сили поверхневого натягу скористаємося властивістю деяких рідин, наприклад мильної води, створювати тонкі плівки. Якщо опустити в мильну воду дротяне кільце і вийняти його, то воно затягується мильною плівкою — тонким шаром рідини. Покладемо на цю плівку невелику петельку з шовкової нитки (мал.2, а) і проткнемо плівку в області, охопленій петелькою. Відразу ж оточуюча петельку мильна плівка, діючи на всі її елементи з однаковою силою, розтягне її і надасть їй форму кола (мал. 2, б). Візьмемо вертикальний прямокутний дротяний каркас (мал. 3), одна сторона якого (CD) рухома, і також утворимо на ньому мильну плівку. Якщо дати змогу рухомій стороні каркаса вільно переміщатися, вона під час скорочення плівки підніматиметься вгору. Щоб утримати її у початковому положенні C1D1, треба прикласти до неї достатню силу, наприклад підвісити невеликий тягарець. Це означає, що з боку мильної плівки на горизонтальну частину каркаса CD діє сила, яка намагається скоротити поверхню плівки. За модулем ця сила дорівнює вазі тягарця, яка зрівноважує її. Отже, сила поверхневого натягу — це сила, яка діє вздовж поверхні рідини, перпендикулярно до лінії, якаобмежує поверхню, і спрямована в бік її скорочення.
Мал.2 Мал.3 Якщо проводити дослід з каркасами різних розмірів, то можна виявити, що абсолютна величина сили поверхневого натягу F пропорційна довжині l рухомої сторони каркаса, а відношення F/lдля плівки з даної рідини завжди одне й те саме. Не залежить воно і від матеріалу каркаса. Отже, відношення сили поверхневого натягу, яка діє на межі поверхні рідини, до довжини цієї межі характеризує вільну поверхню самої рідини. Відношення сили поверхневого натягу до довжини периметра, який обмежує поверхню рідини, називається поверхневим натягом. Цю величину позначають літерою Ϭ:
З формули
2.
Мал.4 Обчислимо додатковий тиск для сферичної поверхні рідини. Для цього мислено перетнемо сферичну каплю на дві півкулі. Поверхнева плівка цих двох півкуль обмежена колом 2πR, де R- радіус краплі. Внаслідок поверхневого натягу обидві півкулі притягуються одна до одної з силою
за нею визначається додатковий тиск під опуклою сферичною плівкою рідини. Поверхневий натяг істотно залежить від домішок до рідин. Поверхнево-активними (ПАР)- речовинами, це речовини які послаблюють поверхневий натяг рідини. Для води поверхнево-активними речовинами є етиловий спирт, ефір, мило, різні пральні порошки. Вони сильно знижують її поверхневий натяг (приблизно з 7,5•10-2 до 4,5•10-2 Н/м). Це полегшує миття і прання білизни, оскільки високий поверхневий натяг чистої води не дає їй проникати між волокнами тканини і в дрібні пори. Змочування. У процесі прання білизни значення s зменшується як через нагрівання рідини, так і внаслідок введення мийних засобів. Якщо рідина межує з її парою, то взаємодії між молекулами слабкіші і їх можна не враховувати. Коли поверхневий шар рідини межує з твердим тілом, то взаємодію молекул рідини і твердого тіла слід враховувати. У повсякденному житті можна спостерігати, що крапля води розпливається по чистій поверхні скла (Мал.5, а), але не розпливається по забрудненій жиром поверхні і має при цьому форму майже правильної кулі (Мал.5, б). У першому випадку говорять, що вода змочує поверхню, у другому - не змочує.
Мал.5
3.
Інтенсивність змочування характеризується кутом змочування Q, який утворюється між дотичною до поверхні рідини і поверхнею твердого тіла. Відлік кута виконують у бік рідини. Якщо
Явища змочування і незмочування відіграють важливе значення в побуті і техніці, якби вода не змочувала тіло людини, то марним було б купання. Добре змочування потрібне під час фарбування і прання, паяння, збагачення руд цінних порід та інших технічних процесів. Капілярні явища. Явище змочування і незмочування виявляється у піднятті і спусканні рідини в тонких трубках (капілярах). Розглянемо капілярні явища. Опустимо в рідину густиною r капіляр радіусом r 1 мм (Мал.6).
Мал.6 Якщо діаметри трубок невеликі, то майже вся поверхня води в них буде викривленою. Викривлену поверхню називають меніском, вузенькі трубки – капілярними, а підняття рідини в них – явищем капілярності, або просто капілярністю. Висоту підняття рідини в капілярних трубках можна легко обчислити. Якщо рідина повністю змочує стінки трубки, її меніск можна прийняти за півсферу, радіус меніска дорівнюватиме радіусові капіляра, а надмір тиску Під дією цього тиску рідина піднімається на таку висоту
Цю формулу застосовують і до капілярної трубки із незмочуючою рідиною, тільки в цьому випадку обчислюється висота не підняття, а опускання в ній рідини. Задачі для розв’язування: 1. У 5 2. Відомо, що t =25 °C, ρ 3. При температурі 25 °С відносна вологість повітря становить 55%. Яку абсолютну вологість має повітря? 4. За температури 15°С, абсолютна вологість = 6,4 Запитання для самоконтролю: 1. Які властивості має поверхневий шар рідини? 2. Що називають поверхневим натягом? 3. Виконавши рисунок, установіть фізичний зміст поверхневого натягу як величини, пов'язаної з енергією поверхневого шару рідини. 4. Наведіть приклади дії сил поверхневого натягу. 5. Що називають коефіцієнтом поверхневого натягу? Від чого він залежить? У яких одиницях виміряється коефіцієнт поверхневого натягу в СІ? 6. Що являє собою сила поверхневого натягу? Яка формула виражає зміст цього поняття? 7. Як зміниться сила поверхневого натягу води у разі розчинення в ній мила? 8. Якої форми набувають краплі рідини в умовах невагомості? Чому? 9. Виконавши пояснювальний рисунок, розкрийте фізичну сутність явищ змочування і незмочування. 10. Чому жирові плями на одязі не вдається змити водою? 11. Що називають меніском? 12. Що таке крайовий кут? Яким є його значення у разі змочування? Незмочування? 13. Що називають капілярністю? 14. Обґрунтуйте, у якому випадку рідина в капілярі піднімається, а в якому опускається. 15. Чому фундамент цегляних будинків покривають гарячим бітумом чи обкладають толем? 16. Виведіть формулу, за якою визначають висоту піднімання чи опускання рідини в капілярі. 17. Наведіть приклади врахування і використання капілярних систем у повсякденному житті. Задачі для розв’язування: 1. У 5 2. Відомо, що t =25 °C, ρ 3. При температурі 25 °С відносна вологість повітря становить 55%. Яку абсолютну вологість має повітря? 4. За температури 15°С, абсолютна вологість = 6,4 Задачі для розв’язування: 1. У 5 2. Відомо, що t =25 °C, ρ 3. При температурі 25 °С відносна вологість повітря становить 55%. Яку абсолютну вологість має повітря? 4. За температури 15°С, абсолютна вологість = 6,4
Задачі для розв’язування: 1. У 5 2. Відомо, що t =25 °C, ρ 3. При температурі 25 °С відносна вологість повітря становить 55%. Яку абсолютну вологість має повітря? 4. За температури 15°С, абсолютна вологість = 6,4
Поиск по сайту: |
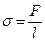

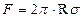 . Вона притискає їх одну до одної на поверхні
. Вона притискає їх одну до одної на поверхні 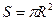 , і отже, обумовлює додатковий тиск:
, і отже, обумовлює додатковий тиск: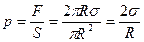 - формула Лапласа
- формула Лапласа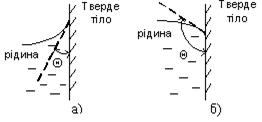
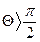 - поверхня тіла змочувана, а якщо
- поверхня тіла змочувана, а якщо 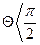 - не змочувана.
- не змочувана.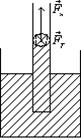
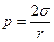 .
. , щоб її гідростатичний тиск
, щоб її гідростатичний тиск 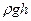 зрівноважував надмір тиску
зрівноважував надмір тиску 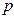 :
: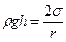 ;
;  - висота підняття рідини в капілярній трубці прямо пропорційна поверхневому натягу і обернено пропорційна радіусу трубки і густині рідини.
- висота підняття рідини в капілярній трубці прямо пропорційна поверхневому натягу і обернено пропорційна радіусу трубки і густині рідини.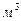 повітря міститься 80 г водяної пари. Визначити абсолютну вологість.
повітря міститься 80 г водяної пари. Визначити абсолютну вологість. = 12
= 12 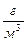 ρ
ρ 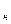 =23
=23 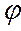 .
. = 12
= 12 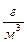 ρ
ρ 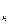 =23
=23