 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Інтеграли з нескінченними межами інтегрування (невласні інтеграли першого роду)
Нехай функція У цьому випадку інтеграл називають збіжним, а підінтегральну функцію Аналогічно визначається невласний інтеграл на проміжку а також де Ознаки збіжності невласних інтегралів першого роду Ознака порівняння Якщо на проміжку Гранична ознака порівняння Якщо існує границя то інтеграли 3, Абсолютна збіжність Якщо інтеграл . Невласні інтеграли від необмежених функцій (невласні інтеграли другого роду) Нехай функція то її називають невласним інтегралом другого родуі позначають У цьому випадку кажуть, що інтеграл існує, або збігається. Якщо границя нескінченна або не існує, то інтеграл також називають невласним інтегралом, але розбіжним. Аналогічно, якщо Якщо Ознаки збіжності невласних інтегралів другого роду аналогічні подібним ознакам для невласних інтегралів першого роду.
Обчислити значення невласних інтегралів першого роду або встановити їх розбіжність.
Приклад 1
Невласний інтеграл разбіжний.
Приклад 2
інтеграл збіжний.
Приклад 3
Перейдемо до границі
Виділимо повний квадрат в знаменнику
Отримаємо
Зробимо заміну
В результаті матимемо
Понизимо порядок косинуса за формулою
Зробимо зворотну заміну
Враховуючи на поведінку функції
Тобто даний невласний інтеграл збіжний. Приклад 4
Так як верхня межа є
Проведемо деякі перетворення:
Згідно правил інтегрування, матимемо
Підставляючи межі
та переходячи до границі, остаточно отримаємо
Отже, даний інтеграл збіжний. Приклад 5
Проінтегруємо частинами, покладаючи
І остаточно отримаємо
Отже, наш інтеграл збіжний.
Обчислити інтеграли від необмежених функцій (невласні інтеграли другого роду) або встановити їх розбіжність.
Приклад 1
Підінтегральна функція має нескінчений розрив в точці
Тепер, так як підінтегральна функція є неперервна, проведемо інтегрування за формулою Ньютона-Лейбніца.
І остаточно
Даний інтеграл розбіжний. Приклад 2
Розкладемо знаменник на прості множники:
Як бачимо, в точці
Розкладемо підінтегральний дріб на прості дроби, скориставшись методом невизначених коефіцієнтів:
І остаточно
Приклад 3
Проведемо деякі перетворення даного інтеграла і перейдемо до границі при
Зробимо заміну
Проінтегруємо частинами
І остаточно
тобто даний інтеграл розбіжний. Приклад 4
Як бачимо, підінтегральний вираз має розриви в точках
Зробимо заміну
В результаті отримаємо
Понизивши порядок синуса та використавши таблицю інтегралів отримаємо
Зробивши зворотну заміну
Переходячи до границі в дужках отримаємо
І остаточно
Тобто, наш інтеграл є збіжний.
Інтеграли з безкінечними межами (інтеграли першого роду) В даних задачах визначити не власні інтеграли (або дослідити їх на збіжність) 1. 3. 5. 7. 9. 11.
Різні задачі 12.При яких значеннях k інтеграл
буде збіжним? 13.При яких значеннях k збігаються інтеграли 1) Вирахувати не збіжні інтеграли 14. 15. 16. 17. 18. 19.Вирахувати інтеграл В наступних задачах обчислити інтеграли, користуючись формулами
20. 22. 24. Обчислити інтеграл 26. 28. В даних задачах дослідити на збіжність наступні інтеграли 30. 32. 34. 36.
Інтеграли функцій з нескінченними розривами. Обчислити невласні інтеграли (або встановити їх збіжність) 37. 39. 41. 43. 45. Дослідити на збіжність інтеграли 46. 48. Розділ 3
Поиск по сайту: |
 визначена на проміжку
визначена на проміжку  та інтегрована на будь-якому відрізку
та інтегрована на будь-якому відрізку 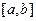 , де
, де 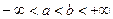 . Тоді, якщо існує скінчена границя
. Тоді, якщо існує скінчена границя  , її називають невласним інтегралом першого роду і позначають
, її називають невласним інтегралом першого роду і позначають  . Таким чином, за означенням
. Таким чином, за означенням .
. . Якщо ж границя не існує або нескінченна, то інтеграл називається також невласним, але розбіжним.
. Якщо ж границя не існує або нескінченна, то інтеграл називається також невласним, але розбіжним.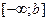 :
: ,
, ,
, - довільне дійсне число.
- довільне дійсне число. неперервні та задовольняють умову
неперервні та задовольняють умову  , то із збіжності інтеграла
, то із збіжності інтеграла  випливає збіжність інтеграла
випливає збіжність інтеграла  , а із розбіжності інтеграла
, а із розбіжності інтеграла  випливає розбіжність інтеграла
випливає розбіжність інтеграла  ,
, 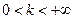 ,
,  ,
,  ,
, або одночасно обидва збігаються, або одночасно розбігаються.
або одночасно обидва збігаються, або одночасно розбігаються. збігається, то збіжним є і інтеграл
збігається, то збіжним є і інтеграл 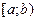 . Точку
. Точку  назвемо особливою точкою функції
назвемо особливою точкою функції 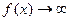 при
при  . Нехай функція
. Нехай функція 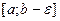 при довільному
при довільному  такому, що
такому, що  . Тоді, якщо існує скінчена границя
. Тоді, якщо існує скінчена границя ,
, . Отже, за визначенням
. Отже, за визначенням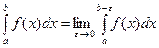 .
. - особлива точка, то
- особлива точка, то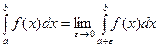 .
. , то
, то .
. - не існує.
- не існує. -
-

 .
.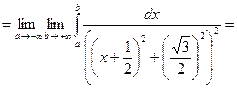
 ;
; 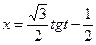 ;
;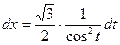 .
.
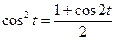 :
:

 .
.
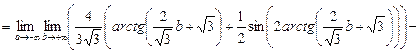

 на нескінченостях, остаточно отримаємо
на нескінченостях, остаточно отримаємо
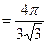 .
.
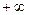 , введемо змінну
, введемо змінну  , і отримаємо
, і отримаємо


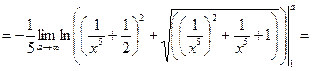
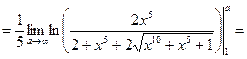

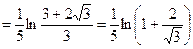 .
.
 ,
, 


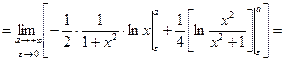

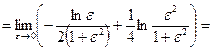
 .
.
 , яка належить проміжку інтегрування. Тому перейдемо до границі при
, яка належить проміжку інтегрування. Тому перейдемо до границі при 
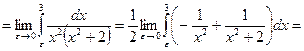


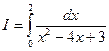

 , яка належить проміжку інтегрування, знаменник перетворюється в нуль і підінтегральна функція має нескінченний розрив. Перейдемо до границі при
, яка належить проміжку інтегрування, знаменник перетворюється в нуль і підінтегральна функція має нескінченний розрив. Перейдемо до границі при 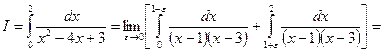


 .
.

 . Отримаємо
. Отримаємо


 ,
,
 та
та  . Перейдемо до границі при
. Перейдемо до границі при 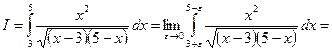

 ,
,  ,
, 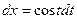 .
.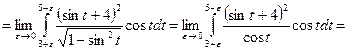
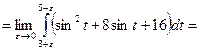


 , матимемо
, матимемо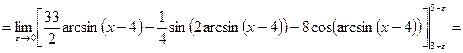


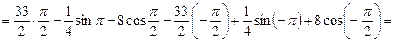
 .
. 2.
2. 
 ,
,  4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 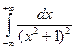


 2)
2)  ?
?
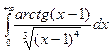
 (n-ціле додатне число)
(n-ціле додатне число) (n-ціле додатне число)
(n-ціле додатне число) (n-ціле додатне число)
(n-ціле додатне число)
 (інтеграл Пуассона)
(інтеграл Пуассона) (інтеграл Діріхлє).
(інтеграл Діріхлє). 21.
21. 
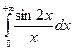 23.
23. 
 25.
25. 
 27.
27. 
 29.
29. 
 31.
31. 
 33.
33. 
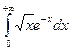 35.
35. 

 38.
38. 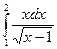
 40.
40. 
 42.
42. 
 44.
44. 

 47.
47. 
