|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Методи наближеного обчислення ⇐ ПредыдущаяСтр 2 из 2
Для деяких неперервних надінтегральних функцій f (х) первісну не можна виразити елементарними функціями. У цих випадках обчислення визначного інтеграла за формулою Ньютона-Лейбніца неможливе. Крім того, у практичній діяльності часто досить знати лише наближене значення визначеного інтеграла і знаходити це наближене значення такими методами, які дозволяють використовувати сучасну обчислювальну техніку. Тому математики багатьох країн розробляють ефективні методи наближеного обчислення визначеного інтеграла. Найбільш часто використовують три методи — метод прямокутників, метод трапецій та метод парабол (метод Сімпсона). Якщо відрізок інтегрування [а,b] поділити на n рівних частин довжиною
яку називають формулою прямокутників. Чим більше буде n, тим менше буде крок Якщо поділити відрізок інтегрування точками ділення а = х0 < x1 < х2 < ... < хk < ... < хn-1 < хk = b на n рівних частин довжиною
яку називають формулою трапецій. Легко бачити, що при зростанні n крок Якщо відрізок інтегрування [а,b] поділити на парну кількість рівних частин (тобто n = 2m) i позначити уk = f (xk), де xk = а +
яку називають формулою Сімпсона. Ця формула дає більш точне значення визначеного інтеграла тому, що для її доведення використовується метод парабол, за яким на кожному відрізку [xk-1, xk] три значення функції f (х) входять до інтегральної суми. Застосування визначених інтегралів Обчислення площ Якщо на відрізку [а,b] функція f (х)
Якщо на відрізку [a, b] функція f (х)
Якщо f (х) на відрізку [а,b] декілька разів змінює свій знак, то інтеграл по відрізку [а,b] треба розбити на суму інтегралів по часткових відрізках. Інтеграл буде додатним на тих відрізках, де f (х) Щоб одержати суму площ (без врахування розташування відносно осі 0х) треба знайти суму абсолютних величин інтегралів по часткових
Мал. 2 відрізках або обчислити інтеграл від абсолютного значення функції, тобто
Приклад 1. Обчислити площу фігури, обмеженої еліпсом
Розв'язування. Із аналітичної геометрії відомо, що цей еліпс має вигляд такий, як на Малюнку 3. Шукана площа S дорівнює 4S1, де S1 — площа заштрихованої частини еліпса, що розташована у першому квадранті. Отже,
Із рівняння еліпса знаходимо у:
Мал. 3. Для заштрихованої частини еліпса у
Заміна x = sin t дає: dx = cost · dt; t = arcsin x,
Отже,
За формулою (13) одержимо S = 8 · Якщо треба обчислити площу фігури, обмеженої кривими y = f1(х), y=f2(х) та прямими х = а, х = b (дивись, наприклад, Малюнок 4), то при f1(х)
Мал. 4
Приклад 2. Обчислити площу фігури, обмеженої лініями
Розв'язування. Спочатку зобразимо фігуру, площу якої треба знайти (Мал. 5). Знайдемо точку перетину цих парабол. Координати точок перетину задовольняють обом рівнянням, тому
Мал. 5 Отже, площа заштрихованої фігури буде
(квадратних одиниць).
Поиск по сайту: |
 і позначити через
і позначити через  середню точку відрізку
середню точку відрізку 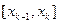 визначений інтеграл можна обчислити за формулою
визначений інтеграл можна обчислити за формулою (10)
(10) (11)
(11) х·k — точки ділення, k = 0, 1, ..., 2m, тоді визначений інтеграл можна обчислити за формулою
х·k — точки ділення, k = 0, 1, ..., 2m, тоді визначений інтеграл можна обчислити за формулою (12)
(12) 0, то згідно з формулою (4), обчислення площі криволінійної трапеції, зображеної на малюнку 1, можна знайти за формулою
0, то згідно з формулою (4), обчислення площі криволінійної трапеції, зображеної на малюнку 1, можна знайти за формулою
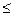 0, то криволінійна трапеція, обмежена кривою f (х), відрізком [а, b] та прямими х = аі х = b, буде розташована нижче осі 0х. Визначений інтеграл
0, то криволінійна трапеція, обмежена кривою f (х), відрізком [а, b] та прямими х = аі х = b, буде розташована нижче осі 0х. Визначений інтеграл 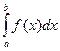 у цьому випадку буде
у цьому випадку буде  або
або  (f(x)
(f(x) 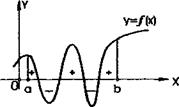


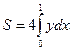


 і ми одержуємо
і ми одержуємо (1)
(1)
 tB = arcsin1 =
tB = arcsin1 =  .
.

 (квадратних одиниць).
(квадратних одиниць). (14)
(14)
 та
та