Розділ 4. Інтеграл Лебега
Нагадаємо, що інтеграл Рімана  визначається як границя інтегральних сум: визначається як границя інтегральних сум: 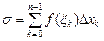 , де , де 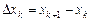 , , 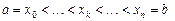 і і 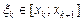 . Проте, ряд достатньо простих функцій не є інтегровними за Ріманом. До таких належать, зокрема, функція . Проте, ряд достатньо простих функцій не є інтегровними за Ріманом. До таких належать, зокрема, функція 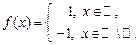 Інтеграл Лебега є узагальненим інтегралом Рімана. Основна ідея побудови інтеграла Лебега полягає в тому, що Інтеграл Лебега є узагальненим інтегралом Рімана. Основна ідея побудови інтеграла Лебега полягає в тому, що  множиться не на множиться не на  , а на міру множини тих , а на міру множини тих 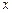 , в яких функція , в яких функція 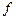 приймає значення близькі до приймає значення близькі до  . Завдяки цьому інтегрованими за Лебегом на множині скінченої міри є, зокрема, всі вимірні обмежені функції, до яких належить вище вказана функція. Далі введемо поняття інтеграла Лебега функції . Завдяки цьому інтегрованими за Лебегом на множині скінченої міри є, зокрема, всі вимірні обмежені функції, до яких належить вище вказана функція. Далі введемо поняття інтеграла Лебега функції  , якщо , якщо 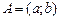 і і 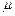 –лінійна міра Лебега на –лінійна міра Лебега на 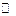 . Відповідні не змінюються суттєво, якщо . Відповідні не змінюються суттєво, якщо  –довільна вимірна множина і –довільна вимірна множина і 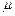 –довільна зліченно-адитивна, –довільна зліченно-адитивна,  -скінченна міра. -скінченна міра.
1. Прості функції.Функція  називається простою на множині називається простою на множині  , якщо її множина значень , якщо її множина значень 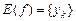 на на  є скінченною або зліченною. Графік простої функції складається з точок і відрізків паралельних осі є скінченною або зліченною. Графік простої функції складається з точок і відрізків паралельних осі 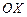 . Наприклад, функція . Наприклад, функція 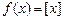 є простою. є простою.
Теорема 1. Для того щоб функція  , множина значень , множина значень 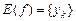 якої є скінченною або зліченною, була вимірною, необхідно і достатньо, щоб всі множини якої є скінченною або зліченною, була вимірною, необхідно і достатньо, щоб всі множини 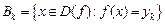 були вимірними. були вимірними.
Доведення. Нехай 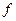 – вимірна функція. Оскільки – вимірна функція. Оскільки
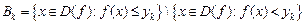 , ,
то 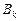 мусить бути вимірною. Нехай усі множини мусить бути вимірною. Нехай усі множини 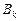 є вимірними. Тоді для кожного є вимірними. Тоді для кожного 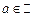 множина множина 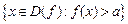 є об’єднанням скінченної або зліченної кількості множин є об’єднанням скінченної або зліченної кількості множин 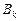 і, отже, є вимірною множиною. ► і, отже, є вимірною множиною. ►
Теорема 2. Для того щоб функція  була вимірною на множині була вимірною на множині  , необхідно і достатньо, щоб множина , необхідно і достатньо, щоб множина  була вимірною, була вимірною,  і існувала послідовність і існувала послідовність 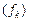 простих вимірних на простих вимірних на  функцій функцій 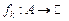 , яка рівномірно на , яка рівномірно на  збігається до збігається до 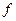 . .
Доведення. Достатність випливає з властивостей вимірних функцій. Доведемо необхідність. Нехай 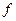 – вимірна на – вимірна на  і і  , якщо , якщо  , де , де 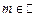 і і 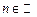 . Тоді . Тоді  , , 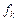 – прості вимірні функції, – прості вимірні функції, 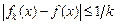 для всіх для всіх  і і  рівномірно на рівномірно на  .► .►
2. Означення і найпростіші властивості інтеграла Лебега простої функції по множині скінченої міри. Нехай  –вимірна множина скінченної міри, –вимірна множина скінченної міри,  – проста вимірна функція, – проста вимірна функція, 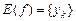 – множина її значень, – множина її значень, 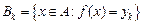 . Інтегралом Лебега простої функції . Інтегралом Лебега простої функції  по по  множині скінченної міри називається ряд: множині скінченної міри називається ряд:
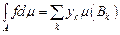 . (1) . (1)
Проста функція 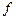 називається інтегрованою або сумовною на множині називається інтегрованою або сумовною на множині  , якщо ряд (1) є абсолютно збіжним. , якщо ряд (1) є абсолютно збіжним.
Теорема 1. Якщо  – сукупність скінченної або зліченної кількості вимірних попарно неперетинних множин, – сукупність скінченної або зліченної кількості вимірних попарно неперетинних множин, 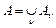 –множина скінченої міри, то для кожної простої функції –множина скінченої міри, то для кожної простої функції 
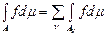 (2) (2)
причому з існування інтеграла в лівій частині випливає існування інтегралів в правій і абсолютна збіжність ряду(2). Навпаки, з абсолютної збіжності ряду (2) випливає інтегрованість 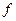 на множині на множині  . .
Доведення. Нехай 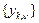 – множина значень функції – множина значень функції 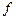 на множині на множині 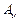 , , 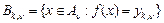 . Тоді . Тоді
 . .
Множини 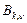 попарно неперетинні, попарно неперетинні, 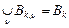 і і  , ,
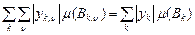 , , 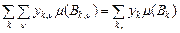 . .
Звідси та означення інтеграла простої функції випливає твердження теореми. ►
Теорема 2. 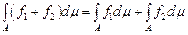 , якщо останні два інтеграли існують. , якщо останні два інтеграли існують.
Теорема 3. 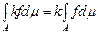 для будь-якої числової сталої для будь-якої числової сталої 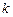 , якщо останній інтеграл існує. , якщо останній інтеграл існує.
Теорема 4.  для будь-яких чисел для будь-яких чисел  і і 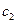 , якщо останні інтеграли існують. , якщо останні інтеграли існують.
Теорема 5.Якщо  – проста інтегрована функція, то – проста інтегрована функція, то
 . .
Теорема 6. Якщо 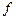 проста функція і проста функція і 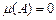 , то , то
 . .
Теорема 7.  для будь-якої вимірної множини для будь-якої вимірної множини  . .
Теорема 8. Якщо проста невід’ємна на  функція функція  є інтегрованою на є інтегрованою на  , то , то
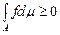 . .
Теорема 9. Якщо  вимірна проста функція, то вимірна проста функція, то
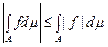 . .
Приклад 1. 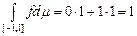 , якщо , якщо 
Приклад 2. Якщо 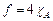 , , 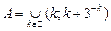 , то функція , то функція 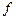 є простою, є простою,  , , 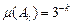 , , 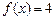 для для 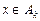 і і
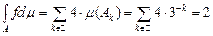 . .
3. Означення сумовної функції і її інтеграла Лебега на множині скінченної міри. Нехай  – множина скінченної міри. Функцію – множина скінченної міри. Функцію  назвемо сумовною або інтегрованою за Лебегом на множині назвемо сумовною або інтегрованою за Лебегом на множині  за мірою за мірою 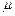 , якщо , якщо 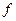 є вимірною на є вимірною на  і існує послідовність і існує послідовність 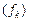 простих інтегрованих на простих інтегрованих на  функцій функцій 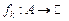 , яка рівномірно на , яка рівномірно на  збігається до збігається до 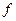 . Границю . Границю
 (1) (1)
назвемо інтегралом Лебега функції 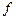 по множині по множині  за мірою за мірою 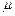 . .
Наступні три теореми обґрунтовують коректність цього означення.
Теорема 1. Границя (1) для будь-якої рівномірно збіжної на множині  послідовності послідовності 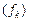 простих інтегрованих на простих інтегрованих на  функцій функцій 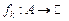 існує. існує.
Доведення. Справді, нехай  . Тоді . Тоді
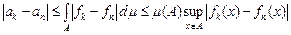 . ( 2) . ( 2)
Оскільки рівномірна збіжність на  рівносильна збіжності за рівносильна збіжності за  – нормою на – нормою на  , а збіжна послідовність є фундаментальною, то з (2) випливає фундаментальність, а тому і збіжність, в , а збіжна послідовність є фундаментальною, то з (2) випливає фундаментальність, а тому і збіжність, в 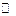 послідовності послідовності 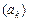 . Отже, границя (1) існує. ► . Отже, границя (1) існує. ►
Теорема 2. Границя (1) не залежить від вибору послідовності 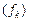 . .
Доведення. Якщо 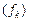 і і  – дві рівномірно збіжні до – дві рівномірно збіжні до 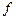 на на  послідовності простих інтегровних функцій, то такою ж є послідовність послідовності простих інтегровних функцій, то такою ж є послідовність
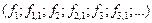 (3) (3)
Послідовність (3) також рівномірно збігається на  до до 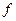 . Отже, за теоремою 1 для неї існує границя (1). Але послідовності . Отже, за теоремою 1 для неї існує границя (1). Але послідовності 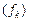 і і  є підпослідовностями послідовності (3). Звідси випливає твердження теореми 2. ► є підпослідовностями послідовності (3). Звідси випливає твердження теореми 2. ►
Теорема 3. Якщо 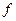 – проста функція, то означення інтеграла (1) співпадає з раніше наведеним. – проста функція, то означення інтеграла (1) співпадає з раніше наведеним.
Доведення. Справді, досить взяти сталу послідовність  .► .►
Приклад 1. Якщо 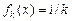 для для 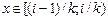 , то функції є простими на множині , то функції є простими на множині  і послідовність і послідовність 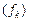 рівномірно на рівномірно на 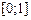 збігається до функції збігається до функції 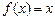 . При цьому, . При цьому,
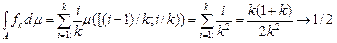 . .
Тому  . .
4. Найпростіші властивості інтеграла Лебега по множині скінченної міри. Нехай  – множина скінченної міри. – множина скінченної міри.
Теорема 1.  . .
Доведення. Це випливає безпосередньо з означення, оскільки функція  є простою. ► є простою. ►
Теорема 2 (однорідність). Для будь-якої сталої  виконується виконується
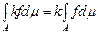 , ,
якщо останній інтеграл існує.
Доведення. Ця властивість випливає з означення і відповідної властивості інтеграла простих функцій, і одержуються за допомогою граничного переходу. ►.
Отож, отримуємо наступні сім тверджень.
Теорема 3. Якщо функція  є інтегровною на є інтегровною на  і і 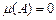 , то , то  . .
Теорема 4. (адитивність). 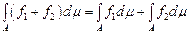 , ,
якщо останні два інтеграли існують.
Теорема 5. Для кожної інтегровної на  функції функції 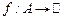
 . .
Теорема 6 (лінійність). Для будь-яких сталих 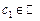 і і 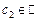
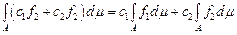 , ,
якщо останні інтеграли існують.
Теорема 7. Якщо функція  є інтегровною на є інтегровною на  і невід’ємною на і невід’ємною на  , то , то 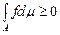 . .
Теорема 8. Якщо 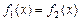 майже скрізь на майже скрізь на  , то , то
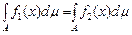 , ,
якщо принаймні один із цих інтегралів існує.
Теорема 9. Якщо функція 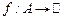 є інтегровною на множині є інтегровною на множині  і і  , то , то 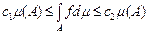 . .
Приклад 1.Якщо  , то , то 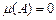 і і 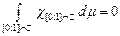 . .
5. Ознаки інтегровності функцій на множині скінченної міри.
Теорема 1. Нехай функція 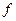 є вимірною на множині є вимірною на множині  . Тоді функції . Тоді функції 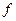 і і 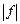 є одночасно інтегрованими на множині є одночасно інтегрованими на множині  і і
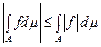 . (1) . (1)
Теорема 2. Якщо функція 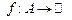 є вимірною на множині є вимірною на множині  , а функція , а функція 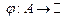 є інтегрованою на множині є інтегрованою на множині  і і
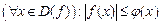 , ,
то функція 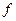 є інтегровною на є інтегровною на  і і
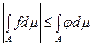 . (2) . (2)
Наслідок 1. Обмежена вимірна функція на множині скінченної міри є інтегрованою.
Приклад 1.Функція 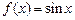 є інтегровною на будь-якій множині скінченної міри і є інтегровною на будь-якій множині скінченної міри і 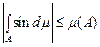 . .
Приклад 2.Нехай  – вимірна множина, – вимірна множина, 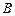 – її невимірна підмножина. Тоді функція – її невимірна підмножина. Тоді функція

є невимірною і тому не є інтегровною на  . Разом з цим, . Разом з цим, 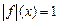 і тому функція і тому функція 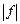 є інтегровною на є інтегровною на  . Отже, якщо функція . Отже, якщо функція 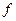 є невимірною, то функція є невимірною, то функція 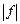 може бути інтегровною, а функція може бути інтегровною, а функція 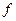 , зрозуміло, не є інтегровною (інтеграл Лебега визначається тільки для вимірних функцій). , зрозуміло, не є інтегровною (інтеграл Лебега визначається тільки для вимірних функцій).
6. Властивості інтеграла як функції множини на множині скінченної міри.
Теорема 1. Нехай  – множина скінченої міри. – множина скінченої міри.  – скінченна або зліченна множина попарно неперетинних множин скінченої міри. Тоді для кожної інтегрованої на – скінченна або зліченна множина попарно неперетинних множин скінченої міри. Тоді для кожної інтегрованої на  функції функції  виконується виконується
 , (1) , (1)
причому ряд (1) збіжний абсолютно.
Приклад 1. Нехай функція 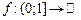 визначена формулою визначена формулою
 
Тоді 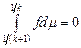 і, отже, і, отже, 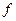 є сумовною на кожному проміжку є сумовною на кожному проміжку  . Водночас, . Водночас,
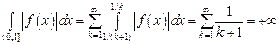 . .
Отже, 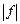 і і 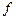 не є сумовними на не є сумовними на 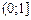 . .
Теорема 2. Якщо  – скінченна або зліченна множина попарно неперетинних вимірних множин, множина – скінченна або зліченна множина попарно неперетинних вимірних множин, множина  є множиною скінченної міри, функція є множиною скінченної міри, функція  є інтегрованою на кожній з множин є інтегрованою на кожній з множин 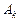 і ряд і ряд

є збіжним, то 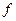 є інтегрованою на є інтегрованою на  і справедлива рівність і справедлива рівність
 . .
Приклад 2. 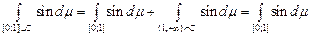 . .
Приклад 3. 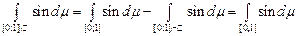 . .
Теорема 3 (нерівність М.Чебишева). Нехай функція  є вимірною та інтегрованою на множині є вимірною та інтегрованою на множині  і і 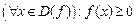 . Тоді . Тоді
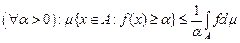 . .
Доведення. Справді, нехай 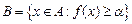 . Тоді . Тоді
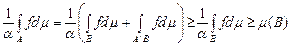 .► .►
Приклад 4. 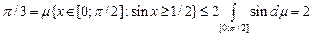 . .
Теорема 4. Якщо
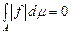 , ,
то 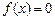 майже скрізь на майже скрізь на  . .
Доведення. Справді, для кожного 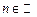
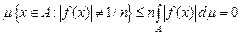 . .
Тому
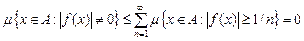 .► .►
Теорема 5 (абсолютна неперервність інтеграла). Нехай функція  єінтегрованою на множині єінтегрованою на множині  . Тоді для кожного . Тоді для кожного  знайдеться знайдеться 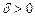 таке, що для будь-якої вимірної множини таке, що для будь-якої вимірної множини 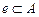 , для якої , для якої 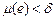 , виконується , виконується
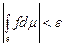 . .
Приклад 5. Якщо  , то , то 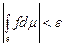 , якщо , якщо  , ,  і і 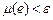 . .
7. Граничний перехід під знаком інтеграла по множині скінченної міри.
Теорема 1 (А.Лебега). Якщо послідовність 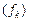 вимірних на множині вимірних на множині  функцій функцій 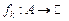 поточково на поточково на  збігається до збігається до 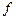 і існує сумовна на і існує сумовна на  функція функція 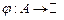 така, що така, що
 , (1) , (1)
то 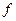 є інтегрованою на є інтегрованою на  і і
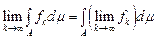 . (2) . (2)
Приклад 1. Послідовність  поточково на поточково на 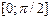 збігається до збігається до 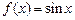 і і 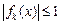 . Тому . Тому 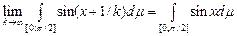 . .
Приклад 2. Якщо  –вимірна множина скінченної міри і послідовність –вимірна множина скінченної міри і послідовність 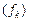 вимірних інтегровних на вимірних інтегровних на  функцій функцій 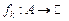 рівномірно на рівномірно на  збігається до функції збігається до функції  , то функція , то функція 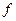 є інтегровною на є інтегровною на  і і  . Справді, з рівномірної збіжності . Справді, з рівномірної збіжності 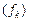 випливає, що випливає, що 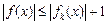 . для деякого . для деякого  і всіх і всіх 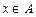 . Тому . Тому 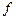 є інтегровною. Крім цього, знайдеться таке є інтегровною. Крім цього, знайдеться таке 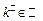 , , 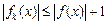 вимірних для всіх вимірних для всіх 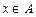 і всіх і всіх  . Залишилось скористатись теоремою Лебега. . Залишилось скористатись теоремою Лебега.
Теорема 3 (Б.Леві). Нехай 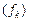 – послідовність сумовних функцій на множині – послідовність сумовних функцій на множині  скінченної міри, скінченної міри,
 , ,
і
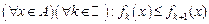 . .
Тоді майже скрізь на  існує скінченна границя існує скінченна границя  і і
 . .
Приклад 1. Послідовність  поточково на поточково на  збігається до збігається до 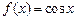 і і 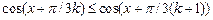 . для всіх . для всіх 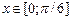 і всіх і всіх  . Тому . Тому  . .
Теорема 4 (П.Фату). Якщо  –множина скінченної міри –множина скінченної міри 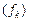 –послідовність невід’ємних сумовних функцій на множині –послідовність невід’ємних сумовних функцій на множині  , ,
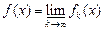 , (1) , (1)
і
 , (2) , (2)
то функція 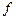 є сумовною на є сумовною на  і і
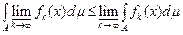 . (3) . (3)
Наслідок 1. Якщо послідовність 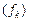 невід’ємних і сумовних на невід’ємних і сумовних на  функцій функцій 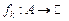 збігається майже скрізь на збігається майже скрізь на  до функції до функції  , ,
 , ,
то функція 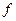 є сумовною і є сумовною і
 .► .►
Приклад 1. Послідовність  для кожного для кожного 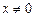 збігається до збігається до 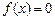 і і
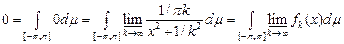  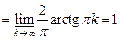 . .
Отже, в даному випадку в (3) має місце строга нерівність. Тому не можна стверджувати, що за виконання умов леми Фату
 . .
8. Інтеграл Лебега по множині нескінченної міри.Нехай  – множина нескінченної міри і така існує послідовність – множина нескінченної міри і така існує послідовність 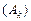 скінченної міри, для якої скінченної міри, для якої  і і  . Інтегралом Лебега невід'ємної вимірної на . Інтегралом Лебега невід'ємної вимірної на  функції функції  називається границя називається границя
 . (1) . (1)
Невід'ємної вимірна на множині  функції функції  називається інтегрованою на називається інтегрованою на  , якщо границя (1) є скінченною. Це означення є конкретним. Справді, границя (1) (скінченна або нескінченна) існує для кожної розглядуваної послідовності , якщо границя (1) є скінченною. Це означення є конкретним. Справді, границя (1) (скінченна або нескінченна) існує для кожної розглядуваної послідовності 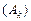 , бо числова послідовність , бо числова послідовність
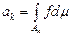
є неспадною. Крім цього, границя (1) не залежить від послідовності 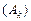 . Інтегралом вимірної на . Інтегралом вимірної на  функції функції  називається символ називається символ
 , (5) , (5)
де
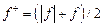 , ,  . .
Вимірна функція  називається інтегрованою на називається інтегрованою на  , якщо інтегрованою на , якщо інтегрованою на  є кожна з функцій є кожна з функцій 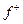 і і 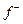 (вони невід'ємні) Використовуючи рівності (вони невід'ємні) Використовуючи рівності
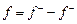 , , 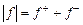 , ,
переконуємось, що всі теореми п.п. 4-8 залишаються справедливими і для інтегралів по множині  нескінченної міри. Виключення становить теорема 1 п. 4.(функція нескінченної міри. Виключення становить теорема 1 п. 4.(функція  не є інтегрованою на множині нескінченної міри). не є інтегрованою на множині нескінченної міри).
Зауваження 1. Всюди вище ми ніде не використовували, що 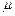 –лінійна міра на –лінійна міра на 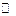 . Тому все сказане вище в даному розділі справедливе для довільної зліченно-адитивної . Тому все сказане вище в даному розділі справедливе для довільної зліченно-адитивної  -скінченної і повної міри, визначеної на довільній -скінченної і повної міри, визначеної на довільній  -алегебрі. Скзане не стосується правда розглядуваних прикладів. -алегебрі. Скзане не стосується правда розглядуваних прикладів.
10. Зв’язок між інтегралами Рімана і Лебега.
Теорема 1. Якщо функція 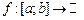 є інтегрованою за Ріманом на скінченному проміжку є інтегрованою за Ріманом на скінченному проміжку 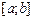 , то вона інтегрована на , то вона інтегрована на 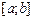 за мірою Лебега на за мірою Лебега на 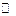 і обидва інтеграли є рівними: і обидва інтеграли є рівними:
 , ,
де 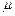 –лінійна міра Лебега на –лінійна міра Лебега на 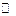 . .
Теорема 2. Для абсолютної збіжності невласного інтеграла Рімана
 (1) (1)
необхідно і достатньо, щоб функція 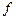 була інтегровною на була інтегровною на 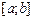 за мірою Лебега на за мірою Лебега на 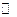 . Якщо остання умова виконана, то . Якщо остання умова виконана, то
 , (2) , (2)
де 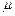 –міра Лебега на –міра Лебега на 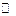 . .
Зауваження 1. Якщо 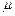 –лінійна міра Лебега на –лінійна міра Лебега на 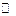 , то для позначення інтеграла Лебега , то для позначення інтеграла Лебега 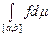 використовують також символи використовують також символи 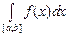 , ,  , , 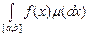 , ,  та інші. та інші.
3. Вимірний простір. Імовірнісний простір.Простором з мірою називається упорядкована трійка 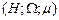 , де , де 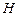 –деяка непорожня множина, –деяка непорожня множина, 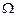 –деяка сукупність підмножин множини –деяка сукупність підмножин множини 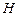 , а , а 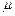 –деяка міра, для якої –деяка міра, для якої 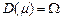 . Якщо . Якщо 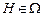 , то простір з мірою називається вимірним простором. Якщо , то простір з мірою називається вимірним простором. Якщо 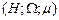 –вимірний простір, і –вимірний простір, і  , то , то 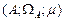 –також вимірний простір, де –також вимірний простір, де 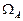 –множина тих –множина тих  , які подаються у вигляді , які подаються у вигляді 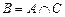 , де , де  . Міра . Міра 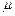 називається імовірнісною, якщо називається імовірнісною, якщо 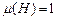 . Імовірнісним простором називається вимірний простір, в якому . Імовірнісним простором називається вимірний простір, в якому 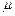 –імовірнісна міра. Імовірнісний простір лежить в основі сучасного підходу до побудови теорії імовірності. Цей підхід запропонований А.Колмогоровим. При цьому на міру накладають деякі додаткові обмеження (міра –імовірнісна міра. Імовірнісний простір лежить в основі сучасного підходу до побудови теорії імовірності. Цей підхід запропонований А.Колмогоровим. При цьому на міру накладають деякі додаткові обмеження (міра 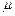 повина бути повною і зліченно- адитивною, а сукупність множин повина бути повною і зліченно- адитивною, а сукупність множин 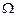 – утворювати – утворювати  -алгбру). При розгляді вимірного простору як імовірнісного змінюється термінологія: -алгбру). При розгляді вимірного простору як імовірнісного змінюється термінологія: 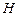 –називається простором елементарних випадкових подій, елементи простору –називається простором елементарних випадкових подій, елементи простору 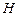 –елементарними випадковими подіями, елементи множини –елементарними випадковими подіями, елементи множини 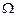 , тобто вимірні множини, –випадковими подіями ( , тобто вимірні множини, –випадковими подіями ( 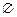 –неможлива подія, –неможлива подія, 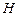 –достовірна подія), вимірна функція –достовірна подія), вимірна функція 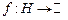 –випадкова величина, –випадкова величина,  –імовірність випадкової події –імовірність випадкової події  , послідовності , послідовності  функцій функцій  збігається майже скрізь–послідовність випадкових величин збігається з імовірністю збігається майже скрізь–послідовність випадкових величин збігається з імовірністю 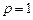 (майже напевно) і т.д. Імовірносний простір називається скінченним імовірнісним простором, якщо (майже напевно) і т.д. Імовірносний простір називається скінченним імовірнісним простором, якщо 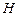 –скінченна множина і –скінченна множина і 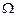 –сукупність всіх підмножин множини –сукупність всіх підмножин множини 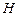 . Імовірнісний простір називається зліченним імовірнісним простором, якщо . Імовірнісний простір називається зліченним імовірнісним простором, якщо 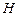 –зліченна множина і –зліченна множина і 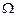 –сукупність всіх підмножин множини –сукупність всіх підмножин множини 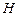 . При розгляді елементарних імовірнісних задач (кидання кубика, монети) імовірнісний простір є скінченним. . При розгляді елементарних імовірнісних задач (кидання кубика, монети) імовірнісний простір є скінченним.
Зауваження 1. Подальше узагальнення міри і інтеграла пов’язано з розглядом знакозмінних мір, зарядів тощо.
11. Запитання для самоконтролю.
1. Сформулюйте означення простої функції.
2. Сформулюйте означення інтеграла Лебега простої функції по множині скінченної міри.
3. Сформулюйте означення сумовної функції по множині скінченної міри та її інтеграла Лебега.
4. Сформулюйте означення сумовної функції по множині нескінченної міри та її інтеграла Лебега.
5. Сформулюйте і доведіть теорему про умови вимірності простої функції.
6. Сформулюйте і доведіть теорему про умови вимірності функції в термінах простих функції.
7. Сформулюйте про адитивну властивість інтеграла простої функції як функції проміжку.
8. Сформулюйте і доведіть теореми про коректність означення інтеграла Лебега по множині скінченної міри.
10. Сформулюйте теореми про властивості інтеграла Лебега як функції проміжку і доведіть одну з них.
11. Сформулюйте і доведіть теорему про нерівність Чебешова.
12. Сформулюйте теорему про абсолютну неперервність інтеграла Лебега.
14. Сформулюйте теорему Лебега про граничний перехід зв інтегралі.
15. Сформулюйте і доведіть теорему Леві про граничний перехід зв інтегралі.
16. Сформулюйте і доведіть теорему(лему) Фату про граничний перехід в інтегралі.
17. Сформулюйте теорему про взаємозв’язок між інтегралами Лебега та Рімана.
Вправи та задачі.
1.З’ясуйте, чи функція 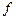 є інтегровною за Лебегом на множині є інтегровною за Лебегом на множині 
1. 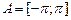 , , 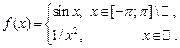
2. 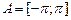 , , 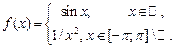
3.  , , 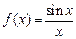 . .
4. 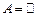 , , 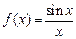 . .
5. 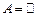 , ,  . .
6. 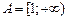 , , 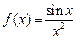 . .
7.  , , 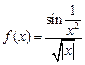 . .
8. 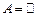 , , 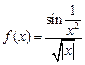 . .
9. 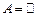 , , 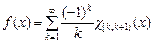 . .
10.  , , 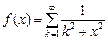 . .
11. 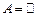 , ,  . .
12. 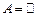 , , 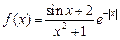 . .
13. 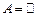 , , 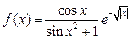 . .
14.  , ,  . .
15.  , ,  . .
16.  , , 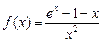 . .
17. 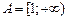 , , 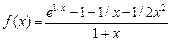 . .
18. 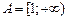 , , 
19.  , , 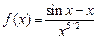 . .
20.  , , 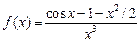 . .
21.  , , 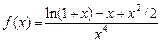 . .
22. 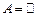 , , 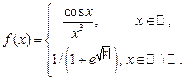
23. 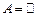 , , 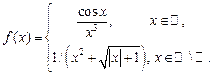
24.  , ,  . .
25. 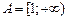 , ,  . .
26.  , , 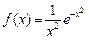 . .
27.  , , 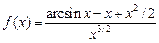 . .
28. 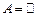 , , 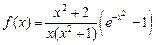 . .
29. 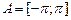 , , 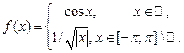
30. 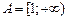 , ,  . .
31. 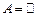 , , 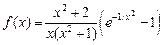 . .
2.Знайдіть інтеграл 
1. 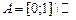 , ,  . .
2. 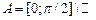 , , 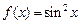 . .
3. 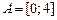 , , 
4. 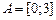 , , 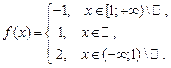
5. 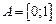 , , 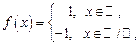
6. 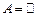 , , 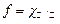
7. 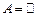 , , 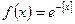
8.  , , 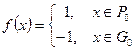
9.  , ,  
10.  , , 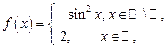 
11.  , , 
12. 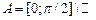 , , 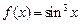 . .
13.  , , 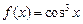 . .
14. 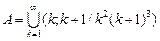 , , 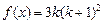 для для 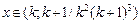 . .
15. 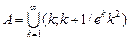 , , 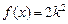 для для  . .
16.  , , 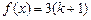 для для 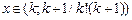 . .
17.  , ,  . .
18. 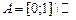 , ,  . .
19.  , , 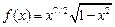 . .
20. 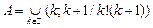 , , 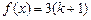 для для 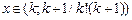 . .
21. 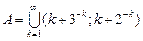 , , 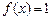 для для ![]()
Поиск по сайту:
|

 визначається як границя інтегральних сум:
визначається як границя інтегральних сум: 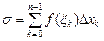 , де
, де 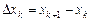 ,
, 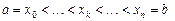 і
і 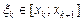 . Проте, ряд достатньо простих функцій не є інтегровними за Ріманом. До таких належать, зокрема, функція
. Проте, ряд достатньо простих функцій не є інтегровними за Ріманом. До таких належать, зокрема, функція 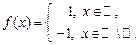 Інтеграл Лебега є узагальненим інтегралом Рімана. Основна ідея побудови інтеграла Лебега полягає в тому, що
Інтеграл Лебега є узагальненим інтегралом Рімана. Основна ідея побудови інтеграла Лебега полягає в тому, що  множиться не на
множиться не на  , а на міру множини тих
, а на міру множини тих 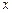 , в яких функція
, в яких функція 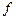 приймає значення близькі до
приймає значення близькі до  , якщо
, якщо 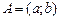 і
і 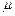 –лінійна міра Лебега на
–лінійна міра Лебега на 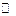 . Відповідні не змінюються суттєво, якщо
. Відповідні не змінюються суттєво, якщо  –довільна вимірна множина і
–довільна вимірна множина і  -скінченна міра.
-скінченна міра. на
на 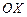 . Наприклад, функція
. Наприклад, функція 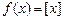 є простою.
є простою.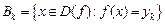 були вимірними.
були вимірними.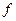 – вимірна функція. Оскільки
– вимірна функція. Оскільки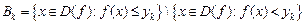 ,
,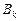 мусить бути вимірною. Нехай усі множини
мусить бути вимірною. Нехай усі множини 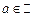 множина
множина 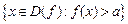 є об’єднанням скінченної або зліченної кількості множин
є об’єднанням скінченної або зліченної кількості множин  і існувала послідовність
і існувала послідовність 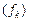 простих вимірних на
простих вимірних на 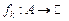 , яка рівномірно на
, яка рівномірно на  збігається до
збігається до  , якщо
, якщо  , де
, де 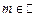 і
і 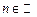 . Тоді
. Тоді  ,
, 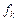 – прості вимірні функції,
– прості вимірні функції, 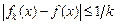 для всіх
для всіх  і
і  рівномірно на
рівномірно на 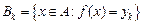 . Інтегралом Лебега простої функції
. Інтегралом Лебега простої функції 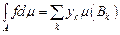 . (1)
. (1) – сукупність скінченної або зліченної кількості вимірних попарно неперетинних множин,
– сукупність скінченної або зліченної кількості вимірних попарно неперетинних множин, 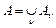 –множина скінченої міри, то для кожної простої функції
–множина скінченої міри, то для кожної простої функції 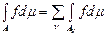 (2)
(2)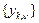 – множина значень функції
– множина значень функції 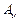 ,
, 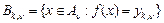 . Тоді
. Тоді .
.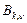 попарно неперетинні,
попарно неперетинні, 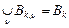 і
і  ,
,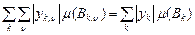 ,
, 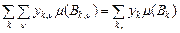 .
.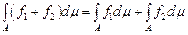 , якщо останні два інтеграли існують.
, якщо останні два інтеграли існують.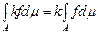 для будь-якої числової сталої
для будь-якої числової сталої 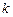 , якщо останній інтеграл існує.
, якщо останній інтеграл існує. для будь-яких чисел
для будь-яких чисел  і
і  , якщо останні інтеграли існують.
, якщо останні інтеграли існують. .
.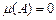 , то
, то .
. для будь-якої вимірної множини
для будь-якої вимірної множини 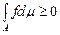 .
.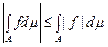 .
.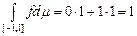 , якщо
, якщо 
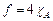 ,
, 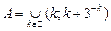 , то функція
, то функція  ,
, 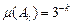 ,
, 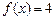 для
для 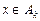 і
і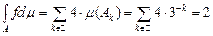 .
. (1)
(1) . Тоді
. Тоді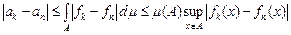 . ( 2)
. ( 2) – нормою на
– нормою на  . Отже, границя (1) існує. ►
. Отже, границя (1) існує. ► – дві рівномірно збіжні до
– дві рівномірно збіжні до 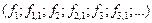 (3)
(3) .►
.►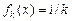 для
для 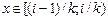 , то функції є простими на множині
, то функції є простими на множині  і послідовність
і послідовність 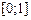 збігається до функції
збігається до функції 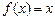 . При цьому,
. При цьому, 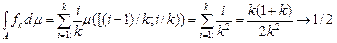 .
. .
.  є простою. ►
є простою. ► виконується
виконується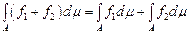 ,
,
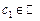 і
і 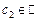
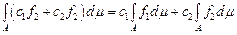 ,
,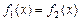 майже скрізь на
майже скрізь на 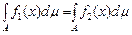 ,
, , то
, то 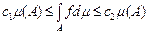 .
. , то
, то 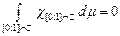 .
.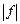 є одночасно інтегрованими на множині
є одночасно інтегрованими на множині 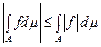 . (1)
. (1)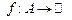 є вимірною на множині
є вимірною на множині 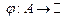 є інтегрованою на множині
є інтегрованою на множині 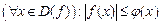 ,
,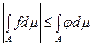 . (2)
. (2)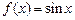 є інтегровною на будь-якій множині скінченної міри і
є інтегровною на будь-якій множині скінченної міри і 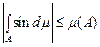 .
.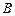 – її невимірна підмножина. Тоді функція
– її невимірна підмножина. Тоді функція
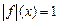 і тому функція
і тому функція  – множина скінченої міри.
– множина скінченої міри.  – скінченна або зліченна множина попарно неперетинних множин скінченої міри. Тоді для кожної інтегрованої на
– скінченна або зліченна множина попарно неперетинних множин скінченої міри. Тоді для кожної інтегрованої на  , (1)
, (1)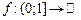 визначена формулою
визначена формулою

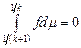 і, отже,
і, отже,  . Водночас,
. Водночас,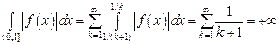 .
. .
.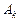 і ряд
і ряд
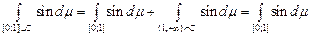 .
.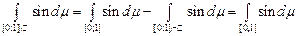 .
.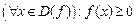 . Тоді
. Тоді 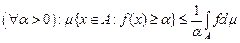 .
.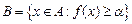 . Тоді
. Тоді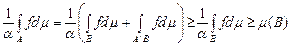 .►
.►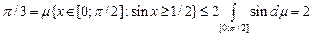 .
.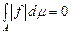 ,
, майже скрізь на
майже скрізь на 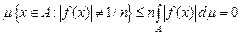 .
.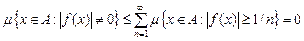 .►
.► знайдеться
знайдеться 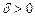 таке, що для будь-якої вимірної множини
таке, що для будь-якої вимірної множини 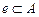 , для якої
, для якої 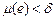 , виконується
, виконується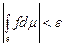 .
. , то
, то  і
і 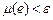 .
. 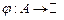 така, що
така, що , (1)
, (1)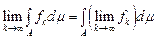 . (2)
. (2) поточково на
поточково на 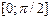 збігається до
збігається до 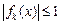 . Тому
. Тому 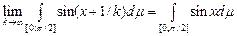 .
.  . Справді, з рівномірної збіжності
. Справді, з рівномірної збіжності 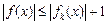 . для деякого
. для деякого 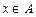 . Тому
. Тому 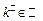 ,
, 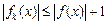 вимірних для всіх
вимірних для всіх  . Залишилось скористатись теоремою Лебега.
. Залишилось скористатись теоремою Лебега. ,
, 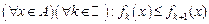 .
. і
і .
. поточково на
поточково на  збігається до
збігається до 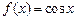 і
і 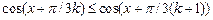 . для всіх
. для всіх 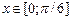 і всіх
і всіх  .
. 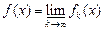 , (1)
, (1)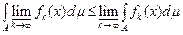 . (3)
. (3) ,
,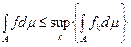 .►
.► для кожного
для кожного  збігається до
збігається до 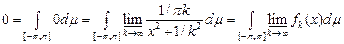

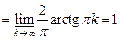 .
. .
. скінченної міри, для якої
скінченної міри, для якої  і
і  . (1)
. (1)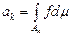
 , (5)
, (5)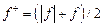 ,
,  .
.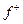 і
і 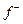 (вони невід'ємні) Використовуючи рівності
(вони невід'ємні) Використовуючи рівності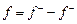 ,
, 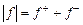 ,
,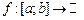 є інтегрованою за Ріманом на скінченному проміжку
є інтегрованою за Ріманом на скінченному проміжку 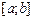 , то вона інтегрована на
, то вона інтегрована на  ,
,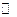 . Якщо остання умова виконана, то
. Якщо остання умова виконана, то  , (2)
, (2)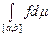 використовують також символи
використовують також символи 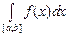 ,
, 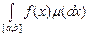 ,
,  та інші.
та інші.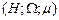 , де
, де 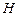 –деяка непорожня множина,
–деяка непорожня множина, 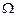 –деяка сукупність підмножин множини
–деяка сукупність підмножин множини 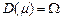 . Якщо
. Якщо 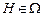 , то простір з мірою називається вимірним простором. Якщо
, то простір з мірою називається вимірним простором. Якщо  , то
, то 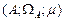 –також вимірний простір, де
–також вимірний простір, де 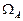 –множина тих
–множина тих  , які подаються у вигляді
, які подаються у вигляді 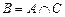 , де
, де  . Міра
. Міра 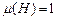 . Імовірнісним простором називається вимірний простір, в якому
. Імовірнісним простором називається вимірний простір, в якому 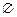 –неможлива подія,
–неможлива подія, 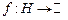 –випадкова величина,
–випадкова величина,  –імовірність випадкової події
–імовірність випадкової події  , послідовності
, послідовності  функцій
функцій  збігається майже скрізь–послідовність випадкових величин збігається з імовірністю
збігається майже скрізь–послідовність випадкових величин збігається з імовірністю 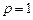 (майже напевно) і т.д. Імовірносний простір називається скінченним імовірнісним простором, якщо
(майже напевно) і т.д. Імовірносний простір називається скінченним імовірнісним простором, якщо 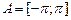 ,
, 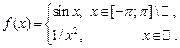
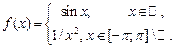
 ,
, 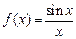 .
.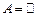 ,
,  .
.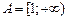 ,
, 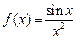 .
.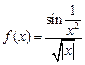 .
. .
. .
. .
.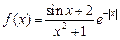 .
.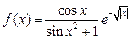 .
. .
. .
.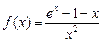 .
.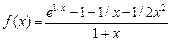 .
.
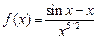 .
.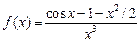 .
.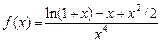 .
.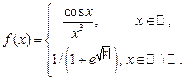
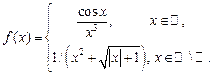
 .
.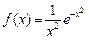 .
.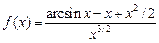 .
.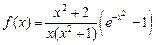 .
.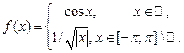
 .
.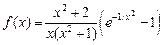 .
.
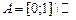 ,
,  .
.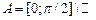 ,
, 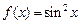 .
.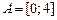 ,
, 
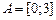 ,
, 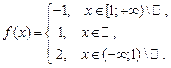
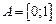 ,
, 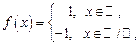
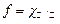
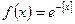
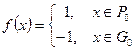
 ,
, 

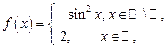

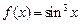 .
. ,
, 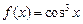 .
.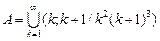 ,
, 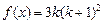 для
для 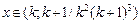 .
.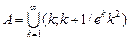 ,
, 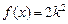 для
для  .
. ,
, 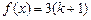 для
для 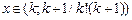 .
. ,
,  .
. .
.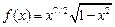 .
.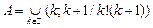 ,
, 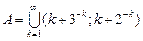 ,
, 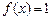 для
для