 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Порядок виконання вимірювань
Порядок виконання роботи Завдання 1. Перевірка закона руху. З (5.3 − 5.5) випливає, що обертання маятника Обербека відбувається з постійним кутовим прискоренням
Використовуючи (5.9), визначимо час Dt проходження вантажу між позначками x1 та x2:
З (5.10) випливає, що у випадку рівноприскореного руху (a = const) і при фіксованих положеннях х0 і х2 залежність часу Dt від
Порядок виконання вимірювань 1. Встановити вантажі m0 в середнє положення, размістивши їх на рівних відстанях від осі таким чином, щоб маятник знаходився в положені байдужої рівноваги. В цьому стані маятник, приведений в обертальний рух, зупиняється щоразу в новому положенні, і його зупинка не супроводжується коливаннями навколо положення рівноваги. Рух вантажа m завжди починається з одного й того ж положення х0, яке необхідно записати в протокол. Нитку намотують на вал шківа більшого діаметра виток до витка. 2. Відпустити вантаж m та виміряти час Dt , проходження між позначками х1 та х2. Дані записати до табл. 5.1. Провести вимірювання часу Dt для 5 положень х1 верхнього датчика (рекомендується змінювати х1 з кроком 3 см). Для кожного положення датчика вимірювання часу провести не менше n = 3 разів. 3. Для 5−7-ми перших дослідів виміряти значення х4 − позначки, до якої піднимається вантаж при обертанні маятника в один бік. Результати занести до табл. 5.1. 4. Визначити значення х3 − максимальної позначки, до якої опускається вантаж m під час руху. Обробка результатів 1. За експериментальними даними для кожного положення фотоприймача х1 розрахувати середнє значення Dt за формулою
де n − кількість вимірювань при кожному фіксованому положенні х1. Результати обчислень занести до табл. 5.1. 2. Побудувати залежність 3. Знайти середнє значення 4. Визначити лінійне прискорення вантажа а та кутове прискорення шківа β:
5. Розрахувати середнє значення лінійного прискорення <a> і середнє значення кутового прискорення <β>. Результати обчислень занести до табл. 5.1. Положення кронштейнів: x0 = . м, x2 = . м. Максимальна позначка, до якої опускається вантаж m: х3 = . м. Таблиця 5.1.
Завдання 2. Експериментальна перевірка незалежності інерційних властивостей маятника (моменту інерції) від моменту зовнішніх сил. З рівняння (5.3) маємо
Із рівнянь (5.6), (5.10) випливає, що
Всі величини, що входять до рівняння (5.11), крім відомих m і g, визначаються експериментально. Порядок проведення вимірювань: 1. Виміряти штангенциркулем радіуси R1 і R2 шківів результати занести до протоколу. 2. Встановити максимальну відстань між кронштейнами. Записати до протоколу координати положення кронштейнів х1, х2 і значення х0. 3. Встановити вантажі m0 в середнє положення, розмістивши їх на однакових відстанях від осі таким чином, щоб маятник знаходився в стані байдужої рівноваги. 4. До кінця нитки, яка намотана на шків радіуса R1, прикріпити вантаж масою m1 та виміряти час Dt проходження вантажу між кронштейнами х1 і х2. Одночасно виміряти позначку, до якої підніметься вантаж х4. Вимірювання провести 3 рази і результати занести до таблиці 5.2. 5. Перекинути нитку на інший шків (радіуса R2) та виміряти час Dt і значення х4 (3 рази). Результати занести до таблиці 5.2. 6. Провести вимірювання, подібні до п.4−п.5, закріпивши до кінця нитки вантаж масою m2. Результати вимірювань занести до табл.5.2.
R1 = . м; R2 = . м; m1= . кг; m2= . кг; х1 = . м; х2 = . м; х0 = . м; х3 = . м. Таблиця 5.2.
Обробка результатів 1. Обчислити значення моментів інерції маятника 2. Визначити значення < х4> для кожного досліду, і оцінити відношення 3. Результати обчислень занести до табл. 5.2. Завдання.3. Перевірка основного рівняння обертального руху і теореми Гюйгенса–Штейнера. Момент інерції тіла залежить від матеріалу, форми і розмірів тіла, а також від розташування відносно осі обертання. Розрахунок моменту інерції тіла відносно осі, що не проходить через центр мас, виконується за допомогою теореми Штейнера: момент інерції тіла відносно довільної осі Z дорівнює сумі моменту інерції I0 тіла відносно паралельної їй осі, яка проходить через центр мас тіла, і добутку маси тіла m на квадрат відстані між цими осями. Нехай I0' – сумарний момент інерції чотирьох вантажів з масами m0 відносно осі, яка проходить через їх центр мас. При віддаленні центрів вантажів на відстань
Якщо
При віддаленні центрів мас вантажів на відстань
Враховуючи рівняння (5.6) і (5.10) залежність квадрата часу проходження вантажем між позначками
Якщо
Рівняння (5.15) і (5.16) дають
де
Порядок виконання вимірювань
1. До кінця нитки намотаної на шків радіуса R2 (більшого за розміром), закріпити вантаж найбільшої маси. 2. Встановити мінімальне значення моменту інерції маятника. Для цього чотири вантажі масою m0 встановлюють якнайближче до осі. Виміряти відстань 3. Визначити величину 4. Змінюючи положення вантажів m0 на стрижнях симетрично з кроком 3 см, кожний раз вимірюють час
Таблиця 5.3
Обробка результатів 1. За експериментальними даними для кожного положення вантажів m0 знайти середнє значення 2. Побудувати графік залежності квадрату часу опускання вантажу 3. Перевірити співвідношення (5.17) для кількох пар значень 4. Для кожного момента інерції (тобто для кожного положення вантажів m0) визначити
Оформлення звіту з лабораторної роботи завершується розрахунком похибок отриманих величин і написанням висновків.
Контрольні запитання 1. Що називається кутовою швидкістю і кутовим прискоренням? 2. Як визначається напрямок вектора кутової швидкості, кутового прискорення? 3. Що таке момент сили відносно деякої точки? Куди він спрямований? 4. Що таке момент сили відносно закріпленої осі? 5. Що таке момент інерції тіла відносно закріпленої осі? Від чого залежить момент інерції і який його вплив на обертальний рух? 6. Сформулюйте та доведіть теорему Гюйгенса – Штейнера. 7. Отримайте рівняння моментів і основне рівняння обертального руху відносно закріпленої осі.
Література 1. Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1980, §31, 32, 34. 2. Сивухин Д.В. Общий курс физики. Том 1. Механика, 3-е изд. М.: Наука. 1989. §30, 3 3. Деденко Л.Г., Керженцев В.В. Математическая обработка результатов экспериментов в лабораториях общего физического практикума. М.: Изд-во Моск. ун-та, 1977.
Поиск по сайту: |
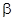 , при цьому вантаж m опускається з постійним лінійним прискоренням а. Координата х змінюється за законом (вісь х системи координат спрямовано донизу):
, при цьому вантаж m опускається з постійним лінійним прискоренням а. Координата х змінюється за законом (вісь х системи координат спрямовано донизу):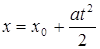 (5.9)
(5.9) (5.10)
(5.10) носить лінійний характер і зображується на графіку прямою лінією.
носить лінійний характер і зображується на графіку прямою лінією.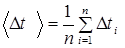 ,
, від
від  , та переконатися в тому, що рух вантажа рівноприскорений.
, та переконатися в тому, що рух вантажа рівноприскорений. та оцінити величину
та оцінити величину  за формулою (5.8). Переконатися в малому значенні момента сили тертя порівняно з початковим моментом сили тяжіння mgR.
за формулою (5.8). Переконатися в малому значенні момента сили тертя порівняно з початковим моментом сили тяжіння mgR.
 .
. , м
, м
 , с
, с

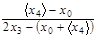
 , м/с2
, м/с2
 , с-2
, с-2

 (5.11)
(5.11)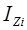 , кг·м2
, кг·м2
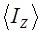 , кг·м2
, кг·м2

 за формулою (5.11), а також середнє значення моменту інерції <
за формулою (5.11), а також середнє значення моменту інерції < 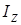 > для кожного досліду.
> для кожного досліду. , від осі обертання, згідно з теоремою Гюйгенса–Штейнера, момент інерції цих вантажів дорівнюватиме
, від осі обертання, згідно з теоремою Гюйгенса–Штейнера, момент інерції цих вантажів дорівнюватиме  :
: . (5.12)
. (5.12) – момент інерції маятника без вантажів, то загальний момент інерції маятника буде дорівнювати:
– момент інерції маятника без вантажів, то загальний момент інерції маятника буде дорівнювати: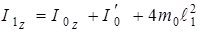 . (5.13)
. (5.13) маємо:
маємо: . (5.14)
. (5.14) і
і  від відстані
від відстані 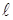 між центром вантажу m0 і віссю обертання має вигляд:
між центром вантажу m0 і віссю обертання має вигляд: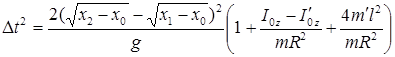 (5.15)
(5.15) , то
, то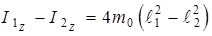 . (5.16)
. (5.16) , (5.17)
, (5.17) і
і  – час проходження вантажу між датчиками для випадку
– час проходження вантажу між датчиками для випадку  і
і 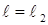 відповідно. Рівняння (5.17) містить величини, які визначаються експериментально.
відповідно. Рівняння (5.17) містить величини, які визначаються експериментально. , – час проходження вантажа m між двома кронштейнами і x4 – відмітку, до якої він піднімається в процесі руху. Вимірювання проводять 3 рази. Результати занести в табл. 5.3.
, – час проходження вантажа m між двома кронштейнами і x4 – відмітку, до якої він піднімається в процесі руху. Вимірювання проводять 3 рази. Результати занести в табл. 5.3. , с
, с
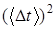 , с2
, с2
 , см2
, см2
 , см
, см

 .
. і оцінити згідно (5.8) відношення
і оцінити згідно (5.8) відношення 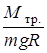 . Переконатися у виконанні наближення
. Переконатися у виконанні наближення  .
.