|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Изгиб прямоугольной плиты
Казанский государственный архитектурно-строительный университет
Кафедра Сопротивления материалов и основ теории упругости
Изгиб прямоугольной плиты Методические указания для выполнения расчетно-графической работы «Изгиб плиты» студентами специальностей: 270205 Автомобильные дороги и аэродромы 270201 Мосты и транспортные тоннели
Казань Составитель: к.ф.-м.н., доцент Нефедов В.И.
УДК 539.3 ББК 22.251
Методические указания по выполнению расчетно-графической работы для студентов специальностей 270205, 270201 / Каз.гос. арх.-строит. университет; Состав.: Нефедов В.И. Казань, 2008. 7 с.
Приводятся постановка задачи и формулы для вычисления внутренних силовых факторов и напряжений в шарнирно опертой по контуру прямоугольной плите под действием на нее равномерно распределенной нагрузки. Приведен пример составления алгоритма вычислений.
Рецензент: к.ф.-м.н., доцент кафедры «Сопротивления материалов» КГТУ им.А.Н.Туполева Луканкин С.А.
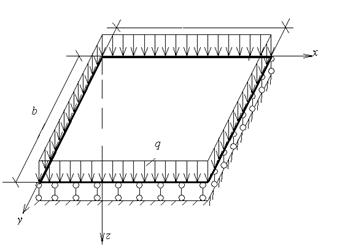
ÓКазанский государственный архитектурно-строительный университет, 2008. Рассматривается задача об изгибе шарнирно опертой по контуру прямоугольной плиты (пластинки) под действием равномерно распределенной нагрузки
Рис.1 | Геометрические (  толщина плиты), физические (модуль продольной упругости Е и коэффициент Пуассона толщина плиты), физические (модуль продольной упругости Е и коэффициент Пуассона  ) и силовой ) и силовой  параметры выбира-ются по индивидуальному шиф-ру.
Требуется определить функ-цию прогибов плиты параметры выбира-ются по индивидуальному шиф-ру.
Требуется определить функ-цию прогибов плиты  и выражающиеся через нее внут-ренние силовые факторы: и выражающиеся через нее внут-ренние силовые факторы: 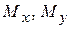 (погонные изгибающие (погонные изгибающие
|
моменты),  (погонные перезывающие силы),
(погонные перезывающие силы), 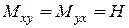 (погонный крутящий момент), а также реакции в углах плиты и погонные реакции на контуре. Также необходимо построить эпюры нормальных
(погонный крутящий момент), а также реакции в углах плиты и погонные реакции на контуре. Также необходимо построить эпюры нормальных 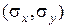 и касательных
и касательных  напряжений в поперечных сечениях плиты, в которых соответствующие внутренние силовые факторы не равны нулю; определить максимальные напряжения и при заданном значении
напряжений в поперечных сечениях плиты, в которых соответствующие внутренние силовые факторы не равны нулю; определить максимальные напряжения и при заданном значении  проверить условия прочности.
проверить условия прочности.
Задача решается методом Навье. Искомая функция прогибов  должна удовлетворять дифференциальному уравнению изгиба плиты
должна удовлетворять дифференциальному уравнению изгиба плиты
 (1)
(1)
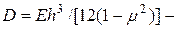 цилиндрическая жесткость плиты, и граничным условиям на контуре, где прогибы и изгибающие моменты равны нулю:
цилиндрическая жесткость плиты, и граничным условиям на контуре, где прогибы и изгибающие моменты равны нулю:
при  (2)
(2)
при  (3)
(3)
Уравнению (1) и условиям (2), (3) удовлетворяет функция
 (4)
(4)
где 
 (5)
(5)
С использованием (4), внутренние (погонные) силовые факторы определяются в виде (следует ограничиться членами ряда (4), для которых  ):
):
 (6)
(6)
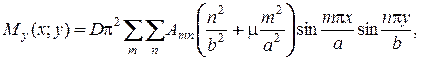 (7)
(7)
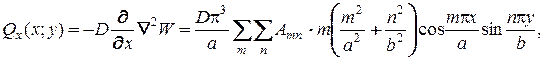 (8)
(8)
 (9)
(9)
 (10)
(10)
В (8), (9) 
Предварительно, целесообразно составить таблицу коэффициентов 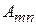 (5), используя которую можно вычислить и коэффициенты рядов (6)-(10).
(5), используя которую можно вычислить и коэффициенты рядов (6)-(10).
В рассматриваемой задаче плоскости  в системе координат
в системе координат  (рис.1) являются плоскостями всех трех видов симметрии: геометрической, физической и силовой. Поэтому напряженно-деформированное состояние плиты должно быть симметричным относительно этих плоскостей. Данному требованию удовлетворяют лишь функции (4), (6), (7), тогда как (8)-(10) являются кососимметричными.
(рис.1) являются плоскостями всех трех видов симметрии: геометрической, физической и силовой. Поэтому напряженно-деформированное состояние плиты должно быть симметричным относительно этих плоскостей. Данному требованию удовлетворяют лишь функции (4), (6), (7), тогда как (8)-(10) являются кососимметричными.
С учетом симметрии функций (4), (6), (7) и кососимметрии (8)-(10), их можно определить лишь в прямоугольной области  , вычисляя значения функций в узловых точках (рис.2)
, вычисляя значения функций в узловых точках (рис.2)
 (11)
(11)
 (12)
(12)
При этом натуральные числа  и
и  задаются в зависимости от требуемой точности построения соответствующих графиков-функций.
задаются в зависимости от требуемой точности построения соответствующих графиков-функций.
Формулы (4), (6)-(10), после подстановки в них (11), (12), изменятся очевидным образом.

 Рис.2 Рис.2
| На практике, как правило, достаточно знать лишь наиболь-шие значения функций (4), (6)-(10), которые и используются при расчетах на прочность и жесткость. В этом случае необходимо определить лишь  , ,  , , 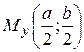 , ,  , ,  , ,  . .
|
Так, например, 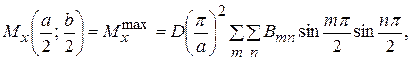 (13)
(13)
где 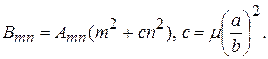
В развернутом виде (13) запишется так:
 (14)
(14)
Выражения, аналогичные (14), легко составить и для функций (4), (7)-(10).
Для построения эпюр прогибов и внутренних силовых факторов, необходимо вычислить промежуточные (между нулевым и максимальным) значения функций: 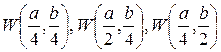 и, в тех же точках,
и, в тех же точках,  , а также
, а также 

Рассмотрим угловые и погонные опорные реакции в плите (рис.3)
| |||
| |||

Рис.3 |  (15) (15)
 (16) (16)
 (17)
После подстановки в (16), (17) функ- ции (4), выражения (17)
После подстановки в (16), (17) функ- ции (4), выражения  приобре-тают тот же вид, что и (8), (9). приобре-тают тот же вид, что и (8), (9).
|
Нормальные и касательные напряжения определяются в виде:


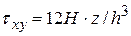
С использованием этих зависимостей, строятся эпюры напряжений в указанных выше поперечных сечениях плиты.
Проверить прочность плиты по наибольшим напряжениям  :
:
 в точках, наиболее удаленных от срединной плоскости, т.е. при
в точках, наиболее удаленных от срединной плоскости, т.е. при 
(принять 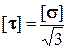 ).
).
По указанию преподавателя, студент должен проверить некоторые результаты вычислений (например, значение 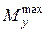 ), сопоставив их с результатами, полученными с использованием составленной на кафедре компьютерной программы «PLITA». При вычислении прогибов, внутренних силовых факторов и реакций, с использованием ЭВМ – по аналогии с формулами (11), (12) – следует задать шаг сетки Dх, Dу:
), сопоставив их с результатами, полученными с использованием составленной на кафедре компьютерной программы «PLITA». При вычислении прогибов, внутренних силовых факторов и реакций, с использованием ЭВМ – по аналогии с формулами (11), (12) – следует задать шаг сетки Dх, Dу:  (N, K – натуральные числа).
(N, K – натуральные числа).
Литература
1.Терегулов И.Г. Сопротивление материалов и основы теории упругости и пластичности. - М.: Высшая школа, 1984. С.363-400.
2.Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. - М.: Высшая школа, 1990. С.146-174.
3.Самуль В.И. Основы теории упругости и пластичности. - М.: Высшая школа, 1982. С.116-134.
изгиб прямоугольной плиты
Поиск по сайту:
 (рис.1).
(рис.1).