|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Кінетика біологічних процесів
1. Особливості кінетики біологічних процесів. 2. Константа швидкості реакції. Енергія активації. 3. Вплив температури на швидкість реакції в біологічних системах. 4. Кінетика ензиматичних процесів. Рівноважна кінетика Міхаеліса-Ментен. 5. Стаціонарна кінетика Бріггса-Холдейна. 6. Кінетика інгібування ензиматичних реакцій.
1. Усі біологічні процеси проходять і розвиваються в часі. Важливою кількісною характеристикою для опису часових процесів є швидкість процесу або швидкість реакції. Кінетика вивчає швидкість реакцій та їх залежність від різних факторів (температури, тиску, рН, концентрації речовин, активаторів, інгібіторів тощо). У живій клітині водночас відбувається величезна кількість хімічних реакцій, у ході яких розщеплюються молекули, перетворюється та нагромаджується енергія хімічних зв’язків, синтезуються низькомолекулярні сполуки, макромолекули та надмолекулярні комплекси. Для хімічної взаємодії молекул (здійснення хімічної реакції) необхідне їх зіткнення. Кінетична енергія таких зіткнень використовується для послаблення чи розриву хімічних зв’язків у молекулах реагентів. У результаті теплового руху відбувається багато зіткнень, але лише деякі з них призводять до хімічного перетворення. Необхідна умова ефективного зіткнення, яке закінчується хімічним перетворенням, – достатній запас внутрішньої вільної енергії (G) молекул у момент зіштовхування. Перебіг хімічної реакції визначається величиною зміни вільної енергії ∆G, яка є різницею між значеннями внутрішніх вільних енергій молекул продукту та вихідних речовин. Якщо вільна енергія у вихідних речовин вища, ніж у продуктів (∆G негативне), то можливе самовільне протікання реакції (екзергонічна реакція). Якщо навпаки (∆G позитивне) – самовільний перебіг реакції неможливий (реакція ендергонічна). Варто розрізняти поняття зміни вільної енергії ∆G і зміни стандартної вільної енергії ∆G°. Величина ∆G чисельно дорівнює величині ∆G° лише у випадку 1М концентрації вихідних речовин і продуктів реакції та стандартних умов проходження реакції. Отже, якщо за позитивного значення величини ∆G реакція термодинамічно неможлива, то при ∆G°>0 реакція все ж може відбуватись за умови такого співвідношення концентрацій вихідних речовин і продуктів, при якому ∆G буде негативним. Відрізнятися такі реакції будуть напрямком перебігу. Так, якщо ∆G°<0, рівновага хімічної реакції буде зсунута в бік прямої реакції (праворуч відповідно до рівняння реакції), якщо ∆G°>0 – у бік зворотної реакції. 2. Для перетворення в продукт реагент повинен подолати найвищу точку енергетичної кривої (енергетичний бар’єр), вільна енергія якої (Gа) вища за значення G реагенту. Різниця між цими величинами є енергією активації (Еа). Отже, енергією активації називається кількість енергії, яка необхідна для переводу при даній температурі усіх молекул одного моля речовини в активований стан. Чим вища енергія активації, тим повільніше іде хімічна реакція. Для кожної хімічної реакції існує перехідний стан, який характеризується високою вільною енергією і визначається як стан взаємодіючих молекул, який відповідає вершині енергетичного активаційного бар’єра. Зауважимо, що внутрішня вільна енергія G є середнім значенням енергії для молекул. Однак вона постійно змінюється через тепловий рух, коливається біля середньої величини. За певних умов (наприклад, під час зіткнення з іншими молекулами) енергія може перевищити енергію активації, в результаті чого молекула реагенту подолає енергетичний бар’єр і перетвориться в продукт. Енергія, яку треба витратити для „підйому” вільної енергії молекули від середнього значення G до максимального Gа повністю компенсується при самостійному „скочуванні” значення вільної енергії молекули вниз до енергетичного рівня продуктів реакції.
Швидкість більшості хімічних реакцій пропорційна концентрації реагентів у системі. Так, якщо в гомогенній системі відбувається реакція А + В → Р, то швидкість такої реакції, згідно з хімічною кінетикою, – це зміна концентрації одного з вихідних або кінцевих продуктів А, В, Р, віднесена до одиниці часу t:
Обчислюючи зміни концентрації вихідних речовин за певний проміжок часу, неможливо визначити істинну швидкість реакції, оскільки вона постійно змінюється. Отже, для визначення швидкості в даний момент часу необхідно знайти D[A] або D[B] за малий проміжок часу в границі, що наближається до нуля (Dt→0). Границею такої функції є похідна від концентрації по часу:
Згідно з основним законом кінетики (законом діючих мас) швидкість реакції за постійної температури пропорційна добутку концентрацій реагуючих речовин, узятих в степенях, які дорівнюють стехіометричним коефіцієнтам. Так, для реакції αА + βВ → γР швидкість розраховується в такий спосіб:
де коефіцієнт пропорційності k – це константа швидкості реакції (швидкість реакції при концентраціях реагуючих речовин, що дорівнюють 1). Реакції класифікують за багатьма ознаками, але в першу чергу за молекулярністю і загальним (сумарним) порядком. Молекулярність реакції має безпосереднє відношення до механізму реакції та характеризується числом молекул, які беруть участь у елементарному акті хімічного перетворення. Молекулярність реакції може набувати лише цілочисельних значень, тобто реакції можуть бути моно-, бі- та тримолекулярні. Реакції більшої молекулярності практично не зустрічаються, тому що ймовірність одночасного зіткнення чотирьох або більшої кількості молекул надзвичайно мала. Порядок реакціївизначають за більш формальною ознакою, ніж її молекулярність, а саме за видом рівняння, яке передає залежність швидкості реакції від концентрації реагуючих речовин. Загальний порядок реакції дорівнює сумі показників ступенів, в яких концентрації всіх початкових речовин входять у кінетичне рівняння Реакції можуть бути нульового, 1-го, 2-го, 3-го та інших порядків. У простому хімічному перетворенні, коли А→Р, швидкість реакції суворо пропорційна концентрації однієї реагуючої речовини
Це реакція першого порядку. Знак мінус свідчить про витрату речовини. Для знаходження сталих швидкостей реакцій, це диференціальне рівняння інтегрують. Для цього розподіляють у ньому змінні таким чином:
Нехай у початковий момент часу t=0концентрація речовини А становить [A]0. Після початку реакції відбувається витрата речовини А і на момент часу t вона досягає [A]. Проінтегрувавши рівняння, одержуємо: [A]=[A]0e-kt Якщо перейти до десяткових логарифмів, тоді з рівняння стала швидкості реакції запишеться так:
де[Ао]- початкова концентрація речовини; [А]-концентрація речовини в фіксований момент часу t. Прикладами реакцій першого порядку є радіоактивний розпад, розклад деяких сполук, процеси ізомеризації. Велика кількість реакцій гідролізу, в яких бере участь розчинник, відносять до реакцій першого порядку. Прикладом можу бути процес гідролізу сахарози з утворенням глюкози і фруктози, який проходить у розбавлених розчинах за каталітичної дії кислот. До реакцій другого порядку (А+В→Р) належать реакції, швидкість яких пропорційна концентрації двох реагуючих речовин. Реакції третього порядку зустрічаються досить рідко, в цьому випадку швидкість пропорційна добутку трьох концентрацій. Відомі реакції, швидкість яких взагалі не залежить від концентрації реагуючих речовин – реакції нульового порядку. Якщо швидкість реакції не залежить від концентрації, тобто V=k, тоді це – реакція нульового порядку. Наприклад, коли концентрація ферменту підтримується постійною, а концентрація субстрату настільки перевершує її, що фермент повністю «насичений» субстратом, ферментативна реакція перебігає з постійною максимальною швидкістю, яка не залежить від подальшого збільшення концентрації субстрату. Таким чином, порядок реакції характеризує формально кінетичну залежність швидкості реакції від концентрації реагуючих речовин, а молекулярність – елементарний механізм окремих стадій більш складного процесу. Порядок і молекулярність збігаються тільки для простих за механізмом реакцій. 3. Швидкість реакції зростає з підвищенням температури. Найсуттєвішим фактором, який визначає характер впливу температури на швидкість реакції, є кінетична енергія реагентів. Добре відоме емпіричне правило Вант-Гоффа, згідно з яким при підвищенні температури на 10 градусів швидкість реакціїх зростає у 2-3 рази. Відношення сталих швидкостей реакцій при двох температурах, які відрізняються на 10 градусів, позначають Q10 і називають температурним коефіцієнтом швидкості реакції:
Правило Вант-Гоффа наближене, оскільки температурний коефіцієнт змінюється разом зі зміною температури. Більш точну залежність швидкості реакції або константи швидкості від температури дає рівняння Арреніуса:
де А – передекспоненціальний множник, який характеризує частоту зіткнень молекул, Еа – енергія активації, Т – температура, R – універсальна газова стала. Прологарифмувавши рівняння Арреніуса, отримуємо:
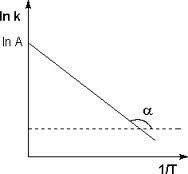
З виразу видно, що ln k (ln v) лінійно залежить від оберненої температури 1/Т. Якщо по осі ординат відкласти ln k, а по осі абсцис 1/Т, це буде графічне зображення експериментальних даних у координатах Арреніуса. З нахилу лінії легко визначається енергія активації.
Рис. 1.3. Графік Арреніуса
Найточніше залежність константи швидкості реакції від температури визначається відповідно до теорії абсолютних швидкостей у вигляді рівняння Ейрінга:
де kо-стала Больцмана (1,38∙10-23 Дж∙К-1); h-стала Планка (6,626∙10-34 Дж∙с); ∆S-зміна ентропії під час хімічного перетворення. 4. Ензиматична кінетика вивчає закономірності впливу хімічної природи реагуючих речовин (ензиму, субстратів) та умов їх взаємодії (концентрації, температури, рН середовища, присутності активаторів чи інгібіторів) на швидкість ензиматичної реакції. Кінетика ензиматичних реакцій, загалом підпорядковуючись основним засадам хімічної кінетики, все ж має ряд відмітностей, зумовлених специфікою біологічних каталізаторів. Однак проведені понад століття тому дослідження кінетики ензиматичних реакцій показали, що швидкість реакції Е+S →E+P, усупереч теоретичним очікуванням, не залежить від концентрації ензиму і субстрату так, як у випадку звичайної хімічної реакції другого порядку. Пояснення даного ефекту вперше висловлене А. Брауном (1902) та В. Анрі (1903), які пов’язували спостережувану невідповідність утворенням ензим-субстратного комплексу в ході біологічного каталізу та ефектом насичення ензиму при високій концентрації субстрату. У вигляді математичної моделі вперше уявлення про існування активного комплексу ензим-субстрат представлено в 1913 р. Л. Міхаелісом і М. Ментен. Згідно з цією моделлю ензиматичний процес можна описати як зворотну взаємодію ензиму з субстратом, у результаті якої утворюється комплекс, який надалі розпадається з утворенням продуктів реакції та регенерацією вихідного ензиму:
де Е – ензим, S – субстрат, ES – ензим-субстратний комплекс, P – продукт, k+1 – константа швидкості реакції утворення ензим-субстратного комплексу (2-го порядку), k-1 – константа швидкості розпаду ензим-субстратного комплексу (1-го порядку), k+2 – константа швидкості реакції розпаду ензим-субстратного комплексу з утворенням продуктів реакції (1-го порядку). Визначимо швидкість утворення ензим-субстратного комплексу:
Швидкість розпаду комплексу ES зумовлюється двома процесами – дисоціацією комплексу на вихідні компоненти та розпадом з утворенням продукту реакції.
Модель Міхаеліса-Ментен передбачає ряд спрощень: · у реакції бере участь лише один субстрат; · у реакції утворюється лише одна проміжна сполука – кінетично стійкий ензим-субстратний комплекс; · друга стадія реакції незворотна (беремо до уваги лише початкові швидкості); · концентрація субстрату не змінюється в ході реакції ([S]=[S]0); · концентрація ензиму мала у порівнянні з концентрацією субстрату ([E]0<<[S]0 – надлишок субстрату); · рівновага елементарної стадії Е+S↔ES установлюється дуже швидко у порівнянні зі швидкістю наступної стадії, розпад комплексу на вихідні компоненти більш імовірний, ніж розпад з утворенням продукту, тобто k+2<< k+1, k-1. У цьому випадку друга стадія реакції практично не впливає на першу і константа КS є константою дисоціації ензим-субстратного комплексу. Згідно з останнім припущенням:
Наведене рівняння містить концентрації ензиму і субстрату, що відрізняються від початкових. Стосовно субстрату, то вище було оговорено спрощення щодо незмінності його концентрації в ході реакції, тобто різницею в початковій та існуючій концентраціях субстрату можна знехтувати. На противагу цьому, існуюча концентрація ензиму суттєво відрізняється від його загальної (початкової) концентрації [E]0 внаслідок зв’язування частини молекул ензиму в склад ензим-субстратного комплексу.
Отже, з рівняння матеріального балансу [E]0=[E]+[ES] одержуємо: [E]=[E]0 – [ES] Указане значення концентрації ензиму підставляємо в попереднє рівняння:
Оскільки швидкість розпаду ензим-субстратного комплексу з утворенням продукту реакції дорівнює k+2[ES], то, підставляючи одержане значення [ES] одержимо:
Реакція досягає максимальної швидкості, коли весь ензим знаходиться в комплексі з субстратом, отже Vmax= k+2[ES]max= k+2[E]0. За умови надлишкової концентрації субстрату ([E]0<<[S]0), що прийнято як одне з припущень рівноважної кінетики ензиматичної реакції, одержимо:
Зауважимо, що класичне рівняння Міхаеліса–Ментен справедливе лише при дотриманні цілого ряду передумов і носить дещо обмежений характер. 5. У 1925 році Г.Е. Бріггсом і Дж.Б.С. Холдейном зроблена спроба вдосконалення моделі рівноважної кінетики Міхаеліса та Ментен, зокрема зняттям припущення щодо k+2<< k-1. Їх принцип стаціонарності примінимий для випадку, коли k+1 ≈ k-1 ≈ k+2 , а [E]0<<[S]0. Для кінетичних кривих, що описують ензиматичні реакції за подібних умов, можна виділити два характерних часових інтервали – стаціонарний та передстаціонарний (індукційний). Індукційний період передує стаціонарному, в ньому умова постійності концентрації [ES] не виконується. У стаціонарному інтервалі концентрація ензим-субстратного комплексу є незмінною ([ES]=const, d[ES]/dt=0). Це значить, що для початкової швидкості реакції, тобто в момент, коли зворотна реакція ще не відбувається, а індукційний період уже пройшов, кількість утвореного ензим-субстратного комплексу внаслідок надлишку субстрату дорівнює кількості такого, що розпався, тобто:
Дріб Загалом, за величиною константи Міхаеліса можна судити про специфічність зв’язування ензиму з субстратом та міцність ензим-субстратного комплексу, оскільки КМ характеризує схильність комплексу до дисоціації на ензим і субстрат: менше значення КМ відповідає більш міцному зв’язуванню субстрату з ензимом. Порівнюючи значення КМ для різних субстратів можна виявити, які з них найбільш специфічні для зв’язування. Як уже було зазначено, відношення k-1/k+1 є константою дисоціації ензим-субстратного комплексу KS , тому:
Очевидно, що константа Міхаеліса завжди більша від субстратної константи на величину k+2/k+1 Якщо k+2<< k-1, тобто виконується умова рівноважності системи, то величиною k+2 можна знехтувати і константа Міхаеліса виявляється такою, що дорівнює константі дисоціації субстрату:
Отже, теорія рівноважності Міхаеліса–Ментен може розглядатися як один з випадків більш загальної теорії стаціонарного стану. У деяких випадках k-1<< k+2, тоді константа Міхаеліса називається кінетичною константою Кк і дорівнює:
Як уже було показано вище, З рівняння матеріального балансу знаходимо [E]=[E]0 – [ES]. Тоді:
За допомогою вже застосовуваних вище у випадку з КS математичних перетворень приходимо до виразу
Оскільки швидкість утворення продукту реакції дорівнює k+2[ES], то
Це рівняння ідентичне рівнянню Міхаеліса за винятком того, що замість КS використовується КМ. Залежність швидкості ензиматичної реакції від концентрації субстрату є гіперболічною функцією (рис. 5.1.)
Рис 5.1. Залежність швидкості ензиматичної реакції від концентрації субстрату При невеликих концентраціях субстрату швидкість реакції пропорційна його вмісту, надалі при збільшенні [S] спостерігається відхилення від лінійної залежності і, насамкінець, при високих концентраціях субстрату подальше збільшення [S] не впливатиме на швидкість ензиматичної реакції. Розглянемо детальніше математичне пояснення даних змін. При порівняно малих концентраціях субстрату, коли [S]<<KM, можна прийняти, що KM+[S]≈ KM, тоді:
тобто швидкість реакції є лінійною функцією концентрації субстрату. У випадках, коли [S]>>KM (велика концентрація субстрату або ензим добре зв’язує субстрат, чому відповідає низька KM), то величиною константи Міхаеліса можна знехтувати і швидкість реакції буде дорівнювати:
Ензим виявляється насиченим субстратом, вільного ензиму в реакційній суміші немає, тому подальше збільшення [S] не впливатиме на хід реакції, а швидкість набуває максимального значення.
У випадку, коли швидкість дорівнює половині максимальної (V=Vmax/2), після певних математичних перетворень константа Міхаеліса дорівнюватиме концентрації субстрату. Підставляємо значення V у рівняння Бріггса–Холдейна:
Розділимо обидві частини рівняння на Vmax.
Отже, KM має розмірність концентрації. Константа Міхаеліса дорівнює тій концентрації субстрату, при якій швидкість ензиматичної реакції дорівнює половині максимальної. Отже, відрізок на осі абсцис, що відповідає Vmax/2 і буде KM. Для практичного визначення кінетичних параметрів ензиматичної реакції користуватись графіком Міхаеліса–Ментен, побудованим в прямих координатах, незручно. Рівняння Міхаеліса описує гіперболу і визначення Vmax і KM згідно з цією залежністю потребує даних у всьому діапазоні концентрацій. Зокрема, існує необхідність використання високих концентрацій субстрату, які «насичують» ензим, що не завжди може бути досягнуто через обмежену розчинність субстрату. Крім того, Vmax згідно з таким графіком визначається недостатньо точно. Тому існує ряд підходів до перетворення рівняння Міхаеліса–Ментен для досягнення лінійної залежності та зображення на графіку у вигляді прямої лінії. Найбільш відомим і популярним є метод Лайнуівера–Берка, суть якого зводиться до перетворення рівняння Бріггса-Холдейна за методом подвійних зворотних величин. Якщо
Останній вираз і носить назву рівняння Лайнуівера–Берка. Графік цього рівняння – пряма лінія, побудована у координатах 1/V та 1/S (рис. 5.2).
Рис. 5.2. Графік Лайнуівера–Берка Для визначення максимальної швидкості та константи Міхаеліса пряму продовжують до її перетину з віссю абсцис і ординат. Відповідно, значення Vmax дорівнює зворотній величині відрізка, що відсікається прямою на осі ординат; значення KM дорівнює зворотній величині відрізка, що відсікається прямою на осі абсцис. Крім того, тангенс кута нахилу прямої дорівнює величині KM/ Vmax, отже ці величини, окрім визначення через довжини відрізків, можна розрахувати з даних нахилу прямої. Однак, незважаючи на істотні переваги графіка Лайнуівера–Берка, він не позбавлений недоліків. Зокрема, положення прямої визначається точками в ділянці низьких концентрацій субстрату, де визначення менш надійне, тоді як точки в ділянці високих концентрацій розташовуються досить густо. Інгібування прийнято поділяти на кілька варіантів – конкурентне, неконкурентне та безконкурентне. Але такий поділ не досконалий, оскільки, наприклад, неконкуренте інгібування може бути як оборотним, так і необоротним.
Поиск по сайту: |

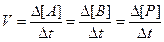
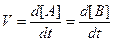
 ,
,




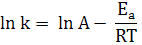




 – швидкість зворотної реакції
– швидкість зворотної реакції – швидкість розпаду з утворенням продукту.
– швидкість розпаду з утворенням продукту. , отже
, отже 
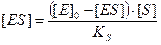



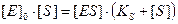


 – рівняння Міхаеліса–Ментен
– рівняння Міхаеліса–Ментен
 називають константою Міхаеліса КМ. Вона характеризує співвідношення швидкостей розпаду (чисельник) і утворення (знаменник) ензим-субстратного комплексу.
називають константою Міхаеліса КМ. Вона характеризує співвідношення швидкостей розпаду (чисельник) і утворення (знаменник) ензим-субстратного комплексу.

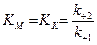
 .
.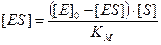

 ,або
,або – рівняння Бріггса–Холдейна
– рівняння Бріггса–Холдейна