 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Равнопеременное криволинейное движение
Если во все время движения величина касательного ускорения точки постоянна, т.е. aτ = const, то криволинейное движение называется равнопеременным. При этом следует помнить, что если направление aτ совпадает с направлением скорости, то движение называется равноускоренным, если же aτ направлено в сторону, противоположную скорости, то - равнозамедленным (рис. 2.15). Рассмотрим более подробно это движение. Найдем закон изменения скорости точки и ее закон движения по криволинейной траектории s = s(t), считая, что при t=0 s = s0, а v= v0. Здесь s0 - начальное расстояние от начала отсчета; v0 - начальная скорость точки. Тогда из выражения
интегрируя, найдем закон изменения скорости точки
интегрируя, получим закон равнопеременного криволинейного движения:
Отметим, что формулы (2) и (3) отличаются от соответствующих формул для случая прямолинейного движения точки тем, что в эти формулы входит касательное ускорение. Рассмотрим теперь, как определяется ускорение точки при ее движении по окружности радиусом R (рис. 2.16).
Скорость точки в случае ее движения в положительном направлении отсчета расстояний определим по полученной выше формуле:
Дифференцируя это равенство по времени, получим касательное ускорение:
Величина:
Нормальное ускорение получим, принимая во внимание, что радиус кривизны окружности равен ее радиусу, т. е. ρ = R:
Модуль ускорения точки в круговом движении
Угол μ, который образует ускорение с радиусом окружности, определяется из равенства
Если V=const, то ускорение в круговом движении будет направлено по радиусу, так как тангенциальное ускорение в этом случае равно нулю.
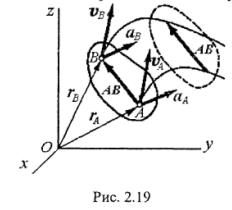
11. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА Поступательным движением твердого тела называется такое движение, при котором любая прямая, проведенная в теле во все время движения, остается параллельной своему первоначальному направлению. При поступательном движении точки тела могут двигаться по любым траекториям. Рассмотрим движение тела относительно некоторой системы координат (рис. 2.19). Возьмем в теле точку А. Векторное уравнение движения точки А имеет вид: rA = rA(t). Возьмем в теле другую точку В, определяемую радиус-вектором rB. Векторное уравнение движения точки В имеет вид:
При движении тела радиус-векторы rA и rB изменяются с течением времени и по модулю, и по направлению. Вектор АВ имеет постоянный модуль и постоянное направление, что следует из определения абсолютно твердого тела и его поступательного движения. Как видно из уравнения (2), траекторию точки В можно получить параллельным переносом траектории точки А. Направление и величина этого переноса определяются вектором АВ. Таким образом, при поступательном движении твердого тела все его точки описывают одинаковые траектории, которые при параллельном переносе совпадают. Дифференцируя равенство (2) по времени, найдем:
Далее, учитывая, что VB=VA При вторичном дифференцировании: aB=aA Так как точки А и В были выбраны произвольно, то формулы (4) и (5) показывают, что при поступательном движении все точки твердого тела движутся с одинаковыми скоростями и ускорениями для любого момента времени. Из этих свойств поступательного движения следует, что изучение поступательного движения тела сводится к изучению движения какой-либо одной из его точек. Следовательно, при изучении поступательного движения твердого тела можно применять все формулы, рассмотренные выше при исследовании движения одной точки.
12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ВОКРУГ НЕПОДВИЖНОЙ ОСИ Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения.
φ =2π N (1) При вращении тела угол поворота изменяется с течением времени, т.е. φ = φ (t) (2) Равенство (2) называется уравнением, или законом вращательного движения твердого тела вокруг неподвижной оси. Рассмотрим теперь основные кинематические величины, характеризующие вращательное движение тела. Этими величинами являются угловая скорость тела ω и угловое ускорение ε. Угловой скоростью тела называется физическая величина, характеризующая быстроту изменения угла поворота φ тела во времени, т.е.:
В самом деле, пусть за промежуток времени ∆t угол поворота φ получил приращение ∆φ. Тогда средняя угловая скорость определится равенством:
Предел этого отношения при ∆t→0 называют угловой скоростью тела в данный момент времени
Мы вновь пришли к равенству (3). Итак, угловая скорость тела равна первой производной по времени от угла поворота тела. Значение угловой скорости ω для данного момента времени может быть положительным или отрицательным в зависимости от того, возрастает или убывает угол поворота тела. Если ω > 0, то тело в данный момент времени вращается в положительном направлении отсчета угла поворота φ, т. е. против движения часовой стрелки. Размерность угловой скорости [ω]=с-1. В технике угловую скорость характеризуют числом оборотов в минуту и обозначают буквой n. Замечая, что n об/мин соответствует n/60 об/с и что 1 оборот соответствует 2π радианам, получим:
Эту меру быстроты изменения угловой скорости можно получить как предел приращения угловой скорости к приращению времени:
Эту меру быстроты изменения угловой скорости можно получить как предел приращения угловой скорости к приращению времени:
Таким образом, угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скорости или второй производной от угла поворота. Размерность углового ускорения [ε] = с-2. Если знаки угловой скорости и углового ускорения одинаковы, то вращение тела в данный момент ускоренное, если же знаки ω и ε различны, вращение замедленное. 13. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ Вращение тела называют равномерным, если угловая скорость тела постоянна, т.е. ω =const. В этом случае:
Произвольную постоянную С определяем из начального условия φ = φ0 + ωt (2) Равенство (2) называется законом равномерного вращательного движения твердого тела. При φ0=0 это равенство упрощается. Равнопеременным вращением называется такое вращательное движение тела, при котором его угловое ускорение постоянно, т.е. ε = const ≠ 0. В этом случае:
Из начального условия Равенство (4) называется законом изменения угловой скорости при равнопеременном вращательном движении тела. Далее
Из начального условия Тогда окончательно
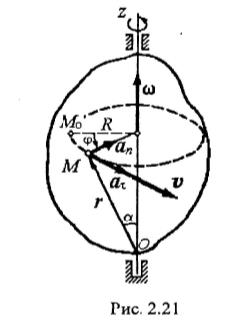
Равенство (6) называется законом равнопеременного вращательного движения твердого тела. Легко заметить аналогию между полученными формулами (2) и (6) и формулами равномерного и равнопеременного движения точки. Соответствующие формулы совпадают с точностью до обозначений.
14. СКОРОСТЬ ТОЧЕК, ВРАЩАЮЩИХСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Пусть вращение тела вокруг неподвижной оси задано уравнением
Найдем распределение скоростей точек тела при его вращении. Воспользуемся при этом естест венным способом задания движения точки. Рассмотрим движение какой-нибудь точки М тела. При вращении тела точка М будет описывать окружность, радиус которой обозначим R (рис. 2.21). Составим уравнение движения точки М по ее траектории. За начало отсчета примем начальное положение М0, а за положительное направление дуги s - направление отсчета угла поворота φ. Тогда уравнением движения точки М по ее траектории будет S = M0M = Rφ (2) а следовательно, проекция скорости точки М на направление касательной определится следующим образом:
Эту скорость точки М, в отличие от угловой скорости тела, часто называют линейной скоростью. Таким образом, линейная скорость какой-либо точки вращающегося твердого тела равна произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор v скорости точки М направлен по касательной к окружности, которую описывает точка М, т.е. перпендикулярен к радиусу этой окружности. Модуль v вектора скорости v равен . Так как угловая скорость ω является кинематической характеристикой всего тела в целом, то из формулы (5) следует, что скорости точек тела пропорциональны расстояниям этих точек до оси вращения.
15. УСКОРЕНИЕ ТОЧЕК, ВРАЩАЮЩИХСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Ускорение точки М находим, определив сначала касательное и нормальное ускорения:
Тогда модуль полного ускорения точки М:
Угол, образованный вектором ускорения точки М с радиусом описываемой точкой окружности, определяется так:
Из формулы (8) следует, что ускорения точек вращающегося тела образуют в данный момент один и тот же угол α с радиусами описываемых ими окружностей. В частном случае равномерного вращения ε=0, поэтому α=0 и, следовательно, полное ускорение по модулю равно нормальному и направлено к оси вращения.
16. векторная формула для скорости точек тела, вращающихся вокруг неподвижной оси
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси Oz с угловой скоростью r = x(t)i + y(t)j + z(t)k(1) Здесь следует заметить, что в разложении (1) х, у, z и вектор к постоянны, т.е. не зависят от времени, а i и j зависят от времени, так как вращаются вместе с телом. Тогда для скорости точки М имеем
Производные от единичных векторов, входящие в формулу (2), есть скорости концов этих векторов. Например, при φ > 0 вектор скорости конца i направлен параллельно j в положительном направлении оси Оу, а вектор скорости конца j направлен параллельно iв отрицательном направлении оси Ох. Модуль каждой из этих скоростей равен Тогда Далее, учитывая, что
Подставляя формулы (3) в равенство (2) и используя то, что
Назовем вектор
Как видно из равенства (5), вектор угловой скорости тела направлен вдоль оси вращения так, чтобы наблюдатель, смотрящий с его конца, видел вращение тела против хода часовой стрелки. Вектор со можно расположить в любом месте оси вращения, т.е. СО - скользящий максиальный вектор. Перепишем теперь формулу (4) с учетом (5), тогда
Вектор скорости любой точки тела, вращающегося вокруг неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведенный из произвольного центра, взятого на оси вращения. Формула (6) называется формулой Эйлера.
Примечание. Так как вектор r изменяется со временем только по направлению, то
где ω - угловая скорость поворота вектора r. Формула (а) определяет правило дифференцирования вектора, постоянного по модулю. Аналогично из равенств (3) и (5) получаем:
Модуль скорости точки М:
что совпадает с формулой (5) по времени, получим вектор углового ускорения:
Вектор углового ускорения ε, так же как и вектор угловой скорости ω, лежит на оси вращения. При этом в случае ускоренного вращения вектор ε направлен в ту же сторону, что и вектор ω, в случае же замедленного вращения вектор ε направлен в сторону, противоположную вектору ω. Для определения проекций скорости точки М на оси выбранной подвижной системы координат представим формулу (6) в виде определителя третьего порядка:
Отсюда:
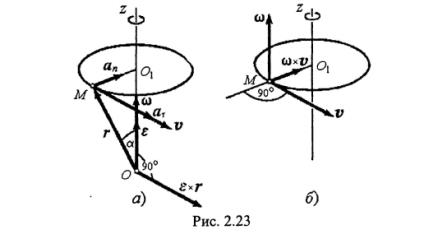
Равенства (10) определяют проекции скорости любой точки М вращающегося тела на выбранные оси координат. Выведем теперь векторную формулу для определения ускорения произвольной точки М тела, вращающегося вокруг неподвижной оси. Для этого продифференцируем равенство (6) по времени. В результате получим
Из рис. 2.23 видно, что вектор
Из формул (13) находим:
Т.е. приходим к известным ранее равенствам. Далее, если взять систему осей координат Oxyz, в которой ось z направлена вдоль оси вращения, и представить anв виде an=-ω2∙O1M, то, согласно (12) и (13)
Отсюда получаем:
Равенства (15) дают проекции ускорения любой точки М(х, у, z) вращающегося тела на выбранные оси координат.
Пусть плоская фигура движется относительно неподвижной системы координат Оху. В этой системе положения полюса А и произвольной точки В определяются соответственно радиус-векторами Вектор Дифференцируя обе части равенства (1) по времени, получим: В полученном равенстве (2) Вектор Следовательно, скорость Таким образом, определив вращательную скорость
Поиск по сайту: |
 , или
, или  ,
, . Далее, принимая во внимание, что
. Далее, принимая во внимание, что 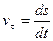 , и вторично
, и вторично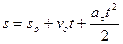 .
.
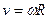 (4)
(4)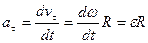 .
.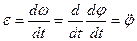 называется угловым ускорением вращения радиуса OM=R.
называется угловым ускорением вращения радиуса OM=R.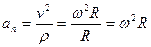

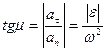
 rB= rA+AB
rB= rA+AB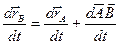
 , а вектор АВне изменяется во времени ни по величине, ни по направлению, и следовательно, производная
, а вектор АВне изменяется во времени ни по величине, ни по направлению, и следовательно, производная  , имеем
, имеем Рассмотрим вопрос о задании уравнения, или закона вращательного движения. Пусть ось Oz является неподвижной осью, вокруг которой вращается тело. Проведем через ось Oz две плоскости: подвижную Р и неподвижную Q (рис. 2.20). Положение вращающегося тела может быть опре делено двугранным углом φ между этими плоскостями. Назовем угол φ углом поворота тела и условимся считать положительным, если, глядя с положительного конца оси z, угол φ виден отложенным от неподвижной плоскости против хода часовой стрелки. Угол поворота тела обычно измеряют в радианах. Иногда в практических задачах этот угол выражают числом оборотов N тела. Так как один оборот тела соответствует 2π радиан, то получаем зависимость
Рассмотрим вопрос о задании уравнения, или закона вращательного движения. Пусть ось Oz является неподвижной осью, вокруг которой вращается тело. Проведем через ось Oz две плоскости: подвижную Р и неподвижную Q (рис. 2.20). Положение вращающегося тела может быть опре делено двугранным углом φ между этими плоскостями. Назовем угол φ углом поворота тела и условимся считать положительным, если, глядя с положительного конца оси z, угол φ виден отложенным от неподвижной плоскости против хода часовой стрелки. Угол поворота тела обычно измеряют в радианах. Иногда в практических задачах этот угол выражают числом оборотов N тела. Так как один оборот тела соответствует 2π радиан, то получаем зависимость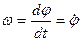 (3)
(3) (4)
(4) (5)
(5)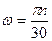 c-1 (6)
c-1 (6)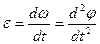 (7)
(7)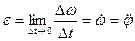 (8)
(8)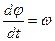

 (1)
(1) . В результате находим С = φ0. Тогда:
. В результате находим С = φ0. Тогда: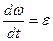 ,
, 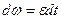 ,
,  (3)
(3) находим С1 = ω0. Тогда ω = ω0 + εt (4)
находим С1 = ω0. Тогда ω = ω0 + εt (4)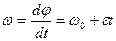 ,
,  ,
, 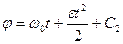 (5)
(5)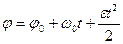 (6)
(6)
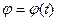 (1)
(1) (3) или
(3) или (4)
(4)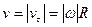 (5)
(5)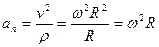 (6)
(6)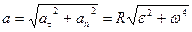 (7)
(7) (8)
(8) . Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с телом (рис. 2.22). В этом случае
. Определим скорость произвольной точки М этого тела. Введем прямоугольную систему координат с началом на оси вращения и неизменно связанную с телом (рис. 2.22). В этом случае (2)
(2)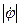 .
. ,
, 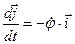
 , а
, а 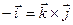 , получим
, получим , а
, а  (3)
(3) , найдем:
, найдем: (4)
(4) вектором угловой скорости ω, тогда
вектором угловой скорости ω, тогда 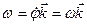 . (5)
. (5)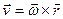 (6)
(6) , то из (6) следует, что если
, то из (6) следует, что если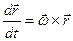 , (а)
, (а)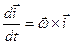
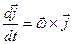
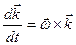 (б)
(б)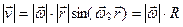 (7),
(7),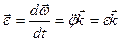 (8)
(8) . (9)
. (9)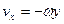 ,
,  ,
,  . (10)
. (10) (11) , или
(11) , или  (12)
(12) направлен по касательной к траектории, а вектор
направлен по касательной к траектории, а вектор  - по радиусу МО1, т.е. по главной нормали к траектории. Следовательно,
- по радиусу МО1, т.е. по главной нормали к траектории. Следовательно, ,
,  (13)
(13)

 (14)
(14) ,
,  ,
,  . (15)
. (15)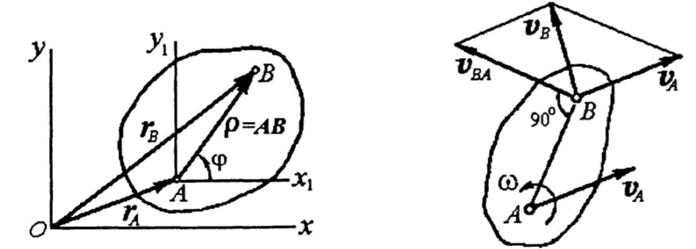
 и
и 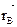 . Между этими векторами
. Между этими векторами  в любой момент времени имеет место следующее соотношение:
в любой момент времени имеет место следующее соотношение: 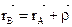 (1).
(1). , перемещающейся вместе с полюсом А поступательно. Подчеркнем еще раз, что движение сечения по отношению к осям
, перемещающейся вместе с полюсом А поступательно. Подчеркнем еще раз, что движение сечения по отношению к осям 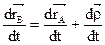 (2).
(2). ,
, 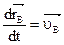 . Что же касается
. Что же касается 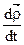 , то это - скорость, которую точка В получает при вращении вокруг полюса А. Обозначим эту скорость через
, то это - скорость, которую точка В получает при вращении вокруг полюса А. Обозначим эту скорость через  .
. . Тогда формула распределения скоростей примет вид:
. Тогда формула распределения скоростей примет вид: 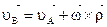 или
или  .
. любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости
любой точки плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости  другой, произвольно выбранной и принятой за плюс, точки А и скорости
другой, произвольно выбранной и принятой за плюс, точки А и скорости 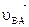 точки В в ее вращении вместе с плоской фигурой вокруг этого полюса. Вектор
точки В в ее вращении вместе с плоской фигурой вокруг этого полюса. Вектор  .
.