 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вимушені коливання. Резонанс
Лекція 12 . Вимушені коливання. Резонанс. План. 1. Згасаючі коливання. 2. Вимушені коливання. Резонанс. 3. Осцилятор як приклад Фур’є-розкладу. Згасаючі коливання.
Коливальна система, виведена з положення рівноваги, врешті-решт припинить коливальний рух через втрату механічної енергії на подолання сил опору середовища та створення коливань у навколишньому середовищі. При цьому амплітуда коливань поступово зменшується до нуля. Такі коливання, які відбуваються з поступовою втратою запасу енергії коливальної системи, називаються згасаючими. Розглянемо коливання, швидкість яких невелика, а тому сила опору середовища пропорційна швидкості.
b- коефіцієнт опору середовища. Якщо на систему діють пружні або квазіупружні сили, то другий закон Ньютона прийме вигляд:
Поділимо на масу та отримаємо диференційне рівняння:
За умови, що β<ω0 розв’язок такого рівняння має вигляд:
A(t) – амплітуда затухаючих коливань; ω – циклічна частота коливань. Визначимо закон зміни амплітуди та частоту затухаючих коливань за умови, що енергія системи витрачається на подолання сил опору середовища.
Зменшення енергії тим повільніше, чим менша сама енергія. Розділимо змінні в отриманому рівнянні та розв’яжемо його:
Значення сталої С визначимо з початкових умов: при t=0 E=E0 , отже C=lnE0 . Тоді розв’язок набуває вигляду:
Оскільки механічна енергія пропорційна квадрату амплітуди, можна зробити висновок, що Тобто амплітуда згасаючих коливань зменшується по експоненті:
У загальному випадку закон зменшення амплітуди коливань залежить від характеру сил опору. Враховуючи рівняння (2), рівняння руху (1) приймає вигляд: Частоту згасаючих коливань ω визначаємо, підставляючи вирази для х, Період згасаючих коливань: · При незначних силах опору ( β > 0 ) період коливання системи збільшується, а частота – зменшується. · При значних силах опору ( β = ω ) система, виведена зі стану рівноваги, не здійснює коливань, а поступово наближається до стану рівноваги. Такий рух називають аперіодичним. Відношення амплітуди на початку і в кінці періоду є величина стала для всього процесу коливань і називається декрементом згасання. Натуральний логарифм від цього виразу називається логарифмічним декрементом згасання:
Часом релаксації τ називається проміжок часу, за який амплітуда коливання зменшується в е разів:
Звідки βτ=1 Отже Добротністю коливальної системи Q називається відношення енергії коливальної системи в даний момент часу до втрати енергії за один період, помножене на 2π:
Розкладання функції
Чим більше добротність коливальної системи, тим менше згасання коливань. Коливання вважають такими, що припинилися, якщо їх амплітуда зменшується в 10 разів. В цьому випадку число помітних коливань системи зв’язане з добротністю співвідношенням:
Вимушені коливання. Резонанс. Для підтримки незгасаючих коливань системи необхідно періодично поповнювати енергію, яка витрачається на подолання сил опору середовища. Поповнення можна здійснювати періодично діючи зовнішньою силою, яка змінюється за часом за гармонічним законом: В виразі F0 = амплітуда зовнішньої сили, ω – її циклічна частота. Такі коливання називають вимушеними, а силу – змушуючою силою. Диференційне рівняння вимушених коливань під дією пружної або квазіпружної сили за умови, що сила опору пропорційна швидкості коливань, приймає вигляд:
Поділимо на масу та введемо позначення:
Отримане рівняння є неоднорідним диференційним рівнянням другого порядку. Його розв’язок є сумою розв’язку відповідного однорідного рівняння і частинного розв’язку неоднорідного рівняння. Знайдемо частинний розв’язок, вважаючи, що встановилися гармонічні коливання з частотою змушуючої сили ω. Розв’язок шукатимемо у вигляді:
А – амплітуда коливань, що встановилися; φ – зсув фаз між зміщенням та змушуючою силою. Підставляючи вирази для х,
Рівняння вимушених коливань зміщення має вигляд:
Амплітуда таких коливань є функцією частоти ω , яка набуває максимального значення при певних умовах. Явище різкого зростання амплітуди коливань при частотах ω змушуючої сили близьких до резонансної частоти ωрез називають резонансом. Амплітуда максимальна при мінімальному значенні підкореневого виразу, тобто похідна від нього за частотою дорівнює нулю. Дослідження на екстремум підкореневого виразу дає змогу визначити резонансну частоту
Незгасаючі коливання можуть збуджуватися не тільки внаслідок дії періодичної сили, але й при періодичній зміні параметрів коливальної системи. Такі коливання називають параметричними. При певній частоті зміни параметрів амплітуда коливань зростає. Таке явище називається параметричним резонансом.
Поиск по сайту: |



 - власна частота вільних коливань системи;
- власна частота вільних коливань системи; - коефіцієнт згасання коливань.
- коефіцієнт згасання коливань. (1)
(1)




 , (2)
, (2)


 та
та  в диференційне рівняння
в диференційне рівняння 




 .
.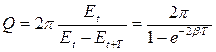
 в ряд Тейлора при βТ<<1дає вираз:
в ряд Тейлора при βТ<<1дає вираз:
 , звідки
, звідки 
 .
.
 ,
,  ,
, 
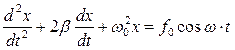 (1)
(1)
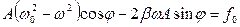

 звідки
звідки 
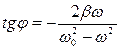


 Резонансне значення амплітуди визначається формулою:
Резонансне значення амплітуди визначається формулою:
 · Резонансна частота при згасанні коливань завжди менше власної частоти системи.
При незначному згасанні та наближенні резонансної частоти до власної частоти системи резонансна амплітуда нескінченно зростає, що приводить до руйнування системи.
· Резонансна частота при згасанні коливань завжди менше власної частоти системи.
При незначному згасанні та наближенні резонансної частоти до власної частоти системи резонансна амплітуда нескінченно зростає, що приводить до руйнування системи.