|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАДАЧ
Элементы векторной алгебры, аналитической геометрии И линейной алгебры
Задача 1 Даны координаты вершин пирамиды А1А2А3А4. Требуется найти: 1) Угол между ребрами А1А2 и А1А4; 2) Площадь грани А1А2А3; 3) Уравнение плоскости А1А2А3; 4) Объем пирамиды; 5) Уравнения и длину высоты, опущенной из вершины А4 на грань А1А2А3; 6) Проекцию А1А4 на плоскость А1А2А 3; 7) Уравнение плоскости, параллельной А1 А2 А4, проходящей через А3 8) Угол между плоскостями А1А2А3, А1А2А4: 9) Выполнить чертеж пирамиды в пространстве.
1.1 А1(14; 4; 5), А2(-5; -3; 2), А3(-2; -6; -3), А4(-2; 2; 1). 1.2 А1(2; -1; 2), А2( 1; 2; -1), А3( 3; 2; 1), А4(-4; 2; 5). 1.3 А1 (1; 1; 2 ), А2(-1; 1; 3), А3 (2; -2; 4 ), А4(-1; 0; -2). 1.4 А1( 2; 3; 1 ), А2( 4; 1; -2), А3( 6; 3; 7), А4( 7; 5; -3). 1.5 А1(1; 1;-1 ), А2( 2; 3; 1), А3( 3; 2; 1), А4( 5; 9; -8). 1.6 А1(1; 5; -7), А2( -3; 6; 3), А3( -2; 7; 3), А4(-4; 8; -12). 1.7 А1 (-3; 4; -7 ), А2(1; 5; -4), А3 (-5; -2; 0 ), А4(2; 5; 4). 1.8 А1( -1; 2; -3 ), А2( 4; -1; 0), А3( 2; 1; -2), А4( 3; 4; 5). 1.9 А1 (4; -1; 3 ), А2(-2; 1; 0 ), А3 (0; -5; 1 ), А4(3; 2; -6). 1.10 А1( 1; -1; 1 ), А2( -2; 0; 3), А3( 2; 1; -1), А4( 2; -2; -4). 1.11 А1(1; -4; 5), А2(5; -3; 2), А3(2; -6; -3), А4(2; 2; 1). 1.12 А1(12; -1; 2), А2( 1; -2; -1), А3( 3; -2; 1), А4(4; 2; 5). 1.13 А1 (10; 1; 2 ), А2(-1; -1; 3), А3 (2; 2; 4 ), А4(-1; 0; -2). 1.14 А1( -2; 3; 1 ), А2( 4; -1; -2), А3( 6; -3; 7), А4( 6; 5; -3). 1.15 А1(11; 1;-1 ), А2( 2; -3; 1), А3( 3; -2; 1), А4( 5; 0; -8). 1.16 А1(1; -5; -7), А2( 3; 6; 3), А3( -2; -7; 3), А4(-4; 8; -12). 1.17 А1 (3; 4; -7 ), А2(1; -5; -4), А3 (-5; 2; 0 ), А4(2; 5; -4). 1.18 А1( 1; 2; -3 ), А2( 4; 1; 0), А3( 2; -1; -2), А4( 3; -4; 5). 1.19 А1 (4; 1; 3 ), А2(-2; -1; 0 ), А3 (0; 5; 1 ), А4(3; -2; -6). 1.20 А1( 12; -1; 1 ), А2( 2; 0; 3), А3( 2; -1; -1), А4( 2; -2; -4).
Задача 2 Доказать совместность данной системы линейных уравнений и решить ее тремя способами: 1) методом Гаусса, 2) методом Крамера, 3) средствами матричного исчисления.
2.1
2.3
2.5
2.7
2.9
2.11
2.13 2.15
2.17
2.19
Введение в математический анализ
Задача 3 Найти пределы функции.
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.10
3.11 a)
б)
3.12 a)
б)
3.13 a)
б)
3.14 a)
б)
3.15 a)
б)
3.16 a)
б)
3.17 a)
б)
3.18 a)
б)
3.19 a)
б)
3.20 a)
б)
Производная и ее приложения
Задача 4 Найти производные заданных функций (в случаях г и д найти производные второго порядка
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
4.11 а) г)
4.12 а) г)
4.13 а) г)
4.14 а) г)
4.15 а) г)
4.16 а) г)
4.17 а) г)
4.18 а)
г)
4.19 а) г)
4.20 а) г) Функции нескольких переменных
Задача 5 5.1 Дана функция
5.2 Дана функция
5.3 Дана функция
5.4 Дана функция
5.5 Дана функция
5.6 Дана функция
5.7 Дана функция 5.8 Дана функция
5.9 Дана функция.
5.10 Дана функция
5.11 Дана функция
5.12 Дана функция
5.13 Дана функция
5.14 Дана функция
5.15 Дана функция
5.16 Дана функция
5.17 Дана функция
5.18 Дана функция
5.19 Дана функция
5.20 Дана функция Задача 6 Дана функция
6.1 z = 3x2y2 + 5xy2; A(1; 1),
6.2 z = 3x4 + 2x2y3; A(-1; 2),
6.3 z =ℓn(3x2 + 4y2); A(1; 3),
6.4 z = arсsin
6.5 z = arсtg ( xy2); A(2; 3),
6.6 z = 5x2 + 6xy; A(2; 1),
6.7 z =ℓn(5x2 + 4y2); A(1; 1),
6.8 z =ℓn(5x2 + 3y2); A(1; 1),
6.9 z = 2x2 + 3xy+y2; A(2; 1),
6.10 z = x2 + xy+y2; A(1; 1),
6.11
6.12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6.20
Интегралы
Задача 7 Найти неопределенные интегралы. В двух первых примерах (п. а) и б)) проверить результаты дифференцированием. 7.1 а) 7.2 а) 7.3 а) 7.4 а) 7.5 а) 7.6 а) 7.7 а) 7.8 а) 7.9 а) 7.10 а)
7.11 а)
7.12. а)
7.13. а)
7.14. а)
7.15. а)
7.16. а)
7.17. а)
7.18. а)
7.19. а)
7.20. а)
Задача 8 Вычислить площадь области, ограниченной линиями.
Дифференциальные уравнения Задача 9 Найти общие интегралы дифференциальных уравнений 9.1. а) 9.2. а) 9.3. а)
9.4. а)
9.5. а)
9.6. а) 9.7. а)
9.8. а)
9.9. а)
9.10. а)
9.11. а)
9.12. а) 9.13. а) 9.14. а)
9.15. а)
9.16. а) 9.17. а) 9.18. а) 9.19. а) 9.20. а)
Задача 10 Найти решение задачи Коши для дифференциального уравнения 10.1 10.2. 10.3. 10.4. 10.5. 10.6. 10.7. 10.8. 10.9.
10.10.
10.11.
10.12.
10.13.
10.14.
10.15.
10.16.
10.17.
10.18.
10.19.
10.20.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАДАЧ
Задача 1 Даны координаты вершин пирамиды А1А2А3А4. Требуется найти: 1) Угол между ребрами А1А2 и А1А4; 2) Площадь грани А1А2А3; 3) Уравнение плоскости А1А2А3; 4) Объем пирамиды; 5) Уравнение и длину высоты, опущенной из вершины А4 на грань А1А2А3; 6) Проекцию А1А4 на плоскость А1А2А3; 7) Уравнение плоскости, параллельной А1А2А4, проходящей через вершину А3; 8) Угол между плоскостями А1А2А3 и А1А2А4; 9) Выполнить чертеж пирамиды в пространстве. А1(2; 0; -3), А2(1; 1; -4), А3(0; -1; 3), А4(4; -2; 0).
Решение
1) Угол между ребрами А1А2 и А1А4 найдем как угол между векторами
Найдем длины векторов
Косинус угла между векторами
φ = arсcos (-0,9802)=π-arccos 0,9802= 168°36/
2) Для нахождения площади грани А1А2А3 используем векторное произведение векторов .
S∆=
S∆=
3) Найдем уравнение плоскости А1А2А3, зная, что А1(2; 0; -3), А2(1; 1; -4), А3(0; -1; 3).
5х+8y+3z-1=0 – уравнение плоскости А1А2А3.
4) Для нахождения объема пирамиды используем смешанное произведение векторов
5) Vпир.=
      H= H= 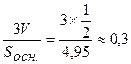 (лин.ед) – длина (лин.ед) – длина
высоты А4О
Рисунок 1 - Пирамида
Воспользуемся формулой Канонического уравнения прямой для нахождения уравнения высоты А4О, учитывая, что в качестве направляющего вектора прямой А4О служит нормаль к плоскости А1А2А3 вектор
6) Проекцией А1А4 на плоскость А1А2А3 является А1О. Из треугольника А1А4О найдем
А1А4=
А1О=
7) Сначала найдем уравнение плоскости А1А2А4 , получим:
Так как искомая плоскость параллельна А1А2А4, то нормаль у них одинаковая: Воспользуемся уравнением плоскости, проходящей через данную точку А3(0; -1; 3) .
8) Воспользуемся найденными уравнениями плоскостей А1А2А3, А1А2А4:
Угол между плоскостями равен углу между нормалями к этим плоскостям.
9) А1(2; 0; -3), А2(1; 1; -4), А3(0; -1; 3), А4(4; -2; 0)
Рисунок 2 – Чертеж пирамиды в пространстве
Задача 2 Доказать совместность данной системы линейных уравнений и решить ее тремя способами: 1) методом Крамера; 2) методом Гаусса; 3) средствами матричного исчисления
Решение
Составим матрицу системы и найдем ее ранг
Вычислим определитель этой матрицы
Следовательно,
1) Вычислим вспомогательные определители:
Находим решение системы
Ответ: (1; -2; 3)
2) Метод Гаусса – метод последовательного исключения неизвестных.
Чтобы иметь при первом неизвестном единицу в первом уравнении вычтем из второго уравнения первое, результат поставим вместо первого уравнения.
   
Для исключения коэффициентов при первом неизвестном умножим первое уравнение на 3 и вычтем из него второе уравнение, затем первое уравнение умножим на 4 и вычтем из него третье уравнение, в результате получим:
Уравняем коэффициенты при втором неизвестном, для этого второе уравнение умножим на 33, третье – на 17, затем вычтем из второго третье уравнение:
Завершили прямой ход метода Гаусса, привели систему к треугольному виду. Произведем обратный ход. Из последнего уравнения найдем
Подставим
Ответ: (1; -2; 3)
3) Введем матрицы
Найдем алгебраические дополнения
Найдем матрицу Х , учитывая, что
Ответ: (1; -2; 3)
Задача 3 Найти пределы функций, не пользуясь правилом Лопиталя
1) 2)
Решение
1) а)
б)
в)
Поиск по сайту: |
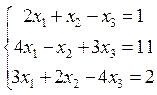 2.2
2.2 
 2.4
2.4 
 2.6
2.6 
 2.8
2.8 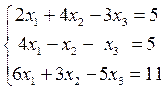
 2.10
2.10 
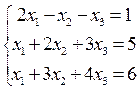 2.12
2.12 
 2.14
2.14 
 2.16
2.16 
 2.18
2.18 
 2.20
2.20 



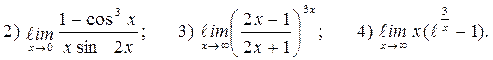









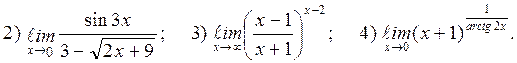






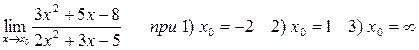

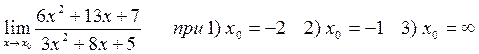


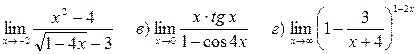

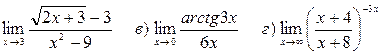










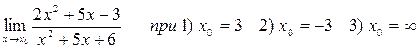


 ).
).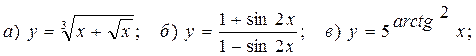
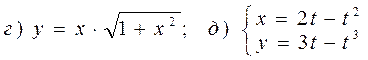
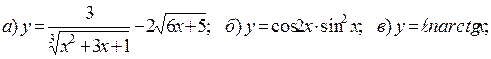




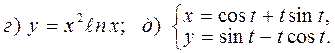

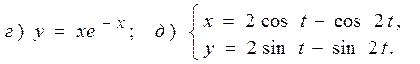



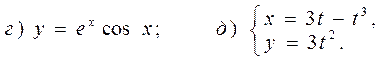
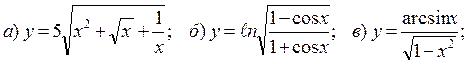
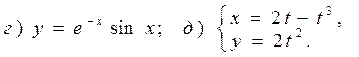




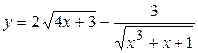 б)
б) 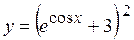 в)
в) 
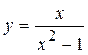 д)
д) 
 б)
б)  в)
в) 
 д)
д) 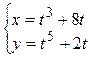
 б)
б)  в)
в) 
 д)
д) 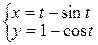
 б)
б)  в)
в) 
 д)
д) 
 б)
б)  в)
в) 
 д)
д) 
 б)
б) 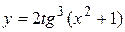 в)
в) 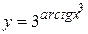
 д)
д) 
 б)
б)  в)
в) 
 д)
д) 
 б)
б)  в)
в) 
 д)
д) 
 б)
б)  в)
в) 
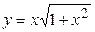 д)
д) 
 б)
б)  в)
в) 
 д)
д) 
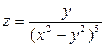 . Показать, что
. Показать, что 
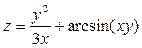 . Показать, что
. Показать, что 
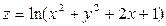 . Показать, что
. Показать, что 
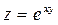 . Показать, что
. Показать, что 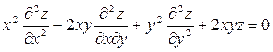
 . Показать, что
. Показать, что 
 . Показать, что
. Показать, что 
 . Показать, что
. Показать, что 
 . Показать, что
. Показать, что 
 . Показать, что
. Показать, что 
 . Показать, что
. Показать, что 
 . Показать, что
. Показать, что 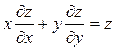
 . Показать, что
. Показать, что 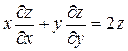
 . Показать, что
. Показать, что 
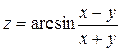 . Показать, что
. Показать, что 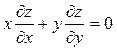
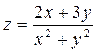 . Показать, что
. Показать, что 
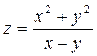 . Показать, что
. Показать, что 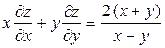
 . Показать, что
. Показать, что 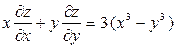
 . Показать, что
. Показать, что
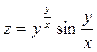 . Показать, что
. Показать, что 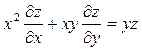
 . Показать, что
. Показать, что 
 точка
точка  и вектор
и вектор  . Найти: 1) grad z в точке А ; 2) производную в точке А по направлению вектора
. Найти: 1) grad z в точке А ; 2) производную в точке А по направлению вектора  .
. .
. .
. .
.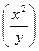 ; A(1; 2),
; A(1; 2),  .
. .
. .
. .
. .
.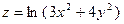







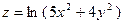



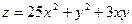

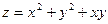




 ; б)
; б) 
 ; в)
; в)  ; г)
; г) 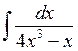 .
. б)
б)  в)
в)  ; г)
; г) 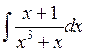 .
. ; б)
; б) 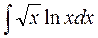 ; в)
; в)  ; г)
; г)  .
.  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.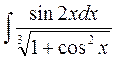 ; б)
; б)  ; в)
; в) 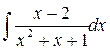 ; г)
; г)  .
. ; б)
; б)  ; в)
; в) 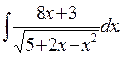 ; г)
; г)  .
. ; б)
; б) 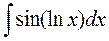 ; в)
; в)  ; г)
; г)  .
. б)
б)  в)
в)  г)
г) 
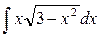 б)
б)  в)
в)  г)
г) 
 б)
б)  в)
в) 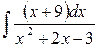 г)
г) 
 б)
б) 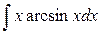 в)
в) 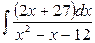 г)
г) 
 б)
б) 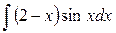 в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 
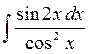 б)
б)  в)
в)  г)
г) 
 б)
б)  в)
в)  г)
г) 







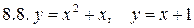
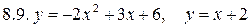

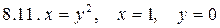






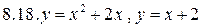


 б)
б) 
 б)
б) 
 б)
б) 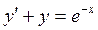
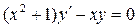 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
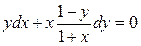 б)
б) 
 б)
б) 
 б)
б) 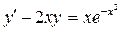

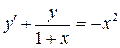
 б)
б) 
 б)
б) 
 б)
б) 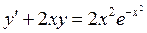
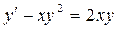 б)
б) 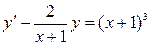
 б)
б) 
 б)
б) 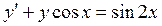
 б)
б) 
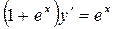 б)
б) 
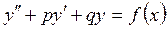 при данных начальных условиях
при данных начальных условиях  .
. ;
;  .
. ;
; 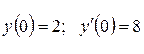 .
. ;
;  .
. ;
;  .
. ;
; 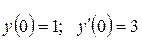 .
.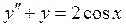 ;
;  .
. ;
;  .
.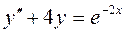 ;
;  .
.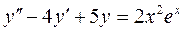 ;
;  .
.










 и
и  .
.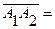 {1-2; 1-0; -4+3}={-1; 1; -1}
{1-2; 1-0; -4+3}={-1; 1; -1} {4-2; -2-0; 0+3}={2; -2; 3}
{4-2; -2-0; 0+3}={2; -2; 3}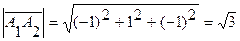 и
и 
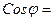

 {0-2; -1-0; 3-(-3)}={-2; -1; 6}
{0-2; -1-0; 3-(-3)}={-2; -1; 6}
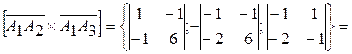 {5; 8; 3}
{5; 8; 3}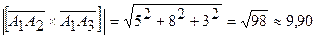
 (кв.ед.)
(кв.ед.)


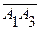 ,
,  объема параллелепипеда.
объема параллелепипеда.
 =
=  =
= 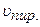 =
=  (куб.ед.)
(куб.ед.) Sосн
Sосн  H
H
 А4
А4
 {5; 8; 3}, и прямая А4О проходит через точку А4(4; -2; 0).
{5; 8; 3}, и прямая А4О проходит через точку А4(4; -2; 0). уравнение высоты.
уравнение высоты.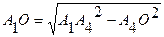
 , А4О=0,3
, А4О=0,3 (лин. ед.)
(лин. ед.) - уравнение плоскости А1А2А4
- уравнение плоскости А1А2А4
 - уравнение искомой плоскости.
- уравнение искомой плоскости.

 {5; 8; 3},
{5; 8; 3},  {1; 1; 0}
{1; 1; 0}


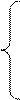



 и равен числу неизвестных системы, поэтому система совместна и имеет единственное решение.
и равен числу неизвестных системы, поэтому система совместна и имеет единственное решение.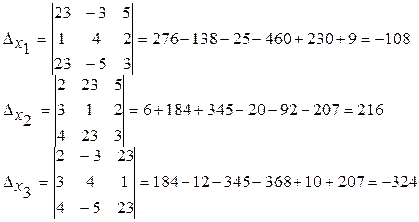
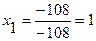 ,
,  ,
, 







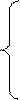





 .
. ,
, 
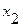 и
и  ,
, 
 ,
,  .
. .
. ;
; 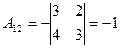 ;
;  ;
;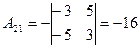 ;
; 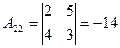 ;
; 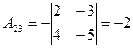 ;
; ;
; 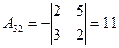 ;
; 
 .
.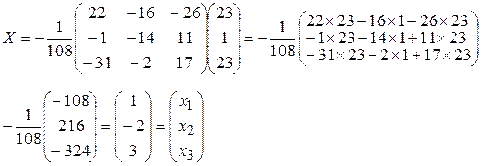
 при а) х0 = 2 б) х0 = 1 б) х0 = ¥
при а) х0 = 2 б) х0 = 1 б) х0 = ¥ 3)
3)  4)
4)