 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Экспериментальная часть. Изучение явления теплопроводности и измерение коэффициентов теплопроводности
Цель работы Изучение явления теплопроводности и измерение коэффициентов теплопроводности твердых диэлектриков. Теоретическая часть Теплопроводностью называют явление переноса теплоты от более нагретых тел или частей тела к менее нагретым. Основным законом теплопроводности является закон Фурье, утверждаюший, что плотность теплового потока
где c - коэффициент теплопроводности. Плотностьтеплового потока представляет собой вектор, направленный в сторону распространения тепловой энергии с модулем, равным количеству теплоты, переносимому за еденицу времени через площадку еденичной площади, расположенную перпендикулярно направлению распространения тепла. Таким образом, количество теплоты dQ, переносимое за время dt через площадку dS, перпендикулярную некой оси x, равно:
Физический смысл коэффициента теплопроводности заключается в том, что он численно равен количеству теплоты, переданному за единицу времени через единичную площадку в перпендикулярном ей направлении при единичном градиенте температуры. В случае идеального газа молекулярно-кинетическая теория для коэффициента теплопроводности дает следующее выражение:
где r - плотность газа; cV – удельная теплоемкость при постоянном объеме; l - средняя длина свободного пробега молекул;
В данной работе определяются коэффициенты теплопроводности двух твердых диэлектриков через известный через известный коэффициент теплопроводности третьего, эталонного тела. Пусть тела имеют форму достаточно тонких пластин, сложенных в стопу (см. рисунок). Считая, что температура изменяется только в направлении препендикулярном основанию стопы, то величина плотности теплового потока через каждую из пластин будет одинакова и равна:
где ci - коэффициент теплопровоности любой из трех пластин (i = 1, 2, 3). Разделим переменные:
и проинтегрируем уравнение в пределах толщины i-й пластины:
При небольших перепадах температур коэффициент теплопроводности можно считать постоянным, поэтому
т.е. получается система:
Таким образом, имея возможность измерить температуры на границах раздела пластин и зная коэффициент теплопроводности одной из них при известных толщинах, можно вычислить теплопроводности других:
Экспериментальная часть Схема установки
где 1 – термоблок; 2 – многоканальный цифровой термометр; 3-5 – квадратные пластины из разных диэлектриков; 6 и 7 – массивные плиты, сжимающие диэлектрики; 8 – нагревательная спираль; 9 – тонкие металлические прокладки, хорошо проводящие тепло; 10 – термопары. Результаты измерений d1 = 2,0 мм d2 = 1,0 мм d3 = 2,0 мм c2 = 0,174
Расчет погрешностей
Используя формулу
вычисляю абсолютные погрешности Dc1 и Dc3:
где DT1 = DT2 = DT3 = DT4 = 0,5 0C. c1 = 0,5336 ± 0,029; c1 = 0,3335 ± 0,014; Относительная погрешность рассчитывается по формуле:
e1 = 5.507 % e2 = 4.257 % Вывод: В ходе опыта было установлено, что коэффициент теплопроводности твердых диэлектриков зависит от толщины слоя диэлектрика и от разности температур в верхних и нижних слоях диэлектрика.
Поиск по сайту: |
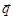 прямо пропорциональна градиенту температуры:
прямо пропорциональна градиенту температуры: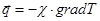 , (2.1)
, (2.1) , (2.2)
, (2.2)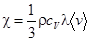 , (2.3)
, (2.3)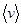 - средняя скорость молекул.
- средняя скорость молекул.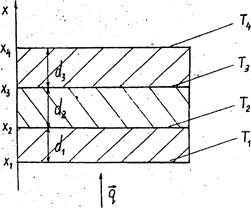 Расчет величины коэффициента теплопроводности для твердых диэлектриков показывает, что при достаточно высоких температурах он обратно пропорционален абсолютной температуре.
Расчет величины коэффициента теплопроводности для твердых диэлектриков показывает, что при достаточно высоких температурах он обратно пропорционален абсолютной температуре. , (2.4)
, (2.4)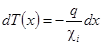 (2.5)
(2.5)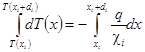 . (2.6)
. (2.6)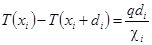 ; (2.7)
; (2.7)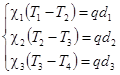 (2.8)
(2.8)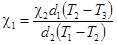
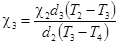 (2.9)
(2.9)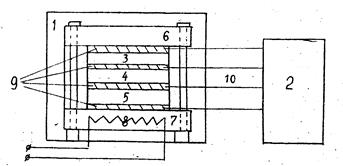
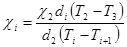 (3.1)
(3.1) (3.2)
(3.2)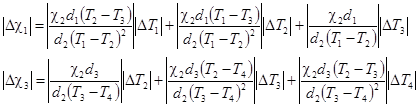 , (3.3)
, (3.3)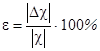 (3.4)
(3.4)