 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Период и частота гармонических колебаний
При колебаниях движения тела периодически повторяются. Промежуток времени Т, за который система совершает один полный цикл колебаний, называется периодом колебаний. Зная период, можно определить частоту колебаний, т.е. Число колебаний в единицу времени, например за секунду. Если одно колебание совершается за время Т, то число колебаний за секунду
Единица частоты называется Герцем (Гц) в честь немецкого физика Г. Герца.
Величина
Период колебаний равен:
Собственная частота колебаний математического маятника при малых углах отклонения нити от вертикали зависит от длины маятника и ускорения свободного падения:
Период же этих колебаний равен:
Билет 10. 1) Превращение энергии при гармонических колебаниях.
Полная механическая энергия при колебаниях тела, прикрепленного к пружине, равна сумме кинетической потенциальной энергии колебательной системы:
Кинетическая и потенциальная энергии периодически изменяются. Но полная механическая энергия изолированной системы, в которой отсутствуют силы сопротивления, сохраняется (согласно закону сохранения механической энергии) неизменной. Она равна либа потенциальной энергии в момент максимального отклонения от положения равновесия, либо же кинетической энергии в момент, когда тело проходит положение равновесия:
Энергия колеблющегося тела при отсутствии сил трения сохраняется неизменной. Если на тела системы действуют силы сопротивления, то колебания являются затухающими.
Билет 11. 1) Электромагнитные колебания. Свободные и вынужденные колебания. Колебательный контур. Превращение энергии при электромагнитном колебании.
Электромагнитные колебания — периодические или почти периодические изменения заряда, силы тока и напряжения. Обычно они происходят с очень большой частотой, значительно превышающей частоту механических колебаний. Поэтому для их наблюдения и исследования очень удобен электронный осциллограф. Свободными колебаниями называют колебания, которые возникают в системе после выведения ее из положения равновесия. В нашем случае колебательная система (конденсатор и катушка) выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалентна отклонению маятника от положения равновесия. Вынужденные колебания — колебания в цепи под действием внешней периодически изменяющейся электродвижущей силы. Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания, состоящая из конденсатора и катушки, присоединенной к его обкладкам.
Зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя. При этом конденсатор получит энергию
где По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока, которая определяется формулой:
где I – сила переменного тока; L – индуктивность катушки. Полная энергия W электромагнитного контура равна сумме энергий его магнитного и электрического полей:
В момент, когда конденсатор полностью разрядится (q=0), энергия электрического поля станет равной нулю. Энергия же магнитного поля тока, согласно закону сохранения энергии, будет максимальной. В этот момент сила тока также достигнет максимального значения
Допустим, что колебания незатухающие. Через промежутки времени, равные периоду колебаний, состояние системы в точности повторялось бы. Полная энергия при этому сохранялась бы неизменной, и ее значение в любой момент времени было бы равно максимальной энергии электрического поля или максимальной энергии магнитного поля:
Но в действительности потери энергии неизбежны.
В колебательном контуре энергия электрического поля заряженного конденсатора периодически переходит в энергию магнитного поля тока. При отсутствии сопротивления в контуре полная энергия электромагнитного поля остается неизменной.
Билет 12.
1) Аналогия между механическими и электромагнитными колебаниями.
Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями, например с колебаниями тела, закрепленного на пружине. Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин. Одинаковый характер изменения величин (механических и электрических) объясняется тем, что имеется аналогия в условиях, при которых возникают механические и электромагнитные колебания.
Электромагнитные и механические колебания имеют разную природу, но описываются одинаковыми уравнениями.
Билет 13. 1) Переменный электрический ток.
Свободные электромагнитные колебания в контуре быстро затухают, и поэтому они практически не используются. Напротив, незатухающие вынужденные колебания имеют огромное практическое значение. Переменный ток в осветительной сети квартиры, применяемый на заводах и фабриках и т. д., представляет собой не что иное, как вынужденные электромагнитные колебания. Сила тока и напряжение меняются со временем по гармоническому закону. Если напряжение на концах цепи меняется по гармоническому закону, то и напряженность электрического поля внутри проводников будет меняться гармонически. Эти гармонические изменения напряженности поля, в свою очередь, вызывают гармонические колебания скорости упорядоченного движения заряженных частиц и, следовательно, гармонические колебания силы тока. Но при изменении напряжения на концах цепи электрическое поле не меняется мгновенно во всей цепи. Изменения поля распространяются хотя и с очень большой, но не с бесконечно большой скоростью.
Билет 14. 1) Сила тока в цепи с резистором.
Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R. Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону:
Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:
В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством:
Билет 15. 1) Конденсатор в цепи переменного тока.
Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при это цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком. Переменный же ток может идти по цепи, содержащей конденсатор. Колебания силы тока опережают по фазе колебания напряжения на конденсаторе на Амплитуда силы тока равна:
Если ввести обозначение
и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим
Величину
Билет 16. 1) Катушка индуктивности в цепи переменного тока.
Индуктивность в цепи влияет на силу переменного тока. Максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. Из равенства Колебания напряжения на катушке опережают по фазе колебания силы тока на Амплитуда силы тока в катушке равна:
Если ввести обозначение
то получим:
Величину
Поиск по сайту: |

 — циклическая, или круговая частота колебаний. Циклическую частоту свободных колебаний называют собственной частотой колебательной системы.
— циклическая, или круговая частота колебаний. Циклическую частоту свободных колебаний называют собственной частотой колебательной системы.


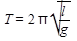


 ,
, — заряд конденсатора, а C – его электроемкость. Между обкладками конденсатора возникает разность потенциалов
— заряд конденсатора, а C – его электроемкость. Между обкладками конденсатора возникает разность потенциалов  .
. ,
,
 .
.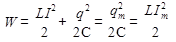

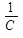







 .
.

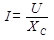
 , обратную произведению
, обратную произведению 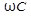 циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома. следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции
следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции  ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать:
) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: 
 .
. ,
,
 , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.