 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ. К решению этих задач следует приступить после изучения тем «Основные понятия и ⇐ ПредыдущаяСтр 4 из 4
К ЗАДАЧАМ 1-10 К решению этих задач следует приступить после изучения тем «Основные понятия и аксиомы статики», «Плоская система сходящихся сил», «Пара сил», «Плоская система произвольно расположенных сил». При этом необходимо усвоить понятия «проекция силы на ось», «момент силы относительно точки», научиться составлять уравнения равновесия для плоской системы сил. Во всех задачах определению подлежат опорные реакции тела, находящегося в равновесии под действием плоской системы произвольно расположенных сил. Реакции в стержнях направлены вдоль стержней, реакция гибкой связи направлена вдоль связи, реакции плоскости направлены перпендикулярно плоскости. Реакция шарнирно-подвижной опоры направлена по нормали к опорной поверхности шарнира. Реакцию шарнирно-неподвижной опоры принято представлять в виде двух составляющих реакций по осям координат. Вид применяемой системы уравнений равновесия может быть различным Σ МА = 0, Σ МВ = 0, Σ X = 0, Σ Y = 0. Три из этих уравнений используются для решения, одно из них – для проверки решения. При составлении уравнений следует помнить, что проекция силы на ось численно равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси ( [1], §7). Моментом силы относительно точки называется произведение модуля силы на плечо; плечом силы является перпендикуляр, опущенный из точки, относительно которой берется момент, на линию действия силы. Если при этом сила стремится повернуть тело по часовой стрелке, то ее момент считают положительным, если против часовой стрелки – отрицательным ( [1], §15). ПРИМЕР 1.Однородная балка, сила тяжести которой равна 2 кН, закреплена в точке А с помощью шарнирно-неподвижной опоры и опирается в точке В на ребро стены (рис. 7а). Найти реакции опор, если АС = 4м, ВС = 1м. Решение
Рис. 7 На балку действует одна активная сила – сила тяжести. В силу однородности балки сила тяжести приложена в ее середине, т. е. в точке D. Освободим балку от связей, приложив к ней вместо связей силы реакций ( рис. 7б). В точке А к балке надо приложить неизвестные две взаимно перпендикулярные силы RАх и RАу. В точке В балка опирается на ребро, следовательно, реакция RВ перпендикулярна балке АС (рис. 7 б). Сила тяжести вместе с реактивными силами представляет уравновешенную систему сил, произвольно расположенных в плоскости, для которой можно составить три независимых уравнения равновесия: два уравнения проекций и одно уравнение моментов. Составим уравнения равновесия: 1) Σ Fiх= 0. RАх – RВ cos 60º = 0. 2) Σ Fiy= 0. RАу – G + RВ cos 30 º=0. Для составления уравнения моментов в качестве центра моментов может быть выбрана точка плоскости, но для получения более простого уравнения нужно в качестве центра моментов выбрать ту точку, через которую проходит большее число неизвестных сил. 3)
Из (1) Из (2)
Для проверки правильности решения воспользуемся уравнением моментов относительно точки D.
Следовательно, задача решена правильно.
К ЗАДАЧАМ 11-20 К решению задач следует приступить после изучения темы « Центр тяжести» ( [1], §§ 23, 24). Центром тяжести тела называется центр параллельных сил тяжести всех элементарных частиц тела. Если тело имеет ось симметрии, то центр тяжести лежит на этой оси. Если тело имеет две оси симметрии, то центр тяжести находится на их пересечении. Центр тяжести может лежать и вне тела. Задачи решаются в следующей последовательности: 1.Составная фигура делится на простейшие геометрические фигуры, положения центра, тяжести которых известны (круг, прямоугольник, треугольник). 2.Выбирают оси координат, относительно которых берутся координаты центров тяжести каждой простейшей фигуры. 3.Вычисляют координаты центра тяжести сложной фигуры по формулам:
где
Если сечение имеет отверстия, площади отверстий вычитаются.
ПРИМЕР 2. Для тонкой однородной пластины, форма которой и размеры в миллиметрах заданы на рис.8, определить положение центра тяжести.
Рис. 8 Решение 1.Выбираем оси координат так, чтобы фигура была расположена в первом квадранте. 2. Разбиваем фигуру на три части: два прямоугольника I и II и круглое отверстие III. 3. Определяем координаты центров тяжести простейших фигур: х1= 25 мм , y1=15мм, х2= 40 мм , y2=50мм, ( х2 = 50 – 20/2 = 40 , y2 = 30 + 40/2 = 50), х3= 20 мм , y3=10мм. 4. Определяем площади составных частей: А 1 = 50 ∙ 30 = 1500 мм 2 , А 2 = 20 ∙ 40 = 800 мм 2 , А 3 = 3,14 ∙ 52 /4 = - 19,6 мм 2.
Знак «минус» означает, что А 3 - площадь отверстия. 5. Вычисляем координаты центра тяжести всей фигуры:
6. Покажем положение центра тяжести всей фигуры на чертеже: х С = 30,3 мм; yС = 28,2мм.
К ЗАДАЧАМ 21-50
Приступить к решению этих задач следует после изучения основных положений раздела «Сопротивление материалов» ([1], §§28- 1). Для успешного решения задач необходимо получить четкое представление о методе сечения для определения внутренних силовых факторов, о видах нагружения бруса, напряжениях, условии прочности и видах расчетов на прочность. В общем случае нагружения тела внутренние силовые факторы, возникающие в поперечном сечении нагруженного бруса, включают в себя продольную Nz и поперечные силы Qxи Qy, а также крутящий Мz и изгибающие моменты Мx , Мy. Метод сечения складывается из нескольких последовательных действий: - рассекают тело мысленно плоскостью на две части; - отбрасывают одну часть; - заменяют действие отброшенной части внутренними силовыми факторами; - уравнения равновесия составляют для оставленной части и решают, определяя из них значения и направления внутренних силовых факторов. Для наглядного изображения распределения внутренних силовых факторов вдоль оси бруса строят диаграммы, называемые эпюрами. Численное значение внутренних сил, приходящихся на единицу площади поперечного сечения у какой-либо его точки, называется напряжением. Напряжение измеряют в паскалях (1Па=1Н/мм2), кратные единицы – мегапаскаль (1МПа = 106 Па = 1Н/мм2). С помощью метода сечений определяют значение и знак внутренних силовых факторов во всех случаях по длине бруса, строят их эпюры и отыскивают опасное сечение бруса. Внутренний силовой фактор в произвольном поперечном сечении бруса численно равен алгебраической сумме соответствующих нагрузок, действующих на оставленную для рассмотрения часть бруса. Установленное в статике для сил и моментов правило знаков при определении внутренних силовых факторов неприменимо. Для каждого вида внутренних силовых факторов устанавливается собственное правило знаков. При построении эпюры любого внутреннего силового фактора должно соблюдаться следующее общее правило, вытекающее из метода сечений: внутренний силовой фактор в сечении, в котором приложена соответствующая сосредоточенная нагрузка, изменяется «скачком» на значение этой нагрузки. По виду внутреннего силового фактора устанавливают вид напряжения, возникающего в точках опасного поперечного сечения, закон его распределения по сечению и вид геометрической характеристики прочности сечения. Расчетное напряжение определяют как отношение внутреннего силового фактора к геометрической характеристике прочности. По эпюре определяют опасное сечение бруса и производят расчет на прочность. Условием прочности при расчете по допускаемому напряжению называют неравенство: σ ≤ [σ] или τ ≤ [τ], где [σ] и [τ] - допускаемое напряжение, зависящее от механических характеристик материала бруса и принятого коэффициента запаса прочности; σ и τ - расчетное напряжение. Из условия прочности определяют требуемое значение искомой величины. К решению ЗАДАЧ 21-30следует приступить после изучения темы « Растяжение и сжатие» ( [1], гл. VII). Растяжением (сжатием) называют такой вид нагружения бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор - продольная сила N, численно равная в любом поперечном сечении алгебраической сумме внешних сил, действующих на оставленную часть бруса: N = ΣFi. Продольные силы N, соответствующие деформации растяжения (т.е. направленные от сечения или от объекта равновесия) считаются положительными, в противном случае они - отрицательные. Для определения нормальных напряжений σ в поперечных сечениях значение продольных сил необходимо разделить на площади соответствующих сечений: σ = N / А . Проверка прочности осуществляется по формуле: σ = N / А≤ [σ], где σ -наибольшее рабочее напряжение; [σ] –допускаемое напряжение для материала стержня. Превышение рабочего напряжения по сравнению с допускаемым не должно быть больше 5%. Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука: Δ l = N· l / ( А· Е)= σ·ℓ / E; где Е - модуль упругости материала бруса ( для стали принимают Е = 2 ∙ 105 МПа). Для бруса, имеющего несколько участков, отличающихся размерами поперечного сечения или величиной продольной силы, изменение длины всего бруса будет равно алгебраической сумме удлинений (укорочений) отдельных участков: Δ l = Σ Δ li.
ПРИМЕР 3. Для двухступенчатого стального бруса (рис. 9) построить эпюры продольных сил и нормальных напряжений. Проверить брус на прочность. Определить перемещение свободного конца бруса, приняв модуль продольной упругости Е = 2 ∙ 105 Н/мм2; F1 = 30кН; F2 = 38 кН; F3 = 42кН; А1 = 190 мм2; А2 = 310 мм2; [σ] = 160 МПа.
Рис.9
Решение 1.Отмечаем участки, как показано на рис.9а. 2.Определяем значение продольной силы N на участках бруса: N1 =0; NII = F1 = 30 кН; NIII = F1 = 30 кН; NIV = F1 – F2 = 30 – 38 = – 8 кН; NV = F1 – F2 – F3 = 30 – 38 – 42 = – 50 кН; Строим эпюру продольных сил (рис.9б). 3. Вычисляем значения нормальных напряжений: σI = N1 / А1 = 0; σII = N1I / А1 = 30·103/ 190 = 158 Н/мм2; σIII = N1II / А2 = 30·103/ 310 = 96,8 Н/мм2; σIV = N1V / А2 = – 8·103/ 310 = – 25,8 Н/мм2; σV = NV / А2 = – 50·103/ 310 = – 161 Н/мм2; Строим эпюру нормальных напряжений (рис. 9в). 4. Проверяем прочность наиболее нагруженного участка. Условие прочности при растяжении, сжатии - σ = N / А ≤ [σ]. Наибольшее абсолютное значение рабочего напряжения возникает в пределах пятого участка. σ = σV = 161 Н/мм2 = 161 МПа; 161 МПа > 160 МПа – имеет место перегрузка бруса, которая составляет:
5.Определяем перемещение свободного конца бруса: Δℓ = ΔℓI +ΔℓII +ΔℓIII+ ΔℓIV +ΔℓV; Δℓ = σ·ℓ / E; ΔℓI = σIℓ·I / E = 0; ΔℓII = σII·ℓII / E = 158 · 0,5 · 103 / 2·105 = 0,394 мм; ΔℓIII = σIII·ℓIII / E = 96,8 · 0,1 · 103 / 2·105 = 0,0484мм; ΔℓIV = σIV·ℓIV / E = – 25,8 · 0,4 · 103 / 2·105 = – 0,0516мм; ΔℓV = σV·ℓV / E = – 161 · 0,2 · 103 / 2·105 = – 0,161мм. Δℓ = 0,394 + 0,0484 – 0,0516 – 0,161 = 0,23 мм. Брус удлиняется на 0,23 мм. К решению ЗАДАЧ 31-40следует приступить после изучения темы «Кручение» ([1], гл. IX). Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент Мк. Крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних моментов, действующих на оставленную часть, Мк = Σ Мi ( имеется в виду, что плоскости действия всех внешних моментов перпендикулярны продольной оси бруса). Крутящий момент считают положительным, если внешний момент направлен по ходу часовой стрелки при взгляде со стороны проведенного сечения. Условие прочности при кручении: τк = Мк / Wp ≤ [τк ], где τк - рабочее напряжение, возникающее в брусе; Мк - крутящий момент на брусе; Wp- полярный момент сопротивления, зависящий от геометрических параметров бруса. Для круглого сечения можно принять Wp= 0,2 d 3 мм 3; [τк] - допускаемое напряжение при кручении, зависящее от материала элемента конструкции. ПРИМЕР 4. Определить диаметр вала (рис.10) в опасном сечении из условия прочности на кручение, если допускаемое напряжение на кручение [τк] =100 Н/мм2; передаваемые мощности на вал: Р1 = 8 кВт, Р2 = 4 кВт, Р3 = 3кВт, Р4 = 1 кВт. Вал вращается равномерно с угловой скоростью ω = 3 рад/с.
Рис. 10
Решение 1.Определяем вращающие моменты на шкивах: М1= Р1/ω = 8 ·103 / 3 =2666 Н·м, М2= Р2/ω = 4 ·103 / 3 =1333 Н·м, М3= Р3/ω = 3 ·103 / 3 =1000 Н·м, М4= Р4/ω = 1 ·103 / 3 =333 Н·м, здесь Р - в Вт, ω -в рад/с, М – в Н·м. Так как вал находится в равновесии, то 2.Строим эпюру крутящих моментов, разделив вал на участки. Границы участков – места приложения вращающих моментов. Используя метод сечения, определяем крутящие моменты на каждом участке: Мк1 = М к5 = 0, Мк2 = – М2 = – 1333 Н·м, Мк3 = – М2 – М4 = – 1333 –333 = – 1666 Н·м , Мк4 = – М2 – М4 + М1 = – 1333 –333 + 2666 = 1000 Н·м, или Мк4 = М3 = 1000 Н·м. Из эпюры видно, что самый опасный участок – участок 3, где Мк3 = 1666 Н·м = 1,67 кН·м 3.Из условия прочности на кручение определяем диаметр вала в опасном сечении: Принимаем d=45мм. Остальные участки вала можно сделать меньших диаметров. К решению ЗАДАЧ 41-50следует приступить после изучения темы «Изгиб» ([1], гл. X). При изгибе в поперечных сечениях балок возникают два внутренних силовых фактора: изгибающий момент Ми и поперечная сила Q. При определении внутренних сил учитываются как активные внешние силы, действующие на балку, так и реакции связей. Поперечная сила, возникающая в каком-либо поперечном сечении, численно равна алгебраической сумме проекций на ось y внешних сил, действующих на балку по одну сторону от рассматриваемого сечения: Q = Σ Fн, а изгибающий момент – алгебраической сумме моментов внешних сил относительно центра тяжести сечения: Ми = Σ Мi. Поперечная сила считается положительной, если внешние силы слева от сечения направлены вверх, а справа от сечения – вниз. Поперечная сила считается отрицательной, если внешние силы слева от сечения направлены вниз, а справа от сечения – вверх. Изгибающий момент считают положительным, если внешняя сила, расположенная слева от сечения, вращает относительно центра тяжести сечения по ходу часовой стрелки, а справа от сечения – против хода часовой стрелки. В противном случае момент считают отрицательным.
Рис. 11 Балки выполняют постоянного по длине поперечного сечения, поэтому его размеры подбирают только для опасного сечения, имеющего по абсолютному значению максимальный изгибающий момент. Для определения опасного сечения строят эпюру изгибающих моментов, используя метод сечений. Условие прочности при изгибе: σ и = где σ и – рабочее напряжение, возникающее в балке; М и мах - максимальный изгибающий момент; Wx - осевой момент сопротивления изгиба зависит от геометрических параметров балки. Круг диаметром d: Wx = 0,1 d3; прямоугольник ( рис. 12): Wx =
Рис.12 ПРИМЕР 5. Для заданной двухопорной балки (рис. 13) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h,b,d) в форме прямоугольника или круга, приняв для прямоугольника h/b=1,5. Считать [σи] =160 МПа.
Решение 1. Определяем опорные реакции и проверяем их найденные значения (рис.13):
RB = ∑ МB = 0; – F1·AB + M2 – F2 ·BC – RD ·BD – M1= 0;
RD= Проверка: ∑ Fi = 0; – F1+ RB + F2 + RD = – 18 + 10 + 30– 22 = 0. 2. Делим балку на участки по характерным сечениям А, В, С, D (рис.13). 3. Определяем в характерных сечениях значения поперечной силы Qу и строим эпюру слева направо. QАпр = – F1 = – 18 кH; QВлев = – F1 = –18 кH; QВпр =–F1 + RB = – 18 + 10 = – 8кH; QСлев =–F1 + RB = – 18 + 10 = – 8кH; QСпр =–F1 + RB + F2 = – 18 + 10 +30 = 22 кH; QDлев =–F1 + RB + F2 = – 18 + 10 +30 = 22 кH.
Рис.13
4. Вычисляем в характерных сечениях значения изгибающего момента Мх и строим эпюру (рис.13). МА = 0; MВ = –F1·AB = –18·5 = – 90 кH·м; М Слев = – F1·AC + RВ·BC = –18·9 + 10·4 = –122 кH·м; М Спр = – F1·AC + RВ·BC + М2 = –18·9 + 10·4 + 10 = –112кH·м; М Dлев= – F1·AD+ RВ·BD+ М2+ F2 ·CD = –18·15 + 10·10 + 10 + 30·6 = 20 кH·м. 5.Подбираем размер сечения балки по двум вариантам: а) сечение ─ прямоугольник с заданным соотношением сторон; б) сечение ─ круг. Условие прочности на изгиб для материалов, одинаково сопротивляющихся растяжению и сжатию (сталь, дерево), имеет вид: σ мах= где Ммах ─ максимальный изгибающий момент; Wх ─
Вычисление размеров прямоугольного сечения: Wх = Используя формулу Wх= Wх= b= Диаметр круглого сечения находим, используя формулу Wх = d = Если требуется определить номер швеллера или двутавра Wх = 762000мм3762 см К ЗАДАЧАМ 51 – 60 К решению этих задач следует приступить после изучения тем: "Передачи вращательного движения" ([1],гл.XIX), "Зубчатые передачи" ([1],§§97,99,100,105,106), "Червячные передачи" ([1], гл. ХХII), "Ременные передачи" ([1], гл. ХХIII), "Цепные передачи" ([1], гл. ХХIV). В предлагаемых задачах требуется определить кинематические (ω) и силовые (Р, М) параметры для всех валов многоступенчатой передачи привода. Приступая к решению задачи, следует ознакомиться с ГОСТ 2.770-68 и 2.703-68 на условные обозначения элементов и правила выполнения кинематических схем. Валы и звенья нумеруются по направлению силового потока (направлению передачи движения) - от входного вала (вал двигателя) к выходному (рабочему) валу. Индекс в обозначениях параметров валов ω,Ри Мсоответствует номеру вала, а в обозначениях d и z- номеру насаженного на вал звена (колеса, шкива, звездочки и т.п.). Для общих параметров передачи - КПД η и передаточного отношения (числа) и - принята двойная индексация, соответствующая номерам валов передачи. Параметры любого последующего вала определяют через заданные параметры входного вала при условии, что известны КПД и передаточные отношения отдельных передач привода. При последовательном соединении общее передаточное отношение равно произведению передаточных отношений отдельных передач, то же - для КПД. В настоящем пособии для передаточного отношения ω1/ω2 и передаточного числа z2 /z1 принято единое обозначение и. Следует помнить, что индекс 1 относится к ведущему, а индекс 2 - к ведомому звену передачи. Ниже приведена таблица средних значений КПД некоторых передач (с учетом потерь в подшипниках). Таблица 6
ПРИМЕР 5. Для привода (рис.14), состоящего из электродвигателя мощностью Pдв = 4кВтс частотой вращения вала двигателя nдв = 1440 об/мин и двухступенчатой передачи с угловой скоростью выходного вала ωвых=12,5 рад/с, определить: 1. общий КПД привода, 2. общее передаточное отношение привода и передаточное число редуктора, 3. угловые скорости, мощности и вращающие моменты на валах.
Рис. 14 Решение Передача – двухступенчатая, понижающая, т.е. уменьшающая угловую скорость, так как в каждой ступени диаметр выходного звена больше диаметра входного. Первая ступень – закрытая цилиндрическая прямозубая передача (редуктор). Вторая ступень – открытая коническая зубчатая передача. 1. Определяем общий КПД передачи η общ = η1· η2 , где η1 = ηзцз =0,97, η2 = ηзко= 0,95, (таблица 6); тогда η общ = 0,97·0,95 = 0,92. 2. Определяем угловую скорость вала двигателя ωдв = π·nдв /30 =3,14· 1440 / 30 = 150 рад/с. Общее передаточное отношение привода: и13 = ωдв / ωвых = 150 / 12,5 = 12. Передаточное число конической передачи: и23 = z4/ z3 =54 /18 = 3. Общее передаточное отношение привода: и13 = и12 · и23 ; откуда передаточное число редуктора: и12 = и13 / и23 = 12 / 3 = 4. 3.Определяем угловые скорости на валах привода: ω1 = ωдв = 150 рад/с;ω3 =ωвых = 12,5 рад/с; и12 = ω1/ ω2, отсюда ω2 = ω1 / и12 = 150 / 4 = 37,5 рад/с. Мощность на валах: P1 = Pдв = 4 кВт; P2 = P1 η1 = 4 · 0,97 = 3,88 кВт; P3= P2 η2 = 3,88 · 0,95 = 3,68 кВт; или P3 = P1 ηобщ = 4 · 0,92 = 3,68 кВт; Вращающие моменты на валах привода: М1 = P1 / ω1 = 4 · 103 / 150 = 26,7 Н· м; М2 = P2 / ω2 = 3,88 · 103 / 37,5 = 103,46 Н· м; М3 = P3 / ω3 =3,68 · 103 / 12,5 = 294,4 Н· м, где Р - в Вт, ω - врад/с,М - в Н· м. В понижающих передачах понижение угловых скоростей валов сопровождается соответствующим повышением вращающих моментов. Мощности на валах снижаются незначительно вследствие потерь на трение в подшипниках и при взаимодействии звеньев.
Приложение 1
Поиск по сайту: |



 где
где 


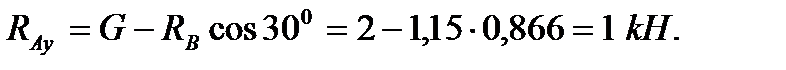
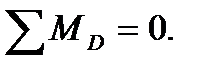



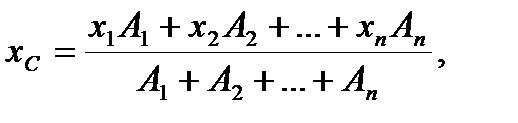

 - координаты центров тяжести простейших фигур;
- координаты центров тяжести простейших фигур; - площади простейших фигур.
- площади простейших фигур.


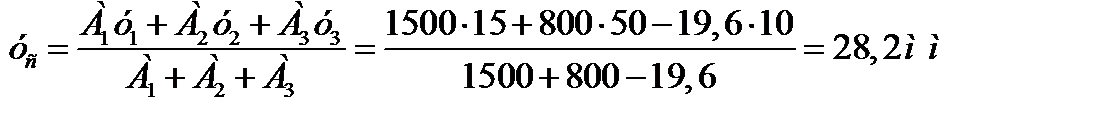

 , что вполне допустимо.
, что вполне допустимо.
 . М1 – М2 – М3 – М4 = 2666 – 1333 – 1000 – 333=0.
. М1 – М2 – М3 – М4 = 2666 – 1333 – 1000 – 333=0. где Wр = 0,2 d3 . Следовательно
где Wр = 0,2 d3 . Следовательно .
.
 ≤ [σи],
≤ [σи], ; квадрат со стороной а: Wx =
; квадрат со стороной а: Wx =  .
.
 =
=  = 10 кН .
= 10 кН . = – 22кН.
= – 22кН. =
=  = 762000 мм
= 762000 мм  .
.
 =
=  ,
, =
=  = 102 ·
= 102 ·  = 127 мм, h = 1,5·127 = 190мм.
= 127 мм, h = 1,5·127 = 190мм. ,
, =
=  = 196 мм.
= 196 мм. 