Алгоритм использующий Z-буфер

Впервые был предложен Кэтмулом. Для работы алгоритма, наряду с буфером кадра (цвета), необходим, совпадающий с ним по размерам, буфер глубины или Z-буфер. Отличительной особенностью алгоритма является его простота. Алгоритм работает в пространстве изображения. Основные шаги алгоритма следующие:

• заполнить буфер кадра фоновым значением интенсивности или цвета, z-буфер заполнить минимальным значением z для сцены. Если необходимо то удалить не лицевые грани;
• растеризовать каждый многоугольник сцены (порядок произволен);
• для каждой точки многоугольника с координатами (x, y) вычислить ее глубину z(x, у);
• сравнить полученную глубину z(x, у) со значением Z буфера, хранящимся в позиции (x, у);
• если z(х, у) > Z буфер (х, у), то записать атрибут этого многоугольника (интенсивность, цвет и т. п.) в буфер кадра и заменить Z буфер( х, у) на z ( х, у);
• в противном случае никаких действий не производить;

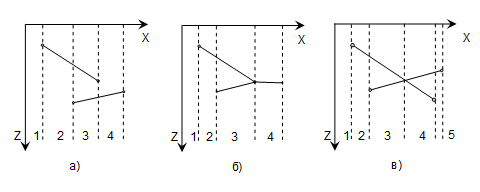
Рисунок 8.8 Схема работы алгоритма.

Схема, иллюстрирующая работу алгоритма приведена на рис. 8.8.

Кроме удаления невидимых линий алгоритм решает задачу об удалении невидимых поверхностей и делает тривиальной визуализацию пересечений сложных поверхностей. Сцены могут быть любой сложности. Поскольку размеры буфера кадра фиксированы, то оценка вычислительной сложности алгоритма не более чем линейна. Так как элементы сцены или картинки можно заносить в буфер кадра или в z-буфер в произвольном порядке, их не нужно тратить усилия на предварительную сортировку по приоритету глубины.

Алгоритм требует большого объема памяти, так как информацию о глубине нужно обрабатывать с достаточно большой точностью. Буфер цвета размером 1024х768х24 бит в комбинации с z-буфером глубиной 20 бит требуют около 5 мегабайт памяти. Уменьшение требуемой памяти достигается разбиением пространства изображения на несколько частей (квадратов или полос). Если использовать z -буфер размером в одну строку развертки то мы получим интересный алгоритм построчного сканирования . Поскольку каждый элемент сцены обрабатывается много раз, то сегментирование z-буфера, вообще говоря, приводит к увеличению времени, необходимого для обработки сцены. Однако сортировка на плоскости, позволяющая не обрабатывать все многоугольники в каждом из сегментов, значительно сокращает вычислительные затраты.

Другой недостаток алгоритма z-буфера состоит в сложности устранения лестничного эффекта, а также реализации эффектов прозрачности и просвечивания. Проблемы возникают из-за произвольного порядка заполнения буфера кадра. Поскольку алгоритм заносит пиксели в буфер кадра в произвольном порядке, то нелегко получить информацию, необходимую для методов устранения лестничного эффекта, основывающихся на предварительной фильтрации. Эти же причины приводят к ошибкам при реализации эффектов прозрачности и просвечивания.

4.11. ИНТЕРВАЛЬНЫЙ АЛГОРИТМ ПОСТРОЧНОГО СКАНИРОВАНИЯ

В алгоритме построчного сканирования с использованием z-буфера глубина многоугольника вычисляется для каждого пиксела на сканирующей строке. Количество вычислений глубины можно уменьшить, если использовать понятие интервалов, впервые введенных в алгоритме Ваткинса. На рис. 1, а показано пересечение многоугольников сцены со сканирующей плоскостью. Решение задачи удаления невидимых поверхностей сводится к выбору видимых отрезков в каждом из интервалов, полученных путем деления сканирующей строки проекциями точек пересечения ребер.

Из рисунка видно, что возможны только три варианта:

Рис. 8.9. Интервалы для построчного сканирования.

Интервал пуст, как, например, интервал 1 на рис. 8.9.а). – представляющие интервал пиксели имеют цвет фона.

Интервал содержит лишь один отрезок, как, например, интервалы 2 и 4 на рис. 8.9.а. - изображаются атрибуты многоугольника, соответствующего отрезку.

Интервал содержит несколько отрезков, как, например, интервал 3 на рис. 8.9.а). В этом случае вычисляется глубина каждого отрезка в интервале. Видимым будет отрезок с максимальным значением г. В этом интервале будут изображаться атрибуты видимого отрезка.

Если многоугольники не могут протыкать друг друга, то достаточно вычислять глубину каждого отрезка в интервале на одном из его концов. Если два отрезка касаются, но не проникают в концы интервала, то вычисление глубины производится в середине интервала, как показано на рис. 8.9 б) . Для интервала 3 вычисление глубины, проведенное на его правом конце, не позволяет принять определенное решение. Реализация вычисления глубины в центре интервала дает уже корректный результат.

Если многоугольники могут протыкать друг друга, то сканирующая строка делится не только проекциями точек пересечения ребер со сканирующей плоскостью, но и проекциями точек их по парного пересечения, как показано на рис. 8.9 в). Вычисление глубины в концевых точках таких интервалов будет давать неопределенные результаты. Поэтому здесь достаточно проводить вычисление глубины в середине каждого интервала. Используя более сложные методы порождения интервалов, можно сократить их число, а следовательно, и вычислительную трудоемкость

АЛГОРИТМ ВАРНОКА

В основу алгоритма Варнока легла гипотеза о том, что человек, при визуальном восприятии окружающей среды, уделяет основное внимание сложным объектам (несущим большое количество информации), а простые объекты или фрагменты изучаются с минимальными затратами. В ходе работы алгоритма изображение разбивается на отдельные части. Затем каждая часть получает оценку сложности. Если полученная часть достаточно проста, то мы можем принять решение о ее видимости, в противном случае продолжаем исследование, разбивая данную часть на подчасти. Таким образом, его можно охарактеризовать как рекурсивный алгоритм, работающий в пространстве изображения.

В оригинальной версии алгоритма исходное прямоугольное окно разбивается на четыре равные части. Простым является окно, если оно пусто или достигнут предел разрешения экрана. Пустое окно тривиально заполняется цветом фона, если алгоритм удаляет невидимые линии. При удалении невидимых поверхностей пустое окно дополнительно проверяется на охват многоугольниками сцены. При обнаружении нескольких охватывающих многоугольников окно заполняется цветом ближайшего к точке наблюдения.

Рисунок 8.10 Схема разбиения окна в алгоритме Варнока

При достижении предела разрешения в окне обычно оказывается один приксел (при устранении лесничного эффекта и в некоторых других случаях разбиение может продолжаться и далее. Цвет пикселя определяется взвешиванием окраски его частей). Для выяснения видимости окна так же находятся ближайший из охватывающих многоугольников и многоугольников границам которых принадлежит этот пиксел. Схема нескольких начальных разбиений окна при обработке алгоритмом Варнока простой сцены, представлена на рис 8.10. При первом разбиении подокно 1а оказалось пустым, остальные три подокна потребовали дальнейшего разбиения. Разбиение окна 1в (порядок рассмотрения подокон не важен. Мы просматриваем подокна слева направо, сверху вниз) также дает четыре подокна. Окно 2а пустое, оно может быть заполнено цветом фона. Окно 2b также требует разбиения. Основываясь на данной схеме разбиения окна, при разрешении экрана 1024*1024, мы достигаем предела разрешения экрана после десяти разбиений (1024 = 2¹⁰).

Рисунок 8.11 Разбиение окна на основе прямоугольной оболочки многоугольника.

Разработано большое количество модификаций данного алгоритма снижающих вычислительные затраты на обработку сцены. К основным направлениям развития алгоритма можно отнести следующие:

· Отступление от правила фиксированного деления окна пополам. Обработка изображения происходит эффективнее, если положение линий раздела окна зависит от его содержания. Например, окно разделяется на основе прямоугольной охватывающей оболочки находящегося в нем многоугольника, как это показано на рис.8.11;

· Расширение понятия простого содержимого окна (для него принимается решение о видимости без подразбиений). Для этого, рассматриваются возможные расположение многоугольника относительно окна и вводятся понятия внутреннего, внешнего, пересекающего и охватывающего многоугольника. На основе этих понятий вводятся правила обработки окон с простым содержанием. Примером может служить следующее правило: если в окне находится только один внутренний многоугольник, и у окна нет охватывающих многоугольников то площадь окна вне многоугольника закрашивается цветом фона а сам многоугольник заполняется соответствующим ему цветом;

· Отступление от разбиения окна на прямоугольники. Примером алгоритма, полученного при работе в данном направлении служит рассматриваемый далее алгоритм Вейлера-Азертона.

АЛГОРИТМ ВЕЙЛЕРА—АЗЕРТОНА

Для достижения необходимой точности алгоритм работает в объектном пространстве. Поскольку выходом являются многоугольники, то алгоритм можно легко использовать для удаления как невидимых линий, так и невидимых поверхностей. Алгоритм включает в себя четыре шага.

· Предварительная сортировка по глубине (по Zmax).

· Сортировка многоугольников на плоскости.

· Удаление многоугольников, экранированных многоугольником, ближайшим к точке наблюдения.

· Если требуется, то рекурсивное подразбиение и окончательная сортировка, для устранения всех неопределенностей.

Предварительная сортировка по глубине нужна для формирования списка приблизительных приоритетов. Точка наблюдения считается расположенной в бесконечности на положительной полуоси z. Ближайшим к ней и первым в списке будет многоугольник, который обладает вершиной с максимальной координатой Z.

Рисунок 8.12. Тестовый пример.

В качестве отсекающего многоугольника используется копия первого многоугольника из предварительного списка приоритетов по глубине. Вводятся два списка: внутренний и внешний На основе сортировки на плоскости все многоугольники отсекаются по границам отсекающего многоугольника. Сортировка на плоскости или ху–сортировка это двумерная операция пересечения проекций отсекающего и отсекаемого многоугольников. Части отсекаемых многоугольников, попадающие внутрь внутри отсекающего, заносятся во внутренний список. Многоугольники или части многоугольников оставшиеся вне отсекающего образуют внешний список. Результат первой сортировки сцены приведенной на рисунке 8.12 показан на рис. 8.13

Рисунок 8.13 Сортировка на плоскости.

Затем, сравниваются глубины всех вершин многоугольников из внутреннего списка с глубиной отсекающего многоугольника. Если глубина ни одной из этих вершин не будет больше Zmin отсекающего, то все многоугольники из внутреннего списка экранируются отсекающим многоугольником. Эти многоугольники удаляются, и изображается отсекающий многоугольник. Работа алгоритма затем продолжается с внешним списком. Если координата Z. какого-либомногоугольника из внутреннегосписка окажется больше, чем Zmin отсекающего, то такой многоугольник по крайней мере частично экранирует отсекающий многоугольник. Следовательно, результат предварительной сортировки по глубине ошибочен. Многоугольник, нарушивший порядок, выбирается новым отсекающим многоугольником. Отсечению подлежат многоугольники из внутреннего списка, причем старый отсекающий многоугольник теперь сам будет подвергнут отсечению новым отсекающим многоугольником. Подчеркнем, что новый отсекающий многоугольник является копией исходного многоугольника, а не его остатка после первого отсечения. Использование копии неотсеченного многоугольника позволяет минимизировать число разбиений.

Ненужное рекурсивное разбиение можно предотвратить, если создать список многоугольников, которые уже использовались как отсекающие. Тогда, если при рекурсивном разбиении текущий отсекающий многоугольник появляется в этом списке, значит, обнаружен циклически перекрывающийся многоугольник. Следовательно, не требуется никакого дополнительного разбиения.

Поиск по сайту: