 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Точный критерий Фишера ⇐ ПредыдущаяСтр 2 из 2
Точный тест Фишера – это тест статистической значимости, используемый в анализе категориальных данных, когда размеры выборки малы. Назван в честь его изобретателя, Р. A. Фишера, и является одним из класса точных тестов. Фишер разрабатывал тест после комментария от Muriel Bristol, которая утверждала, будто была в состоянии обнаружить, были ли чай или молоко добавлены сначала в ее чашку. Тест обычно используется, чтобы исследовать значимость взаимосвязи между двумя переменными в факторной таблице размерности 2 x 2 (таблице сопряженности признаков). Величина вероятности P теста вычисляется, как если бы значения на границах таблицы известны. Например, в случае с дегустацией чая, госпожа Bristol знает число чашек с каждым способом приготовления (молоко или чай сначала), поэтому якобы предоставляет правильное число угадываний в каждой категории. С большими выборками в этой ситуации может использоваться тест хи-квадрат. Однако, этот тест не является подходящим, когда математические ожидания значений в любой из ячеек таблицы с заданными границами оказывается ниже 10: вычисленное выборочное распределение испытуемой статистической величины только приблизительно равно теоретическому распределению хи-квадрат, и приближение неадекватно в этих условиях (которые возникают, когда размеры выборки малы, или данные очень неравноценно распределены среди ячеек таблицы). Тест Фишера, как следует из его названия, является точным, и поэтому может использоваться независимо от особенностей выборки. Для ручных вычислений тест выполним в только случае размерности факторных таблиц 2 x 2. Однако принцип теста может быть расширен на общий случай таблиц m x n, и некоторые статистические пакеты обеспечивают такие вычисления. Зависимые выборки. Используется критерий Мак-Нимара (Макнамары). Применяется если одна и та же выборка классифицируется по некоторому признаку дважды, но в различных условиях. Критерий Мак-Нимара Результаты записываются в виде таблицы сопряженности:
В данной таблице · a – количество объектов выборки, у которых и при первом, и при втором измерении было значение 1; · d – количество объектов выборки, у которых и при первом, и при втором измерении было значение 2; · b – количество объектов выборки, у которых при первом измерении было значение 1, а при втором – значение 2; · c – количество объектов выборки, у которых при первом измерении было значение 2, а при втором – значение 1. Гипотезы: · Н0– ОТСУТСВУЮТ ЗНАЧИМЫЕ РАЗЛИЧИЯ В СООТВЕТСТВ ИЗУЧАЕМОГО СВОЙСВА
· Н1– РАЗЛИЧНО В ДАННЫХ ВЫБОРКАХ
При проверке гипотезы различают 2 случая: 1) если 2) если Ограничения критерия:
-ИЗМЕНЕНИЯ В ДИХОТОМИЧЕСКОЙ ШКАЛЕ -ВЫБОРКИ ЗАВИСИМЫ (В НЕ РАВНО С) Пример. Школьный психолог проводит эксперимент по выявлению эффективных форм профориентационной работы. С этой целью он использует различные формы – лекции, беседы, экскурсии и т.п. Чтобы установить эффективность выбранной формы проводился опрос: «Нравится ли профессия экономиста?» у 20 учащихся до лекции об этой профессии и после лекции. Результаты приведены в таблице:
Можно ли считать данную форму профориентационной работы эффективной? Решение.
Пример. Исследуются различия в успешности решении двух разных по сложности мыслительных задач. Группа из 120 учащихся решала эти задачи. Результаты приведены в таблице:
Существуют ли статистически значимые различия? Решение.
Поиск по сайту: |
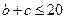 , то находится
, то находится  ,
,  . По таблице вероятностей для биномиального распределения находится Мэмп. Критическое значение для этого случая постоянно. Оно равно
. По таблице вероятностей для биномиального распределения находится Мэмп. Критическое значение для этого случая постоянно. Оно равно  :
:  . Нулевая гипотеза отвергается, если наблюдаемое значение меньше критического.
. Нулевая гипотеза отвергается, если наблюдаемое значение меньше критического. , то Мэмп.
, то Мэмп.  . Критическое значение находится по таблице критических точек распределения
. Критическое значение находится по таблице критических точек распределения  с числом степеней свободы f = 1 и уровнем значимости
с числом степеней свободы f = 1 и уровнем значимости