|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Какие используются измерительные шкалы?
На практике используются шкала порядка, шкала интервалов и шкала отношений. Шкала порядка представляет собой ранжированный ряд - упорядоченную последовательность размеров Q1< Q2< Q3<…< Qj<…, каждый из которых больше предыдущего, хотя сами размеры неизвестны. Если есть возможность опытным путем сравнить интересующий нас размер Qi, с одним из членов ранжированного ряда Qj, то экспериментальное решение неравенства Qi <> Qj, можно рассматривать как результат измерения, дающий некоторую количественную информацию о Qi. В соответствии с третьим постулатом метрологии решение о том, что i-ый размер меньше j-го либо больше или равен ему, носит случайный характер, т.е. выполняется с той или иной вероятностью, зависящей от силы неравенств. Решение (результат измерения) может оказаться ошибочным. При Qi>>Qj или Qi<<Qj вероятностью ошибки можно пренебречь. При Qi³Qj, Qi£Qj, и Qi»Qj с вероятностями ошибок нужно считаться. В таблице 2.4 приведен пример шкалы порядка Таблица 2.4 – Шкала Бофорта для измерения силы ветра
После двух или более измерений, т.е. после сравнения Qi, с несколькими членами ранжированного ряда, измерительная информация на шкале порядка может быть представлена в виде: Qi = Qi …Qj+1. Опорным (реперным) точкам j= 0, 1, 2, 3... на шкалах порядка принято ставить в соответствие баллы. С таким же успехом можно использовать буквенные обозначения или другие символы. Особенностью реперных шкал является то, что размеры Qj, образующие ранжированный ряд, как и интервалы между ними, неизвестны. Поэтому баллы ни складывать, ни вычитать, ни умножать, ни делить нельзя. На шкалах порядка не определены никакие математические операции. В то же время, если один размер на шкале порядка больше другого, а последний в свою очередь больше третьего, то и первый размер больше третьего. Или если хоть один из двух размеров больше третьего, то их сумма тоже больше третьего размера. Если из двух размеров каждый меньше третьего, то меньше третьего размера и их разность. Эти свойства транзитивности означают, что на шкалах порядка определены (т.е. могут выполняться) логические операции. Шкалы порядка являются наименее информативными из всех измерительных шкал. По ним не только нельзя определить, чему равен измеряемый размер Qi, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj. Наибольшее распространение шкалы порядка получили в областях, где к измерительной информации не предъявляется высоких требований. В промышленном производстве для измерений по шкалам порядка используются шаблоны. Шкала интервалов служит для представления результатов измерений, полученных посредством экспериментального сравнения i-го размера с j-ым по правилу Qi – Qj=DQ. Сами размеры Qi и Qj остаются при этом неизвестными. На рисунке 2. показано построение шкалы интервалов при j = 4. При выборе для сравнения 5-го, 6-го и больших размеров ноль на шкале интервалов DQ, получающийся при i = j, сместился бы выше, а при выборе 3-го, 2-го и меньших размеров - ниже показанного на рисунке. Таким образом, ноль на шкале интервалов не определен и зависит от выбора размера, с которым производится сравнение. Вследствие этого, по шкале интервалов можно установить, на сколько один размер больше другого, но нельзя сказать во сколько раз.
Рисунок 3 – Построение шкалы интервалов
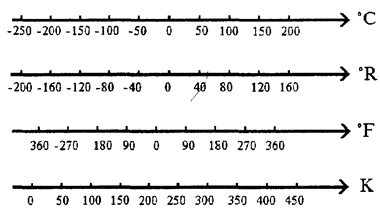
По шкалам интервалов измеряются время, расстояние (если не известно начало пути), температура и многие другие На рисунке 2.4 приведены, например, температурные шкалы Цельсия, Реомюра, Фаренгейта и Кельвина. Первая и последняя из них разбиты на интервалы, равный 0.01 разности температур кипения воды и таяния льда при атмосферном давлении. Шкалы Реомюра и Фаренгейта разбиты на градусы, равные соответственно 1/80 и 1/180 этого интервала. По шкалам Цельсия и Реомюра сравнение ведется с температурой таяния льда, по шкале Фаренгейта - с температурой смеси льда с солью и нашатырем, по шкале Кельвина - с температурой, при которой прекращается тепловое движение молекул. На градуированных шкалах интервалов откладываются не размеры DQi а значения DQi, интервалов. Шкалы интервалов являются более совершенными, чем шкалы порядка. На них определены аддитивные математические операции (сложение и вычитание), хотя и не определены мультипликативные (умножение и деление). Как следствие этого в экспериментальные данные, представленные на шкале интервалов, могут вноситься аддитивные поправки, в то время как использование поправочных множителей невозможно. Определить размер по шкале интервалов нельзя. Шкала отношенийслужит для представления результатов измерений, полученных посредством экспериментального сравнения неизвестного размера Qi = Q с размером Qj=[Q] по правилу Q/[Q] = q. Числовое значение q показывает, во сколько раз измеряемый размер Q больше размера [Q], принятого за единицу измерения, или на сколько единиц он больше нуля. На градуированных шкалах отношений откладываются не числовые значения q, а значения Q==q[Q] размеров Q. Градуированная шкала интервалов переходит в градуированную шкалу отношений при Qj®0; DQ®Qi=Q. На рисунке 2.4 шкала Кельвина представляет собой уже шкалу отношений. При практических измерениях на результат сравнения неизвестного размера Q с известным [Q] оказывает влияние множество (в том числе случайных) факторов. Поэтому на практике
где отсчет x не только не равен числовому значению q, но, в отличие от последнего, представляет собой случайное число. Показание Х=х[Q] и результат измерения Q=vX+Q, получающийся после внесения в показание поправок n и Q, являются, следовательно, также случайными и не могут быть представлены точками на числовой оси Q.
Рисунок 2.4 – Температурные шкалы Цельсия (°С), Реомюра (°R), Фаренгейта (°F) и Кельвина (К)
Шкала отношений является самой совершенной и наиболее распространенной из всех измерительных шкал. Это единственная шкала, по которой можно установить значение измеренного размера. На шкале отношений определены любые математические операции, что и позволяет вносить в показания, нанесенные на шкалу, мультипликативные и аддитивные поправки.
Поиск по сайту: |

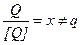 ,
,