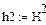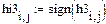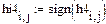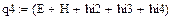|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
По дисциплине «Дискретная математика»
Курсовой работе Задания и методические указания к курсовой работе для студентов специальности – «Прикладная информатика» (очно - заочная форма обучения)
Курсовая работа (КР) состоит из расчетно-графического задания (РГЗ) и двух теоретических вопросов. Вариант РГЗ выбирается по сумме двух последних цифр зачетной книжки, первый теоретический вопрос по предпоследней, а второй – по последней цифре. КР оформляются на стандартных листах писчей бумаги с использованием текстового редактора и печатаются на принтере, кегль шрифта Time New Roman – 14. Отчет о РГР подшивается в папку. Отчет о РГР начинается со стандартного титульного листа на котором указывается (сверху - вниз): учебное заведение, кафедра, название и номер РГР, автор, дата выполнения, проверяющий с указанием ученой степени, ученого звания, фамилии и имени, отчества , дата проверки, город, год. После титульного листа следует содержание с указанием разделов и станиц. Далее идет текст отчета с рисунками, таблицами, расчетами, разбитый на соответствующие методическим указаниями разделы. За ним следуют ответы на теоретические вопросы. Затем следует список использованной литературы Задание 1 на расчетно-графическую работу №1 на тему: «Расчет числовых характеристик графов»
Задание на РГР формулируется следующим образом: «Найти основные числа графа G по данным, приведенным в таблице 5.1 для модели графа, представленной на рисунке 5.1: число вершин, число ребер, степени всех вершин, число компонент связности, цикломатическое число, хроматическое число, плотность и неплотность графа. Заданный на рис. 1 граф скопировать и преобразовать согласно варианта задания.
Рисунок 1 - Модель графа G
Таблица 1 - Данные для формирования графа G по вариантам
Рисунок 2 - Граф G 1.1 Расчет количества вершин n(G) графа G
Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:
1.2. Расчет количества ребер m(G) графа G
Расчет выполняется методом визуального анализа графа G. В итоге расчета имеем:
1.3Расчет степеней вершин δi графа G. Расчет выполняется методом визуального анализа графа G с целью определения количества ребер (дуг) инцидентных вершине xi. Результаты расчета сведены в таблицу .2.
Таблица 2 - Результаты расчета степеней вершин графа G
2. Расчет числа компонент связности æ(G)
Для расчета числа компонент связности графа G вычисляют матрицу достижимости ||Qp|| и определяют полные подграфы графа. Для построения матрицы достижимости удобно воспользоваться матрицей смежности графа G:
где ||1|| - единичная матрица (рисунок 3), ||H(xi)|| - матрица смежности графа G, ||Hp(xi)|| - матрица смежности графа G, возведенная в p-ую степень.
Рисунок 3 - Единичная матрица для графа G
Для возведения в степень матрицы смежности используют правило умножения булевых матриц. На рисунке 4 правило умножения булевых матриц прокомментировано графически.
Первая строка на первый столбец
Первая строка на второй столбец
Обозначения:
Рисунок 4 - Пример умножения булевых матриц 4х4
Если булевы операции заменить обычными алгебраическими операциями, нахождение матрицы достижимости сведётся к обычному пошаговому перемножению матриц.
Так как получившаяся матрица будет состоять не только из 0 и 1, то нужно воспользоваться функцией знака sign(x).
Данный алгоритм удобно реализовать используя математические пакеты, например MathCAD (смотри приложение 1) или написать программу на любом алгоритмическом языке. Программа на MathCAD приведена в файле «mat11new.xmcd». Рассмотренный в данных методических указаниях ниже следующий пример нужно заменить своим расчетом. Далее идет пример расчета: Построим матрицы смежности графа G (рисунок 5).
Рисунок 5 - Матрица смежности ||H|| графа G
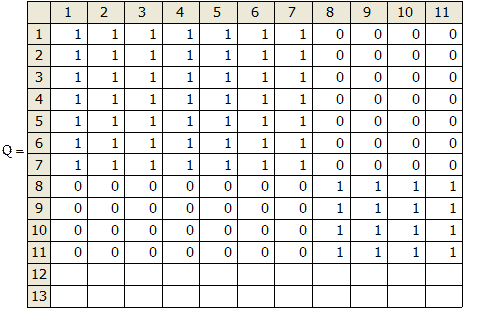
Получим матрицу достижимости ||Q|| графа G (рисунок 6).
Рисунок 6 - Матрица достижимости ||Q|| графа G
Рисунок 7 - Матрица ||H2|| графа G
Возведем матрицу смежности ||H|| в третью степень. Получим ||H3|| (рисунок 8).
Рисунок 8 - Матрица ||H3|| графа G Анализ матриц ||H2|| и ||H3|| показывает, что никаких изменений в ||H3|| по сравнению ||H2|| нет. Это значит, что процесс вычислений завершен. Матрица достижимости ||Q3|| (рисунок .9) рассчитывается следующим образом:
Рисунок 5.9 - Матрица ||Q3|| графа G
Поскольку матрица ||Q3|| содержит два блока: один – 3х3 элемента, другой – 6х6 элементов, то граф G содержит два связных подграфа:
где X1={x1,x2,x3}, X2={x4,x5,x6,x7,x8,x9}. Таким образом, для исходного графа G=<X,H> число компонент связности равно æ(G)=2.
Рассчитаем цикломатическое число графа G, т.е. наименьшее число ребер, удаление которых приведет к графу без циклов и петель. Расчет выполним по формуле:
В качестве примера удалим на графе G четыре ребра (1,3), (4,5), (5,6), (8,9). Получим граф на рисунке 10.
Рисунок 10 - Граф без циклов и петель
Рассчитаем хроматическое число графа G, т.е. наименьшее число красок при применении которых для раскраски вершин графа две любые смежные вершины графа G, не будут окрашены в один цвет. Для выполнения расчета воспользуемся двумя оценочными соотношениями. Одно из них задает левую границу для γ(G), min возможное значение γ(G), т.е. γmin(G):
1) полный n-вершинный граф имеет γmin(G)=n; 2) пустой граф имеет γmin(G)=1; 3) граф с циклом (т.е. хотя бы одним) четной длины имеет γmin(G)=2; 4) граф с циклом нечетной длины имеет γmin(G)=3; 5) граф-дерево имеет γmin(G)=2. Другое оценочное соотношение задает правую границу для γ(G), max необходимое значение γ(G), т.е. γmax(G):
Начинаем проверку с вычисления γmin(G). Поскольку в графе G есть цикл нечетной длины пробуем раскрасить граф тремя красками (рисунок 11).
Рисунок 11 - Раскраска графа G синей, желтой и красной красками
Вывод: трех красок, т.е. γmin(G)=3 оказалось достаточно:
Если бы трех красок оказалось недостаточно, следовало бы γmin(G) увеличить на единицу и повторить раскраску заново. И так далее, до получения желаемого результата. Однако таких красок не должно быть больше чем γmax(G).
Рассчитаем плотность графа G, т.е. наибольшее число вершин подграфа графа G, между всеми вершинами которого задано отношение смежности. Получим матрицы смежности ||H|| и достижимости ||Q|| графа G (рисунок 12).
Рисунок 12 - Матрицы ||H|| и ||Q|| графа G
В матрице || Q|| сформируем блоки, используя метод визуального анализа и перестановок строк (т.е. стоки меняются местами) и перестановок столбцов (т.е. столбцы меняются местами). В итоге получим матрицу ||Q|| на рисунке 13.
Рисунок 13 - Матрица || Q || с тремя выделенными блоками
Анализ матрицы || Q || на рисунке 13 показывает, что поскольку число блоков равно трем, то имеем три полных подграфа G с тремя вершинами в каждом (1-ый блок: 3х3, 2-ой блок: 3х3, 3-ий блок: 2х2). Иными словами, |Х`1|=3, |Х`2|=3, |Х`3|=2 (рисунок 14).
Рисунок 14 - Три подграфа графа G Обозначения: пунктиром выделены полные подграфы графа G.
Таким образом, имеем:
Другой алгоритм определения плотности графа приведен в монографии В.А. Горбатова «Фундаментальные основы дискретной математики» на странице 188. Алгоритм приведен в приложении 2. 6. Расчет неплотности ε(G) графа G (выполнять только на повышенную оценку) Рассмотрим плотность графа G, т.е. наибольшее число вершин пустого подграфа графа G между всеми вершинами которого нет отношений смежности. Построим обратный граф ┐G для графа G. Для этого получим матрицу || H || и обратную ей матрицу || ┐H || (рисунок 15).
Рисунок 15 - Матрицы смежности (слева-направо) графа G и графа ┐G
Строим матрицу достижимости графа ┐G и выполняем операцию перестановки строк и столбцов. Результаты показаны на рисунке 16.
Рисунок 16 - Матрицы достижимости ┐Qp графа ┐G Примечание: матрица на рисунке справа имеет блочную структуру.
На рисунке 17 показан обратный граф ┐G.
Рисунок 17 - Обратный граф ┐G
Анализ матрицы ┐Qp с блочной структурой на рисунке 16 показывает, что поскольку число блоков – три, то имеем три пустых подграфа графа G с тремя вершинами в каждом (рисунок 17): |Х`1|=3, |Х`2|=3, |Х`3|=3.
Рисунок 18 - Три пустых подграфа графа G
Таким образом имеем:
На этом расчеты числовых характеристик графа G закончены.
Задание 2. Теоретические вопросы Письменно ответить на вопросы:
Выбираются по предпоследней цифре зачетной книжки.
0. Основные характеристики графа.
Выбираются по последней цифре зачетной книжки.
Ответ на вопросы включает основные понятия и определения и объемом 2-3 страницы машинописного текста.
Поиск по сайту: |

 Пусть задан граф G (рисунок 2).
Пусть задан граф G (рисунок 2).




 - дизъюнкция (см. таблицу истинности по учебному пособию [4] );
- дизъюнкция (см. таблицу истинности по учебному пособию [4] ); - конъюнкция (см. таблицу истинности по учебному пособию [4])
- конъюнкция (см. таблицу истинности по учебному пособию [4])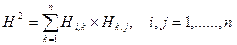
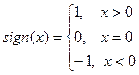

 .
.


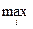
 .
.
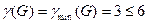 .
. (G) графа G
(G) графа G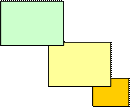 8
8


 .
.




 .
.