 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчетные свойства средней арифметической ⇐ ПредыдущаяСтр 2 из 2
1. Если индивидуальное значение признака уменьшить или увеличить в i раз, то среднее значение уменьшится или увеличиться в i раз. 2. Если все значения уменьшить(увеличить) на величину a ,то, среднее арифметическое уменьшится(увеличится) на величину а. 3. Если веса всех усредняемых вариантов уменьшить (увеличить) в к раз, то средняя арифметическая не изменится. Допустим величина А - это значение 1-го из центральных вариантов имеющего большую частоту. В качестве значения і выбирается интервал. Величина А назывется началом отсчета, а способ определения в этом случае называется способом момента. Допустим, что все значения мы уменьшим на величину А, затем уменьшим в і раз. Получаем новый вариационный ряд.
Тогда для получения действительной средней необходимо момент первого порядка умножить на і и прибавить А
Вид средней арифметической определяется характером взаимосвязи определяющего показателя с осредненным показателем.
Другие формы средних величин (средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя степенная.) Когда известно произведение x*f=w, то известна и сама средняя гармоническая. Причем разновидность ее – средняя гармоническая взвешенная:
Может быть простая:
Можем определить среднегармоническую взвешенность из средних величин:
Средняя геометрическая применятся в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, которые построены в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризуют средний коэффициент роста
Среднегеометрическое применяется для определения средних темпов изменения в рядах динамики и в рядах распределения.
Средняя квадратическая и кубическая применяются при расчетах показателей вариации, а также для определения среднего размера признака, выраженного в квадратных или кубических единицах:
Средняя квадратическая простая имеет вид:
Среднеквадратическая взвешенная:
Средняя кубическая простая:
Средняя кубическая взвешенная:
Можно вычислить среднюю прогрессивную – среднюю из лучших показателей.
Структурные средние. Структурная средняя используется для изучения внутреннего строения и структуры рядов распределения. Сюда относятся мода (Мо) и медиана (Ме). Мода – это значение случайной величины, встречающейся с наибольшей вероятностью. (в дискретном ряду это вариант, имеющий наибольшую частоту). Для интервальных рядов распределения с равными интервалами определяется по формуле:
Где:
Модальный интервал определяется по наибольшей частоте. Используется при изучении покупательского спроса и регистрации цен.
Медиана – это вариант, который находится в середине вариационного ряда. Чтоб найти медиану необходимо отыскать значение, которое находится в середине ряда. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к нахождению порядкового номера медианы. Номер Медины для нечетного объема вычисляется по формуле:
n - число членов ряда. Если четный объем, то номер медианы будет соответствовать средним двух центральных.
Где:
Медиана находит практическое применение в маркетинговой деятельности. Мода и медиана имеют значение конкретного варианта в вариационном ряду. Мода и медиана отличаются от значений средних, совпадают в случае если ряд симметричен. Используются для анализа формы распределения вариационного ряда. Аналогично медиане вычисляется значение признака, 3 делящего совокупность на 4 равные части – квартили, на 5 – квинтили, на 10 – децили, на 100 – перцентили. Вставка (графическое представление структурных средних).
(Вставка 4.5. Средняя величина как выражение закономерности.)
Поиск по сайту: |
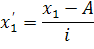

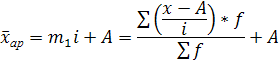
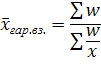








 – нижняя граница модального интервала;
– нижняя граница модального интервала; – модальный интервал
– модальный интервал ,
,  ,
, 
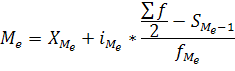
 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; - медианный интервал
- медианный интервал - половина от общего числа наблюдений;
- половина от общего числа наблюдений; – сумма наблюдений, которая накоплена до медианного интервала;
– сумма наблюдений, которая накоплена до медианного интервала; - число наблюдений в медианном интервале.
- число наблюдений в медианном интервале.